Lezioni con Mathematica

In questa pagina raccolgo alcune lezioni tenute con il supporto di Mathematica e scritte nella forma del notebook, forma che permette di accompagnare alle istruzioni di questo sofisticato programma e all'output di tipo grafico, numerico o simbolico da questo generato, pure un testo di spiegazione.
Ciascuna lezione consiste in un'esposizione dell'argomento in oggetto per cui il codice che via via viene proposto è strumentale a questo obiettivo didattico e la sua comprensione non è un prerequisito allo sviluppo dell'argomento.
Per chi invece fosse interessato anche alla comprensione delle istruzioni di Mathematica, troverà nella lezione sulla risoluzione del triangolo il codice più semplice mentre si utilizzano tecniche un po' più sofisticate in quella riguardante l'introduzione alle derivate (aggiornata recentemente alla versione 8 e affiancata al nuovo formato CDF) e nel pacchetto RettaFasci.m.

È evidente che per utilizzare pienamente questi notebook, anche a livello didattico, è necessario disporre di Mathematica almeno dalla versione 5. Si potranno in tal caso studiare situazioni diverse da quelle proposte e sperimentare modifiche e miglioramenti al codice nonché, avviare le diverse animazioni contenute. In alternativa si consiglia di

• prelevare il software gratuito CDF Player (106 Mb) che permette comunque la consultazione dei vari notebook, l'avvio delle animazioni e, nel caso di file in formato CDF una completa interattività: in alternativa si può prelevare una copia di valutazione di Mathematica. Si forniscono in alcuni casi le versioni:
• orientate alla stampa dei notebook (nel formato PDF) dove, per ovvie ragioni di spazio, sono stati ridotti al minimo i grafici di supporto alle animazioni. Si aggiungono infine
• una o più pagine d'ipertesto che simulano il layout di ciascun notebook così da poterle consultare on line con il browser.

La risoluzione del triangolo

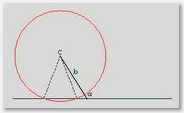
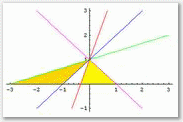
Si vogliono determinare tutti gli elementi caratterizzanti un triangolo qualsiasi, angoli e lati, supposto dato un loro sottoinsieme (per esempio, due lati e un angolo). Il problema, affrontato tradizionalmente in tutti i libri di testo quale applicazione dei teoremi fondamentali della trigonometria, viene qui riproposto in un notebook di Mathematica e in un foglio di lavoro di Derive.

A tal fine con i due file (di estensione .nb per Mathematica, .dfw per Derive), leggibili ovviamente disponendo dei relativi programmi oppure, per il solo Mathematica usando il gratuito MathReader, si distribuiscono pure le versioni PDF di ciascuno in modo da poter comunque facilmente accedere al contenuto. L'archivio compresso RisolTriangolo.zip contiene quindi quattro file, RisolTriangolo.nb, RisolTriangolo.dfw, RisolTriangolo.pdf e RisolTriangoloDerive.pdf.

Per la consultazione in linea della dispensa selezionare il link sottostante o la precedente immagine

Integrazione definita: le somme di Riemann

Questo notebook costituisce il testo di una lezione introduttiva all'integrazione definita dove si costruiscono, inizialmente con diverse tecniche, le somme di Riemann che approssimano l'area del trapezoide di una funzione continua definita in un intervallo [a,b]. Successivamente se ne studiano gli andamenti all'aumentare del numero n di suddivisioni.
In questa seconda parte si utilizzano le capacità di animazione di Mathematica mostrando, sia graficamente che numericamente, come le diverse somme tendano asintoticamente ad un medesimo valore. Si propone infine la definizione di integrale definito.

Per la consultazione in linea del notebook selezionare il link sottostante

In tal caso verrà caricato un file HTML con numerose immagini che simula il layout del notebook di Mathematica.
Volendo invece disporre del notebook per poi aprirlo in Mathematica o con MathReader prelevare il file compresso:

Si noti infine che, tranne nel caso di esecuzione del notebook entro Mathematica, in tutti gli altri file le animazioni sono state sostituite con delle terne riassuntive dei grafici ottenibili e ciò per contenere le dimensioni dei vari file.

Introduzione alle derivate

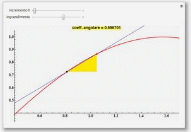
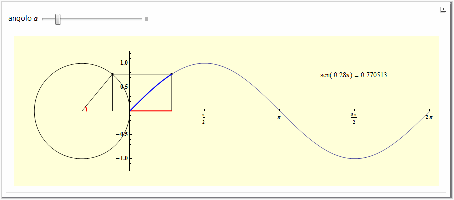
Lo scopo didattico di questo notebook di Mathematica è quello di proporre il significato geometrico di derivata in un punto di una funzione reale. Inizialmente si studiano delle funzioni in intorni di punti del loro dominio osservando come, per alcuni, all'aumentare dell'ingrandimento e quindi al diminuire dell'ampiezza dell'intervallo, il grafico tenda ad assumere andamenti approssimativamente rettilinei. Proposta la definizione di rapporto incrementale, si affronta quindi un'analisi di tipo grafico-geometrico del comportamento delle rette secanti e successivamente si passa al calcolo numerico dei loro coefficienti angolari o rapporti incrementali. Osservata la convergenza di tali rapporti al tendere allo zero dell'incremento, si fornisce la definizione formale di derivata in un punto. Si calcolano infine le derivate delle funzioni coinvolte nelle diverse fasi come limiti del rapporto incrementale.

Per la consultazione in linea della dispensa selezionare il link sottostante: l'immagine precedente dà invece accesso ad un'anteprima che, nel caso sia installato il CDF Player (106 Mb) con l'associato plugin potrà permettere di variare dinamicamente i parametri presenti già entro il proprio browser.

Il notebook originale è compreso nel file compresso seguente

mentre la versione nel formato CDF, consultabile in modo interattivo se sul proprio sistema è installato il gratuito CDF Player (106 Mb), si può prelevare dal link sottostante

Rette e fasci di rette

Questa serie di lezioni tratta inizialmente di alcune nozioni di base della geometria analitica e quindi introduce la retta nel piano cartesiano ottenendo dapprima la sua rappresentazione parametrica e quindi da questa deriva le rappresentazioni implicita ed esplicita. Successivamente si studiano i principali tipi di fasci di rette e le rispettive proprietà. Infine si propone un discreto numero esercizi di applicazione a partire dai più semplici a quelli più impegnativi.

Per rendere, per quanto possibile, la presentazione di questi argomenti sufficientemente snella ed essenziale così da favorire

• il riconoscimento delle nozioni teoriche coinvolte e la loro concatenazione e, nelle esercitazioni,
• l'identificazione dei metodi risolutivi piuttosto che i particolari del calcolo,

in tutti e tre i notebook che compongono questa serie di lezioni si fa uso delle funzioni contenute nel pacchetto RettaFasci.m redatto con lo scopo di ridurre gli aspetti di calcolo e grafici al minimo indispensabile. In tal modo le procedure di calcolo che comunemente vengono applicate nella geometria analitica della retta sono identificate da funzioni dal significato intuitivo immediato. Ciò potrebbe permettere all'insegnante che abbia una conoscenza anche minima di Mathematica, di preparare le proprie lezioni a carattere teorico o le esercitazioni focalizzandosi sugli aspetti più significativi delle nozioni e dei metodi favorendo l'attenzione degli allievi sulla loro struttura e coerenza complessiva.

Le nozioni trattate nel notebook Lezione1-Retta.nb, sono:

• coordinate del punto medio di un segmento
• distanza di due punti
• area del triangolo
• rappresentazione parametrica della retta
• rappresentazioni implicita ed esplicita
• grafici vari di rette.

Queste nozioni vengono dedotte a partire da precedenti conoscenze relative al calcolo vettoriale ma, ottenuta l'equazione di una retta per due punti, quanto segue (e cioè le rappresentazioni implicita ed esplicita della retta e il contenuto dei successivi notebook) viene affrontato sfruttando le usuali tecniche algebriche.

Le nozioni trattate nel notebook Lezione2-Retta.nb, sono:

• richiamo di alcune definizioni
• variazione del coefficiente angolare
• condizione di parallelismo tra rette in forma implicita
• condizione di perpendicolarità tra rette
• fasci di rette
• determinazione delle rette generatrici di un fascio e centro del fascio
• distanza punto–retta esplicita.

Il notebook Lezione3-EserciziRette.nb presenta invece

• 3 esercizi elementari
• 4 di primo livello
• 3 a carattere teorico
• 7 sui fasci di rette.

Infine in Help.nb si espone la terminologia utilizzata negli help delle singole funzioni. Segue quindi un elenco alfabetico delle funzioni implementate in RettaFasci.m e dei relativi help.

La precedente immagine e il link successivo permettono la consultazione di una pagina esemplificativa contenente alcune animazioni estratte dai vari notebook

Tutto il materiale prodotto sotto forma di notebook (estensione .nb), consultabile con Mathematica o con il MathReader, è contenuto nel file compresso:

La versione PDF dei vari notebook è contenuta invece in:

Definizione delle funzioni goniometriche e identità

In queste lezioni, suddivise in due notebook indipendenti, dopo aver introdotto la nozione di angolo orientato, si forniscono le definizioni delle funzioni goniometriche (seno, coseno e tangente) e le loro principali proprietà quali dominio, codominio, periodicità e grafico. Seguono poi le deduzioni delle numerose identità soddisfatte da tali funzioni e che le legano tra loro o che le associano a particolari combinazioni di angoli.

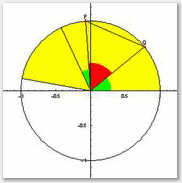
Nel primo notebook vengono utilizzate diverse animazioni sia per supportare a livello grafico la convenzione sugli angoli orientati sia per ottenere con opportune costruzioni i grafici di seno, coseno e tangente e per riconoscerne, in termini sintetici, le principali caratteristiche. In particolare si discute di:

• estensione delle ampiezze di un angolo,
• definizione delle funzioni seno, coseno e tangente,
• loro variazione e grafico,
• periodicità.

L'immagine precedente rimanda a una animazione interattiva se nel proprio sistema è installato il CDF Player e relativo plugin, statica altrimenti. I link successivi ad una pagina HTML che simula il notebook o, rispettivamente, alla sua traduzione in formato PDF. Per il notebook stesso (formato .nb) si veda sotto.

Il secondo notebook contiene le dimostrazioni delle più comuni identità goniometriche e per la deduzione di una di queste (formula di sottrazione per il coseno) si fa ancora uso di un'animazione grafica.
Volendo qui seguire un percorso deduttivo documentato che, iniziando da relazioni note le riscriva identicamente con trasformazioni di tipo algebrico, si è resa necessaria la stesura di alcune funzioni con caratteristiche peculiari e non sempre immediate. Da un punto di vista personale, tale lavoro costituisce quindi una piccola sperimentazione sulle modalità di calcolo di Mathematica e un'analisi su alcuni suoi limiti nella didattica. Le formule dimostrate sono:

• identità fondamentale,
• funzioni goniometriche in termini di una di esse,
• angoli associati,
• formule di addizione e sottrazione,
• formule di duplicazione,
• formule di bisezione,
• formule parametriche razionali,
• formule di Werner e prostaferesi.

Seguono i link ad una pagina HTML e alla versione PDF del notebook.

Infine, entrambi i notebook (formato .nb) sono contenuti nel file compresso sottostante.

---