Ritorna alla pagina di presentazione
Angoli orientati e definizione delle funzioni goniometriche
Presentazione
In questo notebook intendiamo dapprima introdurre la misura di un angolo orientato estendendola all'insieme dei reali e successivamente definiamo le funzioni goniometriche del seno, coseno e tangente studiandone i grafici e le periodicità.
Codice e funzioni utilizzate
Estensione delle ampiezze di un angolo
La misura dell'ampiezza di un angolo è comunemente espressa da un numero reale compreso nell'intervallo [0, 2π] se espresso in radianti oppure, se intesa in gradi, la misura appartiene all'intervallo [0°,360°]. Come per i segmenti anche per gli angoli è comunque possibile introdurre una orientazione o verso e quindi assegnare valori positivi o negativi all'ampiezza corrispondente.
Identificato quindi un lato dell'angolo (che è una semiretta) con il semiasse positivo delle x di un sistema cartesiano isometrico di origine O, potremo assegnare un verso all'angolo appena sia dato il secondo lato. Difatti, partendo dal semiasse positivo e muovendoci in verso antiorario fino ad incontrare l'altro lato, introduciamo la convenzione che associa all'ampiezza di quest'angolo un valore positivo. Se invece, sempre a partire dal semiasse positivo ci muoviamo in verso orario fino ad incontrare il secondo lato, l'ampiezza corrispondente dell'angolo in tal modo individuato verrà espressa da un valore negativo. Allora, per esempio, il seguente angolo è positivo
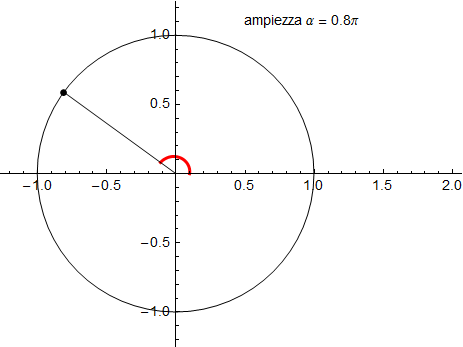
mentre quello rappresentato in fig. 2 è identificato da una misura dell'ampiezza di segno negativo: in termini geometrici tradizionali (cioè con ampiezze appartenenti agli intervalli ricordati sopra) la loro somma fornisce invece l'angolo giro cioè un'ampiezza di 360° oppure 2π.
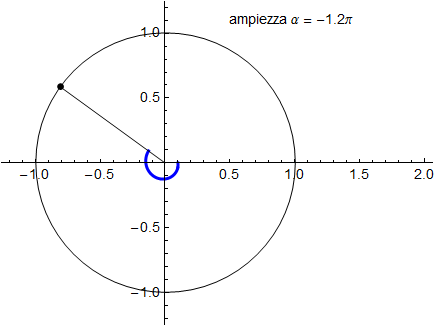
Come si vede, possiamo quindi individuare i due angoli nei quali viene suddiviso il piano, il primo (convesso in questo esempio) con una misura positiva, il secondo (nell'esempio, concavo) con una misura negativa. Poiché è possibile che il secondo lato dell'angolo ripassi più volte sul semiasse positivo delle ascisse ossia per il lato origine cioè ruoti attorno all'origine del sistema cartesiano, conveniamo di tener conto di tale eventualità nell'esprimere la misura dell'angolo in tal modo percorso. L'ampiezza dell'angolo potrà pertanto assumere qualsiasi valore positivo così come qualsiasi valore negativo. Difatti, ad ogni giro completo del secondo lato attorno all'origine O l'ampiezza dovrà aumentare di un valore pari a 2π (o 360°). L'animazione successiva mostra appunto come si debbano considerare angoli la cui misura sia maggiore di 2π
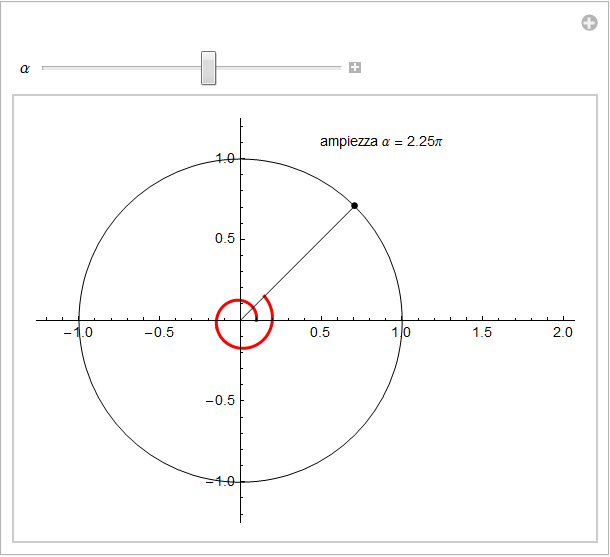
o minore di -2π.
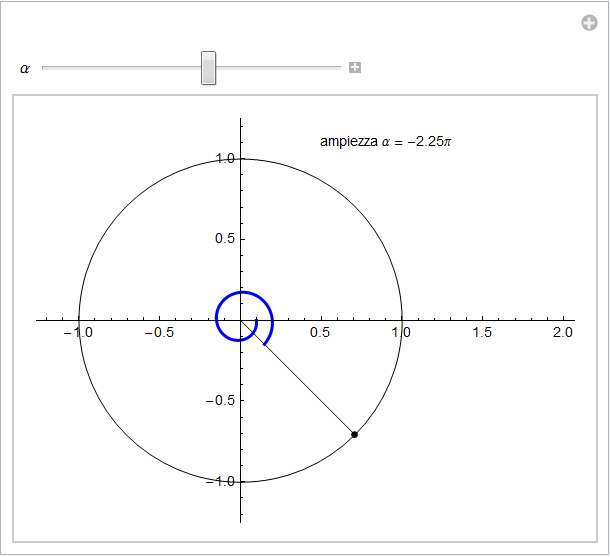
In definitiva, la convenzione appena introdotta ci permette di associare ad un qualsiasi numero reale α un angolo orientato ossia un angolo con lato origine sul semiasse positivo delle x di un sistema cartesiano e la cui ampiezza è espressa da un valore positivo o negativo a seconda che si debba ruotare in verso antiorario o orario per raggiungere il secondo lato ruotando, se necessario, anche più volte attorno all'origine. In termini un po' più formali abbiamo stabilito la funzione
che lega un numero reale ad un angolo orientato. Se al sistema cartesiano associamo pure una circonferenza γ di raggio dato qualsiasi e di centro nell'origine, il secondo lato determina un punto P (ed uno solo) di intersezione con γ cosicché in corrispondenza di un valore reale di α esiste un solo P ∈ γ. La corrispondenza qualitativa precedente si specifica quindi in
È immediato notare che tale funzione non può essere iniettiva: difatti è sufficiente riprendere il primo esempio (fig.1 e fig. 2) per vedere come al medesimo punto P (nelle figure evidenziato dal cerchietto nero) si possano associare già due valori distinti di α. Difatti in generale, se α individua un determinato angolo e quindi un punto P, viceversa questo stesso punto può essere individuato dall'insieme (numerabile) di valori α + 2kπ con k ∈ Z: ciascuno di questi valori differisce da α per un multiplo (positivo o negativo) di 2π, multiplo che descrive il numero di rotazioni complete attorno all'origine necessarie per "raggiungere" α + 2kπ a partire dallo stesso α.
Definizione della funzione seno di un angolo
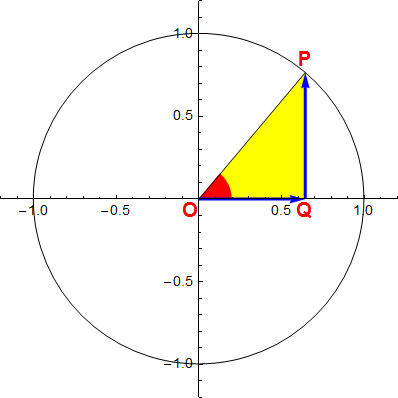
Ad un sistema cartesiano isometrico Oxy associamo quindi una circonferenza γ di raggio r assegnato e sia α l'ampiezza di un angolo qualsiasi (nelle figure verrà considerato r = 1: in tal caso la circonferenza viene identificata come la circonferenza goniometrica). Come detto, il secondo lato di tale angolo individua un punto P su γ: sia Q la proiezione sull'asse delle x di P, R quella sull'asse delle y.
Definiamo seno dell'angolo α il valore del rapporto
Definizione del seno di un angolo α
dove QP (fig. 3) rappresenta la misura del segmento orientato di estremi Q e P (o anche la componente del vettore OP sull’asse y). Se OP = 1 è pari anche all'ordinata del punto P. QP rappresenta quindi un valore che appartiene all'intervallo [-r, r]. OP è invece la lunghezza del segmento di estremi O e P oppure il modulo del vettore OP (oppure, come detto, il raggio r della circonferenza γ cui appartiene il punto P). OP è espresso pertanto da un numero positivo (r > 0) e al variare di P su γ rimane costante.
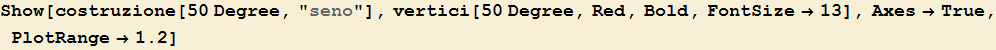
Variazione della funzione seno
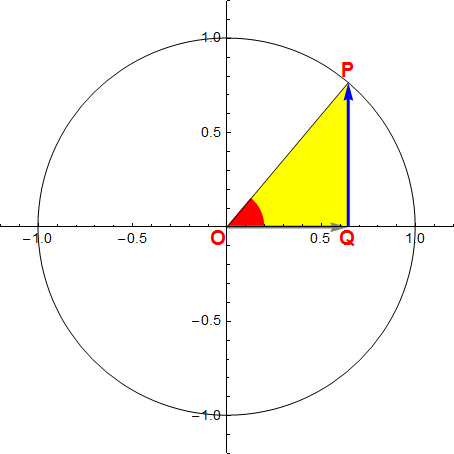
Per come abbiamo esteso l'insieme delle ampiezze di un angolo riusciamo ad associare ad ogni valore reale α un punto P sulla circonferenza e quindi siamo pure in grado di calcolare il rapporto tra QP e OP ossia il valore di sen(α). In tal modo disponiamo di una funzione che associa ad ogni α reale il valore y = sen(α).
Ci chiediamo ora quale siano le caratteristiche di tale funzione, in particolare il suo grafico e il suo codominio. Faremo pertanto variare α su un insieme di valori reali [0, 2π] analizzando, dapprima qualitativamente, le variazioni del segmento orientato QP e del suo rapporto con OP.
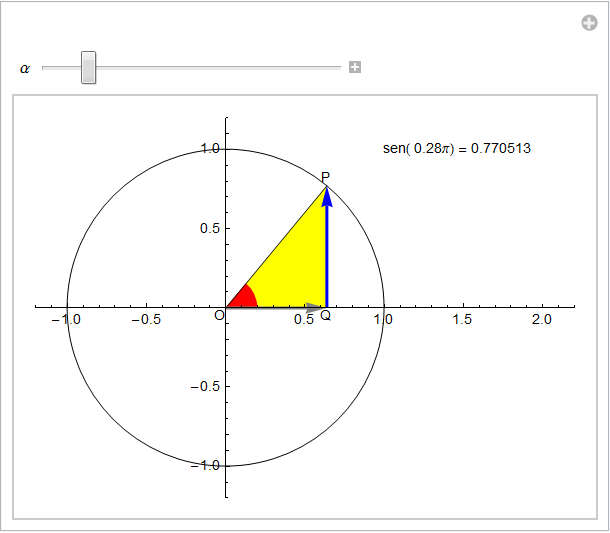
L'animazione ci fa comprendere come all'aumentare di α da 0 al valore di 
il seno aumenti raggiungendo il suo valore massimo, +1, in corrispondenza di 
. Per valori maggiori sen(α) diminuisce passando per il valore nullo quando α = π e assumendo valori negativi per 
. Infine raggiunto il valore minimo 
, la funzione ricomincia poi a crescere fino 2π. Il codominio appare quindi essere l'intervallo [-1, 1].
Grafico della funzione seno e periodicità
Per visualizzare un grafico della funzione seno al variare di α è comunque necessario un approccio più preciso. Riporteremo quindi i valori dell'angolo α sull'asse della variabile indipendente di un sistema cartesiano e, in corrispondenza, associamo all'ordinata il valore di sen(α). Per facilitare il riconoscimento del legame tra angolo e valore dell'ascissa riportiamo entrambi con lo stesso colore (rosso) mentre per mostrare che l'ordinata è effettivamente il valore del seno corrispondente tracciamo la circonferenza goniometrica (quindi OP = 1 e 
) traslata di una unità nel verso delle ascisse negative per non interferire con il grafico. Abbiamo pertanto
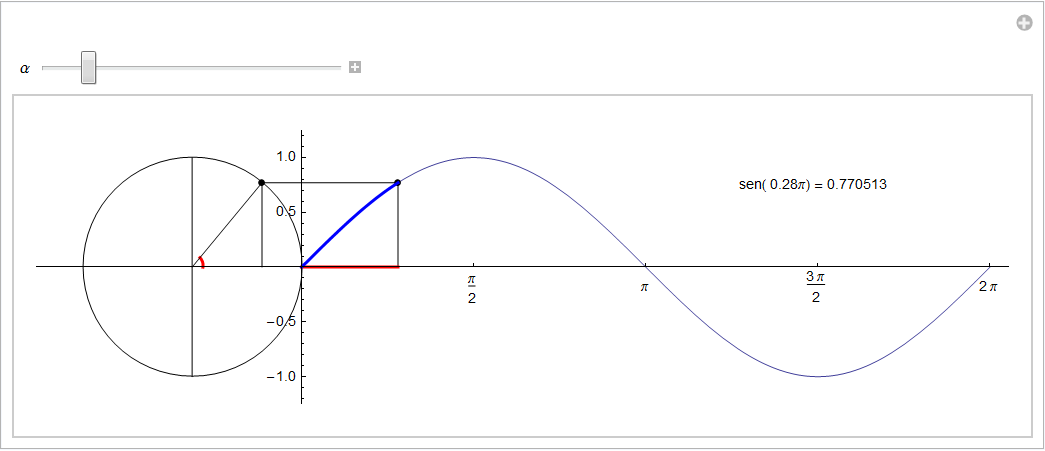
Il grafico emerge ora con immediatezza e ci permette di riconoscere con facilità gli intervalli dove sen(α) è crescente 
e dove invece risulta decrescente 
. Appaiono confermati pure i valori dell'angolo in corrispondenza dei quali il seno assume i valori massimo, 
, e minimo 
così come il codominio [-1, 1].
Possiamo infine dedurre un'altra importante proprietà della funzione seno e del suo grafico. Se estendiamo α a valori maggiori di 2π la configurazione geometrica del triangolo OQP (fig. 3) rimane inalterata e ciò evidentemente a seguito del modo con cui abbiamo esteso il dominio degli angoli. Di conseguenza la funzione sen(α) riprende gli stessi valori ma in corrispondenza di angoli diversi che differiscono dai precedenti per multipli di 2π. L'animazione seguente mostra quanto avviene per angoli nell'intervallo [0, 4π].
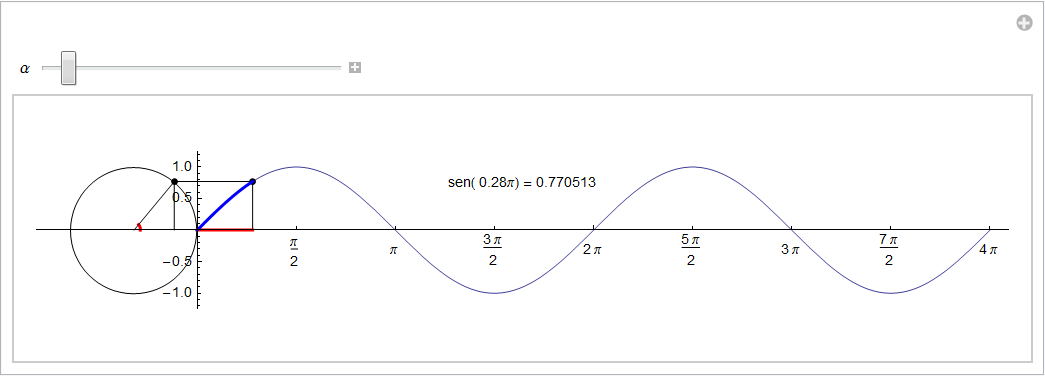
Funzioni con tale proprietà ossia tali da assumere i medesimi valori in corrispondenza di valori della variabile indipendente che differiscano per un certo valore T o suoi multipli interi, nel nostro caso T = 2π, verranno dette funzioni periodiche di periodo T. Per queste la definizione generale che si dà è
Definizione di funzione periodica
La funzione f è periodica con periodo T se e solo se
La figura 4 mette in evidenza che, pur essendo α ≠ α -2π ≠ α + 2π ecc. le uguaglianze
sono, per la funzione seno, certamente vere. Pertanto in generale, vale l'identità
e possiamo concludere che la funzione seno rientra nella definizione data sopra ed è quindi periodica con periodicità T = 2π.
Definizione della funzione coseno di un angolo
Per quanto visto circa la funzione seno, la definizione della seconda funzione goniometrica fondamentale cioè del coseno di un angolo, discende abbastanza naturale. Si pone pertanto
Definizione del coseno di un angolo α
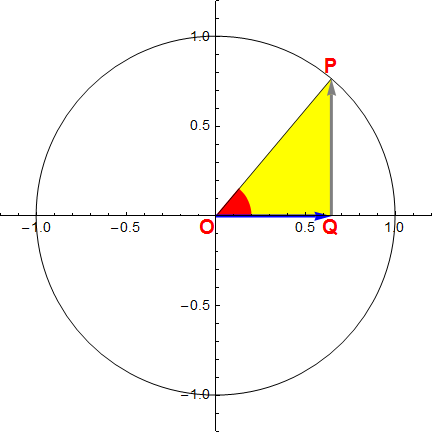
essendo OQ il segmento orientato (o componente "orizzontale" del vettore OP) che individua l'ascissa di P nella circonferenza γ di centro O e raggio OP (fig. 5).
Variazione del coseno
Un'analisi qualitativa dell'andamento della funzione y = cos(α) per α ∈ [0, 2π] basata sull'animazione seguente
permette di individuare già alcune interessanti caratteristiche.
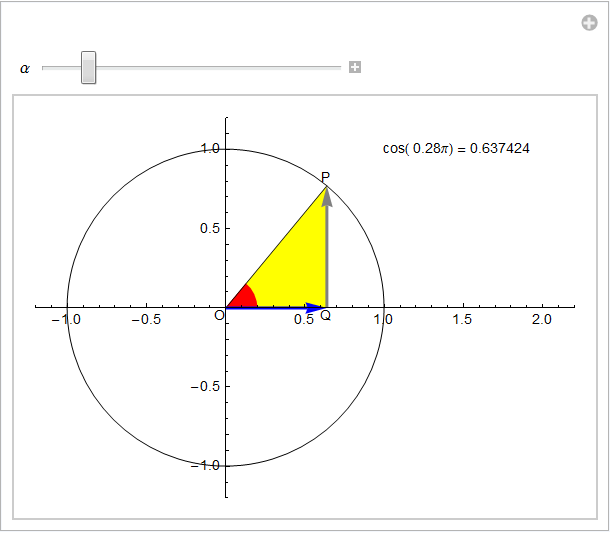
Riconosciamo difatti che tale funzione risulta positiva quando 
e in particolare assume il valore +1 in corrispondenza di α = 0 mentre vale -1 quando α = π. Questi rappresentano pure il valore massimo e, rispettivamente, minimo del codominio che pertanto è l'intervallo [-1, 1]. Appare inoltre decrescente in ]0, π[ e crescente in ]π, 2π[ mentre risulta 
.
Grafico della funzione coseno e periodicità
Per ottenere il grafico del coseno procediamo nello stesso modo seguito per il seno: trasliamo (ma solo a livello grafico) la circonferenza goniometrica di un'unità negativa sull'asse orizzontale onde non interferire con lo sviluppo del grafico e codifichiamo con lo stesso colore (rosso) l'angolo α percorso attorno all'origine e l'ascissa del punto (mobile) sul grafico del coseno. Poiché OP = 1 la definizione si riduce a 
cioè il coseno risulta pari all'ascissa del punto (di color nero) sulla circonferenza goniometrica e individuato dal secondo lato dell'angolo. Dato che intendiamo riportare in ordinata tale valore, eseguiamo una simmetria rispetto alla bisettrice del I e III quadrante, simmetria rappresentata nell'animazione seguente dal segmento tratteggiato: in tal modo il punto di color verde possiede ordinata pari a cos(α). Con tale costruzione il punto mobile che descrive il grafico ha coordinate (α, cos(α)): ne studiamo l'andamento per α ∈ [0, 2π].
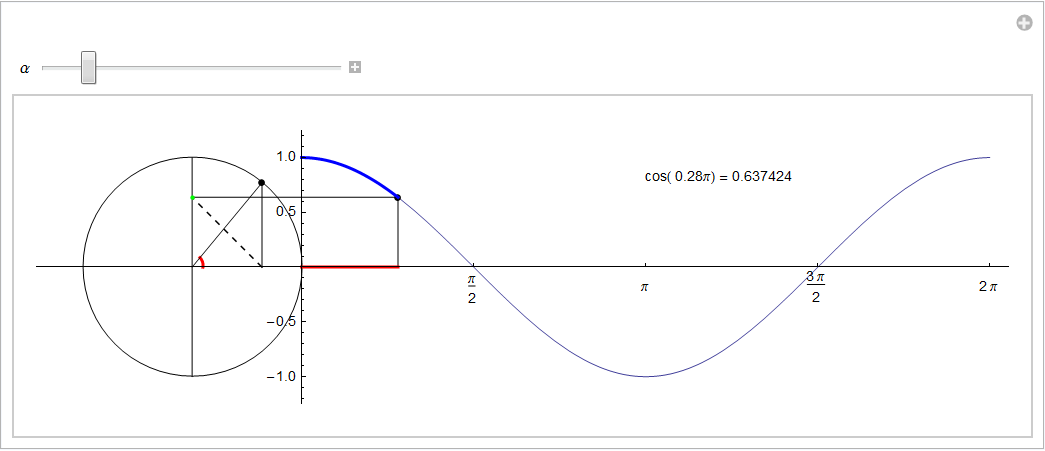
Per angoli esterni all'intervallo [0, 2π] la configurazione geometrica appena studiata si ripete inalterata suggerendo la periodicità pure della funzione coseno.
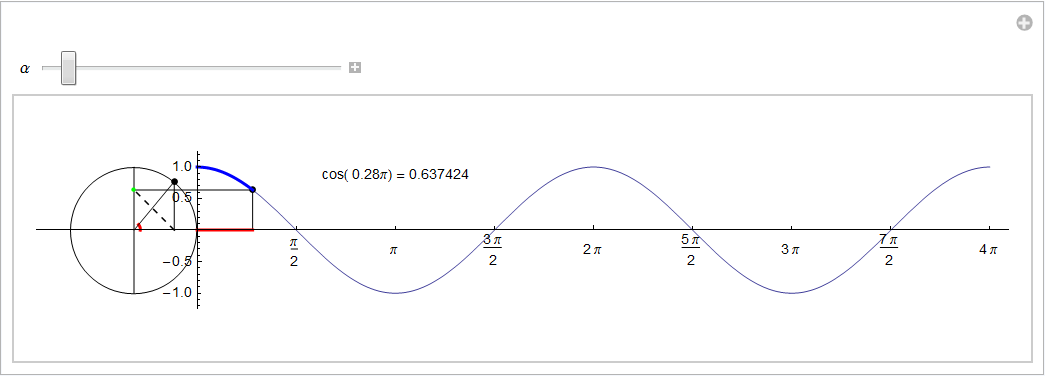
Valgono di conseguenza le seguenti identità (fig. 6)
casi particolari della più generale identità
e che stabilisce la periodicità della funzione coseno con periodo T = 2π.
Definizione della funzione tangente di un angolo e periodicità
Sempre in riferimento alla circonferenza γ associata ad un sistema cartesiano di origine O (fig. 7), definiamo la tangente di un angolo α come il rapporto
Definizione della tangente di un angolo α
dove entrambi i segmenti coinvolti vanno interpretati come segmenti orientati ossia come le componenti del vettore OP.
Da tale definizione discende immediatamente che la tangente non è definita quando OQ = 0: i valori di α che individuano le posizioni del punto P con ascissa nulla sono: 
che si possono riassumere in 
. Pertanto il dominio della funzione tangente è l'insieme
Poiché inoltre si può dividere numeratore e denominatore del secondo membro della definizione per OP, la tangente si può riscrivere identicamente come
non appena si siano tenute presenti le definizioni di sen(α) e cos(α). Ne segue che tg(α) risulta pure definita dal rapporto del seno e del coseno del medesimo angolo.
Periodicità
Una seconda importante proprietà discende sempre dalla definizione. Per dimostrarla analizziamo la configurazione geometrica che si presenta quando si considerino angoli che differiscono per π: per esempio, in figura 8, all'angolo α = 50° (in rosso) si associ l'angolo 50° + 180° = 230° (in verde).
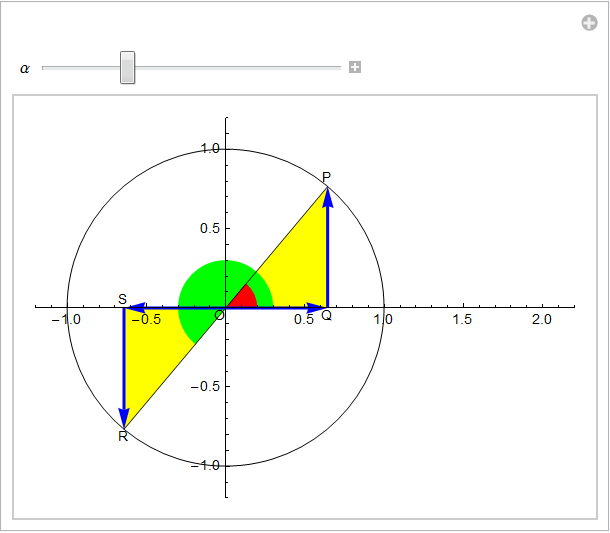
È evidente che i triangoli rettangoli △OQP e △OSR sono congruenti (∠ROS=∠POQ) ma che OS = -OQ e SR = -QP. Pertanto la tangente dell'angolo α + π che, per definizione, è
si può riscrivere come
Poiché tale relazione rimane valida qualsiasi sia l'angolo α potremo studiare la funzione tangente per valori appartenenti all'intervallo aperto 
e poi estenderla, in base ad essa, in 
. Ma più importante appaiono due osservazioni:
la prima consiste nel tener conto che ad α e agli angoli che differiscono da esso per multipli pari di π, α + 2kπ, si può associare la medesima configurazione (e ciò, come oramai sappiamo, equivale a k rotazioni complete attorno all'origine) per cui, di conseguenza, risulta tg(α) = tg(α + 2kπ).
Seconda osservazione: a α + π si possono associare i valori (α + π)+2kπ = α + (2k+1)π tali da differire da α per multipli dispari di π (difatti 2k + 1 è un numero dispari se k ∈ Z) e pure questi, per quanto dimostrato sopra, conducono ad una configurazione geometrica che fornisce lo stesso valore della tangente.
In definitiva qualsiasi sia il multiplo di π (pari o dispari) che lega α con α + kπ, risulta valida l'identità
Quest'ultima indentità stabilisce la periodicità della funzione tangente che pertanto, diversamente dal seno e coseno, possiede un periodo T = π.
Grafico della funzione tangente
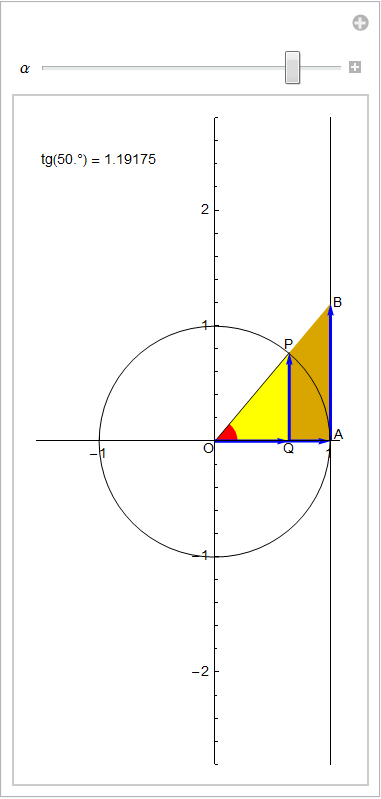
Per lo studio del grafico della tangente in funzione di α manca ancora un elemento che ci permetterà di disporre di un significato più intuitivo e diretto del rapporto dato nella definizione. Costruiamo a tale scopo la retta tangente nel punto A(1,0) alla circonferenza goniometrica (fig. 9) e prolunghiamo il secondo lato dell'angolo fino ad intersecare questa retta. Sia B il loro punto di intersezione.
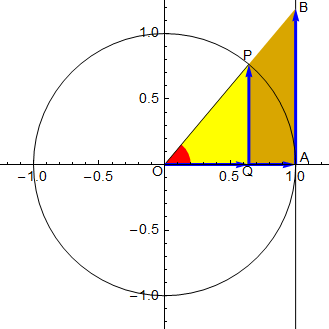
Data la similitudine tra △OQP∼△OAB e il fatto che OQ e OA siano concordi come QP e AB, risulta
dove si è considerato che nella circonferenza goniometrica OA = 1. Possiamo pertanto reinterpretare la tg(α) come la lunghezza del segmento orientato AB oppure anche come l'ordinata del punto B (oppure come la componente "verticale" del vettore OB). È ora immediato rappresentarci qualitativamente la variazione della tangente in funzione dell'angolo: a partire da 
(dove non è definita) all'aumentare di α aumenta pure la tangente che risulta un valore negativo per 
. È poi tg(0) = 0 e quindi la funzione assume valori positivi sempre maggiori quando α, aumentando, si avvicina a 
.
Sfruttando l'interpretazione precedente possiamo ottenere un grafico più preciso non appena si disponga in ascissa l'angolo α in modo del tutto analogo a quanto fatto per le funzioni seno e coseno. In ordinata poniamo quindi tg(α) cioè, geometricamente, riportiamo il segmento orientato AB. Per riconoscere più facilmente tale costruzione riportiamo in colore verde il punto B della precedente discussione e, in tratteggio, la retta tangente in (1,0) alla circonferenza goniometrica.
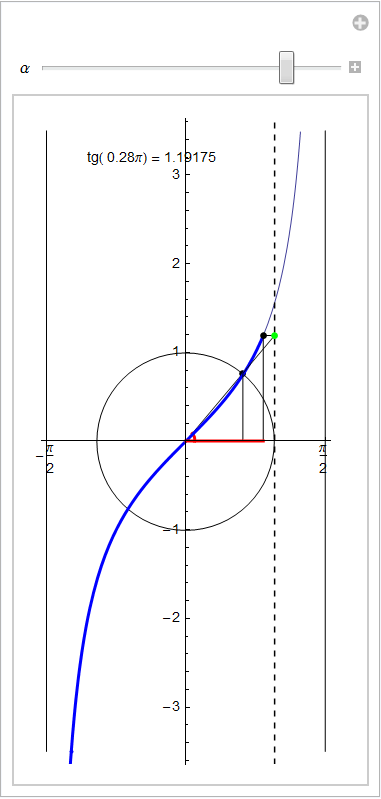
Appare quindi che il grafico della tangente tra 
è sempre crescente e possiede due asintoti verticali dati dalle rette 
. Osserviamo inoltre che, se α si avvicina a 
assumendo valori sempre inferiori di tale valore (o anche "da sinistra"), la tangente assume valori positivi sempre maggiori: esprimiamo tale andamento con la scrittura informale
Allo stesso modo se α si avvicina a 
essendo sempre maggiore di tale valore (o "da destra"), la tangente assume valori negativi sempre minori: informalmente esprimiamo ancora ciò con la scrittura
In base allo studio del grafico emerge pure il codominio di tale funzione: dato che il punto B (di color verde) può assumere qualsiasi posizione sulla retta tratteggiata, in corrispondenza la sua ordinata (cioè tg(α)) può assumere qualsiasi valore reale. Il codominio della funzione tangente coincide pertanto con R.
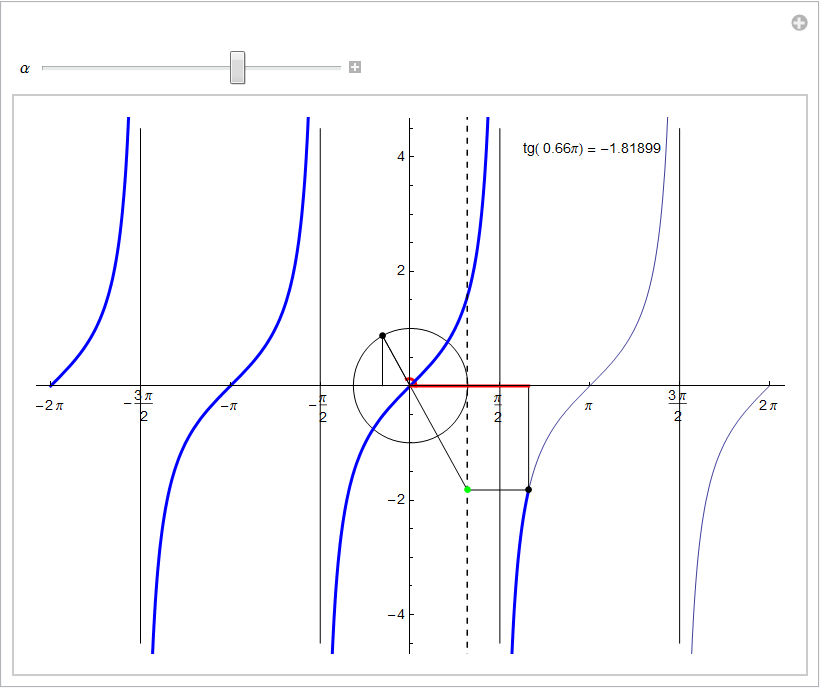
Visualizziamo infine il grafico della tangente in insiemi più estesi di 
così da rendere evidente la sua (già dimostrata) periodicità. Si tenga presente che in corrispondenza dei valori 
la funzione tangente non esiste (nella animazione seguente pertanto, gli asintoti 
non appartengono al grafico della tangente).
Ritorna alla pagina di presentazione
