![[Graphics:images/index_1.gif]](images/index_1.gif)
Ritorna alla pagina di presentazione
Nota
Lavoro proposto, in parte, in una classe quarta di liceo scientifico.
Vicenza, marzo 2003 (rivisto 19 marzo 2007)
Copyright © Lorenzo Roi (www.lorenzoroi.net)
La risoluzione del triangolo
Problema
Consideriamo un triangolo qualsiasi di vertici ABC aventi i lati di lunghezza a, b, c ed angoli α, β, γ (figura sottostante). Si vogliono determinare tutti i 6 parametri che caratterizzano il triangolo (lati a, b, c ed angoli α, β, γ), noto un sottoinsieme di essi. I parametri sono assunti essere tutti positivi e gli angoli verranno espressi in radianti ed inferiori a π. Generalmente si può determinare un unico triangolo specificando 3 dei 6 parametri benché in alcuni casi (si vedano i casi AAA e LLA) la configurazione possa essere ambigua.
![[Graphics:images/index_1.gif]](images/index_1.gif)
Possibili configurazioni
A seconda degli elementi assegnati, sono possibili 6 configurazioni: pertanto con L intenderemo assegnato un lato mentre con A è l'ampiezza di un angolo che è conosciuta. Le configurazioni sono:
AAA (Angolo-Angolo-Angolo). Sono specificati i 3 angoli di un triangolo. Sappiamo che in tal modo ne viene definita la forma ma esiste un'infinità di triangoli tutti simili tra di loro. Il problema quindi non possiede un'unica soluzione e risulta indeterminato data l'ambiguità sulla lunghezza dei lati.
AAL (Angolo-Angolo-Lato). Tale configurazione viene specificata assegnando due angoli e un lato non tra essi. Per esempio, potranno essere assegnati gli angoli α e β e il lato a (o b) ma non c. La configurazione per essere valida deve aver la somma dei due angoli minore di π: in tal caso essa ammette un'unica soluzione.
ALA (Angolo-Lato-Angolo). La configurazione consiste nel conoscere due angoli e il lato tra essi compreso (per esempio α, β e il lato c). Tale configurazione permette la determinazione di un'unica soluzione se la somma dei due angoli è minore di π.
LAL (Lato-Angolo-Lato). La configurazione coinvolge due lati e l'angolo compreso, per esempio i lati b, c e l'angolo α. Per tutti i valori dei parametri, la configurazione ammette un'unica soluzione.
LLL (Lato-Lato-Lato). Si specificano i tre lati di un triangolo. La soluzione è unica se viene rispettata la disuguaglianza triangolare ossia se la somma di due qualsiasi di essi è maggiore del terzo. Viceversa, se la lunghezza di un lato è maggiore o uguale della somma dei rimanenti non esiste alcun triangolo.
LLA (Lato-Lato-Angolo). Tale situazione dove sono assegnati due lati e un angolo non compreso, per esempio a, b e angolo α , sono ambigue e vanno trattate con attenzione. Gli esiti che si possono presentare sono diversi potendo esistere due insiemi di parametri possibili e conseguentemente due triangoli oppure un solo triangolo oppure, la configurazione può essere inconsistente e rendere impossibile l'esistenza di soluzioni.
Teoremi
Il processo per determinare l'intero insieme di parametri, data una particolare configurazione, viene indicato come la risoluzione del triangolo e coinvolge alcune conoscenze fondamentali sui triangoli. Queste sono:
- la somma degli angoli interni di un triangolo è π, ossia
![]()
- teorema dei seni. Si esprime come
![]()
- teorema del coseno o di Carnot:
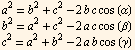
ed infine, la disuguaglianza triangolare
![]()
valida per qualsiasi permutazione dei lati a, b, c.
Implementazione
Funzioni di base
In base ai teoremi delineati sopra vengono qui definite alcune funzioni di base che permettono una scrittura più sintetica delle funzioni successive.
La prima LatoCarnot, fornisce la lunghezza di un lato utilizzando il teorema di Carnot: devono pertanto essere noti due lati e l'angolo compreso.
![]()
Nel caso che siano conosciuti due angoli ed il lato opposto ad uno di essi, in base al teorema dei seni si ottiene la lunghezza del lato opposto all'angolo rimanente. La funzione è
![]()
Sempre in base al teorema dei seni si può ottenere l'angolo opposto ad uno di due lati noti (per es. b e a) se risulta assegnato pure l'angolo opposto all'altro (per es. α). Dei due valori possibili per l'angolo (acuto o ottuso) questa funzione restituisce l'angolo acuto.
![]()
Analogamente, noti i tre lati si può ottenere l'angolo opposto a ciascuno (del primo lato inserito) con la funzione seguente, ancora basata sul teorema di Carnot.
![]()
Prime funzioni
Funzione AAA
Evidentemente dati i soli tre angoli di un ipotetico triangolo non è possibile determinarne univocamente uno. Infatti in tal modo esiste un'infinità di triangoli aventi gli angoli assegnati, tutti simili uno all'altro. Per poterne determinare uno va quindi dato almeno un lato per cui si ricade nel caso AAL oppure ALA.
Funzione LAL
La scrittura della funzione collegata alla configurazione LAL è immediata in quanto, per qualsiasi terna lato-angolo compreso-lato, si può ottenere il triangolo corrispondente. Il triangolo viene fornito dalla funzione LAL e da tutte le successive sotto forma di matrice di 3 righe e 2 colonne, dove la prima colonna dà gli angoli (in radianti) e la seconda le lunghezze dei lati corrispondenti (nella convenzione definita all'inizio). Inoltre, sia in questa che nelle funzioni successive, utilizziamo il comando di Mathematica Module: in tal modo possiamo definire della variabili locali che rendono più agevole la lettura e l'individuazione delle proprietà. Per esempio, in LAL, la variabile locale c mette in evidenza che il terzo lato si ottiene applicando il teorema di Carnot: analogamente per l'angolo α. Nel caso che l'angolo dato sia maggiore di π ovviamente il triangolo non esiste e la funzione restituisce la stringa NE (Non Esiste).
![LAL[a_, γ_, b_] := <br /> Module[{c, α ... ; ]](images/index_10.gif)
Funzione AAL
Pure la funzione AAL non presenta particolari difficoltà. Nel caso però che la somma dei due angoli dati sia maggiore o eguale a π non è possibile determinare il triangolo. In tal caso la funzione restituisce la stringa NE (Non Esiste). I lati rimanenti vengono calcolati applicando due volte il teorema dei seni come appare evidente dalla definizione delle due variabili locali, b e c. Come sottolineato negli esempi il primo angolo immesso è quello opposto al lato conosciuto ed inserito come terzo argomento della funzione.
![AAL[α_, β_, a_] := <br /> ... ; ]](images/index_11.gif)
Funzione ALA
Per il caso ALA, dove il lato assegnato è quello compreso tra i due angoli, va ancora rispettata la condizione α+β<π. In caso contrario non esiste il triangolo. I lati mancanti si ottengono ancora con il teorema dei seni.
![ALA[α_, c_, β_] := Module[{a, b}, If[α + β<π, ... ; ]](images/index_12.gif)
Funzione LLL
La realizzazione della funzione LLL implica un controllo sulla disuguaglianza triangolare. Difatti per esempio, un triangolo con un lato pari ad 1, un altro pari a 2 ed un terzo di lunghezza 10 non può esistere (si pensi a delle circonferenze di raggi 1 e 2 centrate ai due estremi del lato di lunghezza 10. Queste evidentemente non si possono intersecare e definire quindi il terzo vertice).
Sia a il lato maggiore tra i tre del triangolo. Dalla disuguaglianza triangolare discende che
![]()
Sommando ad entrambi i membri a otteniamo
![]()
che è equivalente alla
![]()
Nella funzione LLL tale controllo viene realizzato individuando il lato maggiore con la funzione Max e quindi si verifica la precedente disuguaglianza.
Per la determinazione degli angoli si utilizza una funzione di base derivata dal teorema di Carnot.
![LLL[a_, b_, c_] := Module[{α, β, γ}, &nbs ... ; ]](images/index_16.gif)
Funzione LLA
Funzione LLA
La definizione della funzione LLA è certamente più complessa delle altre e pertanto risulta conveniente suddividerla in più parti ciascuna controllata da comandi condizionali IF. Nel seguito, per ciascuna eventualità, chiariamo sia il significato geometrico che quello algebrico.
Difatti, supponiamo siano dati i due lati a e b e l'angolo α (figura 1). Nella situazione geometrica rappresentata (e l'analoga per α ottuso) appare evidente che, qualsiasi sia l'angolo γ nel vertice C, il lato a non interseca la retta orizzontale in modo da formare un triangolo. È cioè CH>a. Algebricamente ciò significa che
![]()
e conseguentemente l'angolo β non può esistere. Difatti, in base al teorema dei seni, dovrebbe essere
![]()
mentre risulta
![]()
![[Graphics:images/index_20.gif]](images/index_20.gif)
figura 1
La dichiarazione di LLA inizia pertanto affermando la non esistenza del triangolo se risulta soddisfatta la bsin(α)>a. In caso contrario può essere bsin(α)=a per cui si passa al Caso1.
![LLA[a_, b_, α_] := <br /> &nbs ... nbsp; ] ;](images/index_21.gif)
![&nbs ... nbsp; ] ;](images/index_22.gif)
Nell'ipotesi bsin(α)=a si possono presentare due eventualità, la prima con α acuto (figura 2) ammette l'esistenza di un triangolo rettangolo,
![[Graphics:images/index_23.gif]](images/index_23.gif)
figura 2
la seconda con α ottuso (figura 3) e non può produrre alcun triangolo (α diverrebbe un angolo esterno al triangolo). Dal punto di vista algebrico discende che
![]()
![[Graphics:images/index_25.gif]](images/index_25.gif)
figura 3
Queste due situazioni vengono trattate in particolare dalla funzione Caso2, nella quale se è vera la α≥![]() , si conclude con l'impossibilità dell'esistenza del triangolo mentre in caso contrario il triangolo è retto in β e lo si determina facilmente.
, si conclude con l'impossibilità dell'esistenza del triangolo mentre in caso contrario il triangolo è retto in β e lo si determina facilmente.
![&nbs ... nbsp; ] ;](images/index_27.gif)
Se bsin(α) < a, la funzione Caso1 passa il controllo alla funzione Caso3.
![&nbs ... nbsp; ] ;](images/index_28.gif)
Questa, nell'ipotesi che sia b<a (figura 4)
![[Graphics:images/index_29.gif]](images/index_29.gif)
figura 4
ammette un'unica soluzione per ogni α < π. Sopra è infatti rappresentata la situazione con α acuto, sotto (fig. 5) con α ottuso.
![[Graphics:images/index_30.gif]](images/index_30.gif)
figura 5
La trattazione algebrica di queste situazioni si può condurre imponendo la condizione che la somma α + β < π. Difatti, dalla
![]()
si possono determinare due valori supplementari di β, diciamo β (acuto) e β1 = π - β (ottuso). Imponendo che
![]()
Ora se π - α≥ ![]() ossia α≤
ossia α≤![]() la disuguaglianza è sempre soddisfatta mentre se α>
la disuguaglianza è sempre soddisfatta mentre se α>![]() , considerando il seno di entrambi i membri, si ricava
, considerando il seno di entrambi i membri, si ricava
![]()
In entrambe le situazioni quindi si giunge ad un solo triangolo.
Scegliendo invece la soluzione β1=π-β, si constata subito che la disuguaglianza α+β1<π è soddisfatta solo per b>a. Difatti
![]()
Supposto α<![]() (in caso contrario non vi possono essere soluzioni) e considerando il seno dei due membri si ottiene
(in caso contrario non vi possono essere soluzioni) e considerando il seno dei due membri si ottiene
![]()
Non si ottengono pertanto ulteriori soluzioni considerando la seconda soluzione β1.
Le rimanenti due possibilità (b = a e b > a) vengono demandate alla funzione Caso4.
![&nbs ... nbsp; ] ;](images/index_40.gif)
Dal punto di vista geometrico l'unica possibilità viene rappresentata dalla figura 6
![[Graphics:images/index_41.gif]](images/index_41.gif)
figura 6
che mostra come il triangolo debba essere isoscele. Algebricamente dalla
![]()
La prima eventualità fornisce il triangolo isoscele mentre la seconda non soddisfa evidentemente alla α+β1<π. Le possibilità fin qui discusse rientrano nell'If che viene percorso quando è vera l'uguaglianza b=a. Ovviamente se α≥![]() il triangolo non esiste mentre, come già detto, è isoscele in caso contrario.
il triangolo non esiste mentre, come già detto, è isoscele in caso contrario.
Se b>a il controllo passa infine alla funzione Caso5.
![]()
Se α≥![]() la rappresentazione geometrica (figura 7) suggerisce l'assenza di soluzioni.
la rappresentazione geometrica (figura 7) suggerisce l'assenza di soluzioni.
![[Graphics:images/index_46.gif]](images/index_46.gif)
figura 7
Questa impossibilità si dimostra algebricamente ponendo ancora α+β<π. Poiche' α≥![]() , β non potrà che essere acuto per cui
, β non potrà che essere acuto per cui
![]()
Considerando il seno di entrambi i membri (sono entrambi minori di ![]() )
)
![]()
Tutto ciò viene tenuto presente dalla prima eventualità entro il primo If.
Nell'ultima eventualità rimasta è α<![]() . In tal caso la funzione Triangoli (nella quale, per comodità di lettura si sono definite 4 variabili locali) fornisce le due soluzioni esistenti:
. In tal caso la funzione Triangoli (nella quale, per comodità di lettura si sono definite 4 variabili locali) fornisce le due soluzioni esistenti:
![&nbs ... nbsp; ] ;](images/index_52.gif)
queste vengono suggerite dalla rappresentazione geometrica di figura 8.
![[Graphics:images/index_046.gif]](images/index_046.gif)
figura 8
Difatti la figura mostra che in corrispondenza del medesimo α si possono individuare due angoli opposti al lato di lunghezza b, uno acuto e l'altro ottuso. Entrambe cioè le soluzioni della
![]()
soddisfano alla diseguaglianza α+β<π (α+β1<π). Nel primo caso
![]()
![]()
Nel secondo caso è
![]()
Considerando il seno di entrambi i membri
![]()
Un'ultima osservazione: nella chiamata alla funzione ![]() si deve porre attenzione al fatto che il primo argomento rappresenta la lunghezza del lato opposto all'angolo inserito come terzo argomento.
si deve porre attenzione al fatto che il primo argomento rappresenta la lunghezza del lato opposto all'angolo inserito come terzo argomento.
Esempi
Portiamo alcuni esempi delle funzioni definite sopra.
Funzione LAL
![]()
![( 8 - 2 Sqrt[3] ... π ------ 6 Sqrt[5 - 2 Sqrt[3]]](images/index_60.gif)
Funzione AAL
![]()
![( π ) ------ 3 1 ... 5 π 1 + Sqrt[3] -------- ----------- 12 Sqrt[6]](images/index_62.gif)
Verifichiamo come non si ottenga nessun triangolo se la somma degli angoli è maggiore di π.
![]()
![]()
Va tenuto presente che non è indifferente scambiare gli angoli dati in questa funzione. Difatti si deve considerare che il terzo dato cioè il lato, va inteso come il lato opposto al primo angolo immesso (si veda la definizione): in caso contrario si ottiene un triangolo diverso.
![]()
![( π ) ------ 4 ... 5 π 1 -------- - (1 + Sqrt[3]) 12 2](images/index_66.gif)
Funzione ALA
![]()
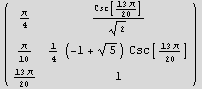
Funzione LLL
![]()
![( π ) ------ 6 Sqrt[6] ... 12 3 + Sqrt[3] π ------ 4 2 Sqrt[3]](images/index_70.gif)
Come per la funzione AAL, se non viene rispettata la disuguaglianza triangolare non si ottiene alcun triangolo valido.
![]()
![]()
Funzione LLA
![]()

![]()
![( π ) ------ 6 1 ... ------ 6 1 2 π -------- 3 Sqrt[3]](images/index_76.gif)
![]()
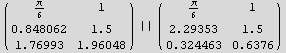
![]()
![( π ) || ( π ) ... ------ 2 20 Sqrt[6] 6 10 Sqrt[6]](images/index_80.gif)
Come in AAL pure in LLA è importante l'ordine di inserimento dei due lati noti. L'angolo che si inserisce nella funzione LLA è quello opposto al lato inserito per primo nella funzione. Difatti con i dati seguenti otteniamo
![]()
![( 5 π ) -------- ... 6 Sqrt[2] π ------ 3 6 Sqrt[3]](images/index_82.gif)
mentre nel caso che sia
![]()
![]()
il triangolo addirittura non esiste.
Ritorna all'inizio pagina