01FormuleGoniometriche.nb

Formule goniometriche

Deduzione delle principali identità goniometriche

Lorenzo Roi

Premessa

Questo notebook presenta le deduzioni delle principali identità goniometriche a partire dalle definizioni delle funzioni , e introdotte invece nel notebook IntroduzioneFunzGonio e sostanzialmente indipendente da questo. A partire dall'identità fondamentale della Goniometria si trattano quindi i valori delle funzioni goniometriche di angoli associati per passare poi, con il supporto di un'animazione grafica, alle formule di addizione e sottrazione e relative conseguenze. Si ottengono infine le formule di Werner e prostaferesi.

Nota didattica

Poiché Mathematica procede in automatico ad elaborare argomenti numerici o simbolici di funzioni nonché valori delle stesse fornendo di norma i risultati del calcolo senza presentare i passaggi intermedi, tale caratteristica ovviamente utile in numerose occasioni diventa al contrario un condizionamento tutte le volte che si intende sviluppare un graduale processo deduttivo nel quale l'uso di manipolazioni algebriche di un'espressione conduca alla dimostrazione di un asserto. Se ad esempio si considera il semplice input seguente

Mathematica semplifica automaticamente il primo membro riducendolo a per cui, essendo uguale al secondo, fornisce in output l'esito del confronto con True. In ambiti opportuni può invece essere conveniente mantenere l'input, o parti di esso, inalterato nell'output. In sostanza, Mathematica sembra inadatto in quelle situazioni, peraltro attività comune per l'insegnante, dove all'importanza o all'utilità dei risultati si affianca pure l'obiettivo di una loro documentata deduzione.

Nota tecnica

Questo notebook rappresenta sostanzialmente una sperimentazione personale attorno ad alcune funzioni raramente usate in Mathematica allo scopo di poter, in qualche modo, aggirare l'ostacolo accennato nella nota precedente. Pur esistendo in Internet alcuni interventi su queste problematiche (non molti per la verità) sotto forma di notebook o package e certamente più ampi e approfonditi di questo tentativo, ho preferito non utilizzarli per provare soluzioni più limitate e controllabili anche se meno generali. Il processo di calcolo di Mathematica è pertanto stato aggirato creando gradualmente una base di regole per le "nuove" funzioni sen[], cos[] e tan[] evitando di utilizzare le funzioni predefinite Sin[], Cos[] e Tan[]. Quando opportuno, si è "congelato" momentaneamente l'automatismo di calcolo di Mathematica con la funzione HoldForm per poi riattivarlo con una funzione (rilascia) creata ad hoc. In ogni caso si è cercato di sviluppare un insieme di funzioni minimale allo scopo.
I comandi che vanno eseguiti prima di procedere alle varie deduzioni sono quelli contenuti nella sezione Funzioni di base e quelli inseriti all'inizio di ogni sezione e compresi in Identità dimostrate. Altre brevi informazioni sulle funzioni implementate si trovano sotto forma di commenti nella sezione che segue.

Funzioni di base

Le seguenti funzioni vanno elaborate per poterne disporre in seguito nel notebook.

$RowBox[{ , RowBox[{Off[General :: spell, General :: spell1] ;,  ... p; Power[sen[α_], 2]] Power[tan[α], 2]} ;}]}]$

Identità fondamentale

Istruzioni grafiche

α = 50Degree ; pP = {Cos[α], Sin[α]} ; pQ = {Cos[α], 0} ; origine = {0, 0} ... 0, α}]}}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α], ;}]

Grafico e definizioni relative all'angolo α

[Graphics:HTMLFiles/index01_9.gif]

Dimostrazione dell'identità fondamentale

Riportiamo le definizioni di carattere geometrico delle principali funzioni goniometriche discusse in un precedente notebook e, assieme, forniamo le relazioni che le legano tra di loro al medesimo angolo . I segmenti e vanno considerati come segmenti orientati (o componenti del vettore ). è invece la misura (positiva) del raggio della circonferenza associata al sistema cartesiano di figura (o anche il modulo di ). È questo l'insieme di "regole" da cui iniziamo.

L'applicazione del teorema di Pitagora al triangolo permette di scrivere

per cui sostituendo le espressioni di e dedotte dalle definizioni di seno e coseno si ha

Eliminando ora il termine comune ai due membri si ottiene

relazione che costituisce l'identità fondamentale della Goniometria.

(* la funzione, qui usata per la prima volta, aggiunge all ' insieme di regole iniziali quella ... rensive di tutti i nomi si veda la sezione riassuntiva finale *)idFondamentale = toRule[%]

Funzioni goniometriche in termini di una di esse

Identita dimostrate

Nota la funzione

Per determinare il coseno e la tangente in termini del seno dello stesso angolo facciamo uso dell'identità appena dimostrata esplicitando dapprima il coseno ossia sottraendo ad entrambi i membri

L'estrazione della radice quadrata fornisce

ma dato che risulta

La funzione tangente invece si ottiene partendo dalla

e considerandola in valore assoluto

Sostituendo il risultato precedente giungiamo alla relazione cercata

Nota la funzione

In modo del tutto analogo si procede se si intende esprimere il seno e tangente in termini del coseno: riportiamo senza commento la procedura.

Nota la funzione

Ritenendo conosciuto il valore di iniziamo dalla evidente identità

e riscriviamo il denominatore () del secondo membro sfruttando l'identità fondamentale

Dividiamo ora il numeratore e denominatore del secondo membro per supponendo quindi che

sen[α]^2sen[α]^2/cos[α]^2/(cos[α]^2 + sen[α]^2)/cos[α]^2

Applicando la proprietà distributiva e sapendo che otteniamo

da cui l'estrazione della radice quadrata in entrambi i membri fornisce

per cui risulta

Con la stessa successione di passaggi si ottiene il valore assoluto del coseno in termini della tangente: sinteticamente

cos[α]^2cos[α]^2/cos[α]^2/(cos[α]^2 + sen[α]^2)/cos[α]^2

Identità dimostrate

In definitiva abbiamo ottenuto le seguenti identità in termini dell'angolo

{idFondamentale, cosNotosen, tanNotosen, senNotocos, tanNotocos, senNototan, cosNototan} = {co ... otosen, tanNotosen, senNotocos, tanNotocos, senNototan, cosNototan}}]//TableForm//TraditionalForm

idFondamentale
cosNotosen
tanNotosen
senNotocos
tanNotocos
senNototan
cosNototan

Nel seguito riprenderemo, di queste, solo l'identità fondamentale in quanto solo questa si dimostrerà necessaria.

Angoli associati e relative identità

Angoli complementari

Istruzioni grafiche

α = 20Degree ; β = (π/2 - α) ; pP = {Cos[α], Sin[α]} ; pQ = {Cos ... ;}]}}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;}]

Grafico

[Graphics:HTMLFiles/index01_116.gif]

Identità dimostrate

${idFondamentale} = {cos[α_]^2 + sen[α_]^21} ;$

Seno di un angolo complementare

Sia l'ampiezza di un angolo orientato. Questo individua nella circonferenza con centro nell'origine di un sistema cartesiano il triangolo . In fig. 2 , per comodità, appare un angolo compreso nel I quadrante (in rosso) ma le relazioni che dedurremo si dimostrano valide qualsiasi sia il suo valore. L'angolo complementare, di ampiezza che si associa ad definisce a sua volta il triangolo : siamo interessati ad esprimere le funzioni goniometriche di quest'ultimo in termini di quelle dell'angolo . Dalla definizione discende quindi che

ma la congruenza tra i triangoli comporta che si abbia, anche in segno, e . Pertanto sostituendo queste uguaglianze nella precedente

Ma per la definizione delle funzioni goniometriche relative all'angolo , in particolare quella del coseno, risulta che

Identità dimostrate

${idFondamentale, senCompl} = {cos[α_]^2 + sen[α_]^21, sen[π/2 - α_] cos[α]} ;$

Coseno di un angolo complementare

Procediamo nello stesso modo per determinare in termini di funzioni dell'angolo .

Osservata la validità di (fig.2) discende

e utilizzando la definzione di

Identità dimostrate

${idFondamentale, senCompl, cosCompl} = {cos[α_]^2 + sen[α_]^21, sen[π/2 - α_] cos[α], cos[π/2 - α_] sen[α]} ;$

Tangente di un angolo complementare

Infine, la definizione di tangente per l'angolo complementare comporta l'uguaglianza

ma la congruenza dei triangoli già esposta assicura che e (fig. 2) per cui

che è equivalente alla

Per la definizione di tangente risulta anche

da cui, dividendo per

che si può riscrivere nei due modi seguenti

In alternativa

tan[π/2 - α] sen[π/2 - α]/cos[π/2 - α]

per cui sfruttando le identità già dimostrate per seno e coseno, riesce

Abbiamo pertanto dimostrato le identità:

Angoli complementari sen(π/2 - α) = cos(α) cos(π/2 - α) = sen(α) tan(π/2 - α) = cot(α) = 1/tan(α)

Angoli che differiscono per un angolo retto

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl} = {cos[α_]^2 + sen[α_]^21, se ... 945;], cos[π/2 - α_] sen[α], tan[π/2 - α_] cot[α]} ;$

Istruzioni grafiche

α = 20Degree ; β = π/2 + α ; pP = {Cos[α], Sin[α]} ; pQ = {Cos[& ... }}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;, ;}]

Grafico

[Graphics:HTMLFiles/index01_179.gif]

Seno di un angolo che differisce di

Angoli che differiscono per un angolo retto danno origine alla configurazione geometrica di fig. 3. Ancora è soddisfatta la congruenza di tipo geometrico mentre, osservando i versi delle componenti, risulta e . Ne segue

che si riscrive

e, in base alla definizione, risulta

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2} = {cos[α_]^2 + sen[α_]^2& ... 945;], tan[π/2 - α_] cot[α], sen[π/2 + α_] cos[α]} ;$

Coseno di un angolo che differisce di

Dalla definizione

ma per quanto osservato sopra nel caso del seno diviene

per cui

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2} = {cos[α_]^2 + sen ... 5;], sen[π/2 + α_] cos[α], cos[π/2 + α_]  -sen[α]} ;$

Tangente di un angolo che differisce di

Con le medesime osservazioni e iniziando dalla definizione

risulta che l'espressione precedente si modifica in

da cui, moltiplicando per il reciproco del secondo membro

si ottiene un'espressione dove appare la definizione di

Dividendo per tale funzione si ha

che si può riscrivere anche come

Riassumiamo in riquadro quanto ottenuto

Angoli che differiscono per un angolo retto sen(π/2 + α) = cos(α) cos(π/2 + α) = -sen(α) tan(π/2 + α) = -cot(α) = -1/tan(α)

Angoli supplementari

Istruzioni grafiche

α = 30Degree ; β = π - α ; pP = {Cos[α], Sin[α]} ; pQ = {Cos[ ... ;}]}}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;}]

Grafico

[Graphics:HTMLFiles/index01_221.gif]

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2} = {cos[^ ... ;/2 + α_]  -sen[α], tan[π/2 + α_]  -cos[α]/sen[α]} ;$

Seno di un angolo supplementare

Ancora una volta l'espressione delle funzioni goniometriche di un angolo associato ad , in tal caso l'angolo supplementare, si basa sull'osservazione della congruenza dei triangoli individuati dai lati terminali dei due angoli, nel caso in esame, e (fig. 4). Valgono pertanto le relazioni tra componenti e e di conseguenza discende

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl} = ... #960;/2 + α_]  -cos[α]/sen[α], sen[π - α_] sen[α]} ;$

Coseno di un angolo supplementare

Nello stesso modo

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... α], sen[π - α_] sen[α], cos[π - α_]  -cos[α]} ;$

Tangente di un angolo supplementare

Infine, la definizione di tangente implica

e le osservazioni fatte inizialmente permettono di riscriverla come

da cui

Abbiamo dimostrato quindi le ulteriori tre relazioni

Angoli supplementari sen(π - α) = sen(α) cos(π - α) = -cos(α) tan(π - α) = -tan(α)

Angoli che differiscono di π

Istruzione grafiche

α = 30Degree ; β = π + α ; pP = {Cos[α], Sin[α]} ; pQ = {Cos[ ... ;}]}}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;}]

Grafico

[Graphics:HTMLFiles/index01_256.gif]

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 945;], cos[π - α_]  -cos[α], tan[π - α_]  -tan[α]} ;$

Seno di un angolo che differisce di π (angolo explementare)

Con riferimento alla fig. 5 osserviamo al solito modo che così come . Poiché per definizione risulta

le precedenti danno luogo alla

e quindi, riprese le definizioni per l'angolo , segue

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 945;], tan[π - α_]  -tan[α], sen[π + α_]  -sen[α]} ;$

Coseno di un angolo che differisce di π (angolo explementare)

La definizione di coseno implica per l'angolo explementare (fig. 5)

ma le relazioni tra componenti già discusse permettono di scrivere

da cui

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 945;], sen[π + α_]  -sen[α], cos[π + α_]  -cos[α]} ;$

Tangente di un angolo che differisce di π (angolo explementare)

Infine sfruttando ancora la definizione di tangente

e le relazioni tra componenti

risulta

Questa identità conferma e dimostra la periodicità della funzione tangente: il suo periodo � pari a .

In definitiva abbiamo che le funzioni goniometriche di angoli esplementari sono collegate a quelle dell'angolo originario dalle seguenti identità

Angoli che differiscono di π sen(π + α) = -sen(α) cos(π + α) = -cos(α) tan(π + α) = tan(α)

Angoli opposti

Grafico

α = 30Degree ; β = -α ; pP = {Cos[α], Sin[α]} ; pQ = {Cos[α], 0} ... ;}]}}, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;}]

Grafico

[Graphics:HTMLFiles/index01_290.gif]

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... α], cos[π + α_]  -cos[α], tan[π + α_] tan[α]} ;$

Seno di un angolo opposto

Dalla congruenza più volte notata discende ora e (fig. 6). Ne deriva che

Questo risultato, valido per stabilisce che la funzione seno è una funzione dispari: il suo grafico risulta pertanto simmetrico rispetto all'origine di un sistema cartesiano che abbia in ascissa la variabile angolare e in ordinata il valore .

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 1; -cos[α], tan[π + α_] tan[α], sen[-α_]  -sen[α]} ;$

Coseno di un angolo opposto

Analogamente a quanto finora visto e in base alla configurazione di fig. 6

Anche questa identità, valida per codifica una proprietà importante della funzione coseno: questa è una funzione pari con grafico simmetrico rispetto all'asse delle ordinate del sistema cartesiano associato all'equazione .

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... ;_] tan[α], sen[-α_]  -sen[α], cos[-α_] cos[α]} ;$

Tangente di un angolo opposto

Per la definizione di tangente e in base a quanto osservato precedentemente

Come già visto per la funzione seno, poiché l'identità precedente vale per stabilisce che pure la funzione tangente è una funzione dispari con grafico quindi simmetrico rispetto all'origine di un sistema cartesiano con in ascissa la variabile angolare e in ordinata il valore di .

Abbiamo ottenuto quindi

Angoli opposti sen(-α) = -sen(α) cos(-α) = cos(α) tan(-α) = -tan(α)

Introduzione grafica e prima identità

Analisi grafica

Affrontiamo in questa sezione la dimostrazione dell'identità che lega il coseno di una differenza di angoli alle funzioni goniometriche degli angoli stessi. In base a questa relazione sarà possibile dedurre una (lunga) serie di identità che specificano di volta in volta nuove proprietà delle funzioni goniometriche.
Definiamo nella circonferenza goniometrica i due angoli e , il primo indicato in giallo nella figura sottostante e tale da ricoprire un intero settore circolare di e il secondo in verde.

I lati non coincidenti con il semiasse positivo delle di questi angoli intersecano la circonferenza nei due punti, e .

Istruzioni grafiche

RowBox[{RowBox[{Show, [, RowBox[{Graphics[{{colGiallo, Disk[{0, 0}, 1, {0, α}]}, {colVerd ... estileTesto]}], }}], ]}], ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;}]

Grafico

[Graphics:HTMLFiles/index01_339.gif]

Dal punto di vista geometrico, la differenza appare come l'angolo evidenziato in color rosso. Poiché le convenzioni sugli angoli in goniometria impongono di trattare questi con un lato coincidente con il semiasse positivo delle ascisse, eseguiamo una rotazione attorno all'origine pari all'angolo in modo da riportare quest'angolo nell'ambito convenzionale corretto.

Istruzioni grafiche

nPassi = 50 ; suddivisioneAngolo = Range[0, β, β/nPassi] ; estremiAngoli = {β - ... }, ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], &}], /@, estremiAngoli}], ;}]

Animazione

Appare evidente come in tale rotazione il punto , alla fine, vada a coincidere con il punto di fig. 8 mentre il punto a sua volta ha per immagine finale il punto .

In particolare, essendo le rotazioni delle isometrie, la lunghezza della corda rimane invariata cosicché possiamo porre in relazione la lunghezza del segmento originario con quella della sua immagine : queste lunghezze sono uguali per cui vale oppure, elevando al quadrato

Istruzioni grafiche

RowBox[{RowBox[{Show, [, RowBox[{RowBox[{Graphics, [, RowBox[{{, RowBox[{Circle[{0, 0}, 1], ,, ... }}]}], ,, AspectRatioAutomatic, ,, AxesTrue}], ]}], ;, Clear[α, β], ;}]

Grafico

[Graphics:HTMLFiles/index01_355.gif]

Formula di sottrazione per il coseno

Identità dimostrate

$Clear[α, β, "p*"] ; {idFondamentale, senCompl, cosCompl, tanCompl, senDiff ...  -sen[α], cos[-α_] cos[α], tan[-α_]  -tan[α]} ;$

Dimostrazione

Poiché i punti , , e sono descritti dalle coppie ordinate

pP = {cos[α], sen[α]} ; pQ = {cos[β], sen[β]} ; pA = {1, 0} ; pD = {cos[α - β], sen[α - β]} ;

ne segue che i quadrati dei segmenti dPQquadro e dDAquadro in termini degli angoli e risultano

${{"PQquadrato =", PQquadrato = Plus @@ (pP - pQ)^2}, {"DAquadrato =", DAquadrato = Plus @@ (pD - pA)^2}}//TableForm$

PQquadrato =
DAquadrato =

Posti, per quanto visto, uguali ne discende l'equazione

Possiamo ora eseguire i quadrati coinvolti nei due membri

e quindi utilizzando l'identità goniometrica fondamentale , ridurre l'equazione alla forma equivalente più semplice

Sottraendo ad entrambi i membri

e, dopo aver diviso per , scambiamo i due membri e semplifichiamo

In definitiva siamo giunti a dimostrare la validità dell'espressione

Il coseno di una differenza è pertanto, ben diverso dall'aspettativa ingenua che lo "vorrebbe" pari alla differenza dei coseni! In termini più formali questa identità (e le analoghe seguenti) dimostrano che le funzioni goniometriche non sono delle funzioni lineari dei propri argomenti.

Formule di addizione e sottrazione

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... -tan[α], cos[α_ - β_] cos[α] cos[β] + sen[α] sen[β]} ;$

Formula di addizione per il coseno

La precedente identità collega il coseno della differenza di due angoli e con le funzioni goniometriche di questi e costituisce la formula di sottrazione per il coseno. Questo risultato si può facilmente estendere e in questa sezione otterremo, per prima, la corrispondente formula di addizione e successivamente le formule di addizione e sottrazione per seno e tangente. A tal fine sostituiamo nell'identità appena dimostrata

all'angolo l'angolo

Tenendo presente quanto già dimostrato ossia che il seno è una funzione dispari valendo mentre il coseno è pari dato che , l'espressione precedente diviene

Il coseno della somma in termini delle funzioni di e risulta quindi

Formule di addizione e sottrazione per il seno

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... ] sen[β], cos[α_ + β_] cos[α] cos[β] - sen[α] sen[β]} ;$

Seno della differenza

Sfruttiamo l'identità per dedurre la formula di sottrazione per la funzione seno.

e, in base alla proprietà associativa, riscriviamo il secondo membro sostituendo a

Possiamo ora applicare la formula di addizione per il coseno appena ottenuta

e ritornando ad esprimere in termini di

Per l'identità già ricordata e per quella analoga riguardante il seno di angoli complementari , la precedente fornisce

che è quanto si voleva ottenere.

Identità dimostrate

$senDiffEq = sen[α - β] cos[β] sen[α] - cos[α] sen[β] ; { ... sen[β], sen[α_ - β_] cos[β] sen[α] - cos[α] sen[β]} ;$

Seno della somma

Nello stesso modo seguito per il coseno, sostituiamo a l'angolo

Per le proprietà di simmetria del seno e del coseno, , otteniamo

Riassumiamo in un'unica espressione le due identità dimostrate

intendendo che i segni vanno considerati nell'ordine indicato ossia il segno superiore a primo membro va associato al segno superiore a secondo e così per quello inferiore.

Formule di addizione e sottrazione per la tangente

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... ] sen[β], sen[α_ + β_] cos[β] sen[α] + cos[α] sen[β]} ;$

Tangente della somma

Sfruttiamo le identità appena trovate per dimostrare quelle coinvolgenti la tangente di una somma o di una differenza. Poiché la tangente di un angolo si può esprimere come il rapporto tra il seno e il coseno, abbiamo

Sviluppiamo il numeratore e denominatore della precedente utilizzando le formule di addizione per il seno e coseno

Supponendo cioè , dividiamo numeratore e denominatore del secondo membro per tale termine

tan[α + β]  (cos[β] sen[α] + cos[α] sen[β])/(cos[α] cos[β])/(cos[α] cos[β] - sen[α] sen[β])/(cos[α] cos[β])

e quindi semplificando e tenendo conto della definizione di tangente in termini del seno e coseno, gli elementi coinvolti a secondo membro divengono rispettivamente

tan[α + β]  (sen[α]/cos[α] + sen[β]/cos[β])/(1 - (sen[α] sen[β])/(cos[α] cos[β]))

che è la formula cercata.

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 46;], tan[α_ + β_]  (tan[α] + tan[β])/(1 - tan[α] tan[β])} ;$

Tangente della differenza

Per ottenere la formula corrispondente e relativa alla differenza degli angoli, procediamo alla sostituzione

Ricordando che la tangente è una funzione dispari che soddisfa quindi alla identità giungiamo infine alla

In definitiva le formule di addizione e sottrazione per la tangente sono

Formule di duplicazione

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 6;]), tan[α_ - β_]  (tan[α] - tan[β])/(1 + tan[α] tan[β])} ;$

Formule di duplicazione per seno coseno e tangente

Dall'insieme delle formule discusse finora possiamo derivare facilmente un altro gruppo di importanti identità goniometriche. Iniziamo da quelle di duplicazione, formule che collegano le funzioni goniometriche dell'angolo con quelle dell'angolo .
Partendo dalla

basta porre per ottenere quanto si voleva

Analogamente per il coseno si ottiene immediatamente

Tenendo conto dell'identità goniometrica fondamentale quest'ultima si può riscrivere anche in termini alternativi appena si sostituisca

oppure ancora, in base alla , si ottiene una terza forma

Infine la formula di addizione per la tangente

fornisce con la sostituzione l'espressione cercata

Le formule di duplicazione sono pertanto

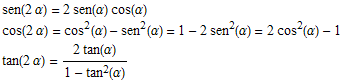
sen(2α) = 2sen(α) cos(α)  cos(2α) = cos^2(α) - sen^2(α) ... - 2sen^2(α) = 2cos^2(α) - 1  tan(2α) = (2tan(α))/(1 - tan^2(α))

Formule di bisezione

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 5;_]  -1 + 2 cos[α]^2, tan[2 α_]  (2 tan[α])/(1 - tan[α]^2)} ;$

Formule di bisezione per seno, coseno, tangente

In modo inverso rispetto alle formule di duplicazione, quelle di bisezione esprimono le funzioni goniometriche di un angolo in termini dell'angolo doppio. Iniziamo sfruttando una delle tre forme della formula di duplicazione per il

ed esplicitiamo il in funzione del

L'estrazione della radice quadrata comporta

e quindi ricordando che il primo membro rappresenta un valore assoluto, l'espressione diventa

Sostituendo ad l'angolo otteniamo quanto richiesto

Si tenga presente che per utilizzare proficuamente formule di questo tipo, contenenti il valore assoluto di una funzione goniometrica, sarà necessario conoscere il quadrante dell'angolo così da riconoscere il segno della funzione ad argomento e "aprire" il valore assoluto.

Abbiamo in sostanza dimostrato

Partendo invece dalla forma

esplicitiamo il

e quindi l'estrazione della radice quadrata conduce alla

ossia

Eseguiamo infine la sostituzione per ottenere la scrittura canonica per tale identità

Volendo giungere anche alla formula di bisezione per la tangente è sufficiente eseguire il rapporto, membro a membro, delle due identità appena trovate: ovviamente quanto si deduce vale nell'ipotesi che il denominatore sia diverso dallo zero (). Difatti

Abs[sen[α/2]]/Abs[cos[α/2]]  (1 - cos[α])^(1/2)/(1 + cos[α])^(1/2)

Possiamo quindi porre

Le tre identità ottenute sono in conclusione

Formule parametriche razionali

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... ;])^(1/2)/2^(1/2), Abs[Tan[α_/2]]  (1 - cos[α])^(1/2)/(1 + cos[α])^(1/2)} ;$

Formule parametriche razionali di seno, coseno e tangente

Le formule che dimostreremo in questa sezione si mostrano utili in diverse occasioni, in particolare quando non si dispone di sufficienti informazioni sul quadrante di appartenenza dell'angolo . Difatti nelle seguenti relazioni non compaiono termini entro valori assoluti per i quali è necessario disporre di tale informazione.
Partiamo dalla formula di duplicazione del seno

e scriviamo il denominatore del secondo membro (che vale evidentemente 1) come .

$MapAt[# 1/(sen[α]^2 + cos[α]^2) &, %, {2}]$

Dividiamo ora il numeratore e il denominatore per supponendo quindi che

sen[2 α]  (2 cos[α] sen[α])/cos[α]^2/(cos[α]^2 + sen[α]^2)/cos[α]^2

Ricordando che il secondo membro si riscrive

Infine per riportare l'identità appena trovata alla forma canonica eseguiamo la sostituzione

sen[α]  (2 tan[α/2])/(1 + tan[α/2]^2)

sen[α]  (2 tan[α/2])/(1 + tan[α/2]^2)

Procedendo allo stesso modo possiamo giungere all'identità collegata al coseno: difatti, riscritta

come

$MapAt[# 1/(sen[α]^2 + cos[α]^2) &, %, {2}]$

dividiamo ancora il numeratore e il denominatore per supponendo quindi che

cos[2 α]  (cos[α]^2 - sen[α]^2)/cos[α]^2/(cos[α]^2 + sen[α]^2)/cos[α]^2

Per la proprietà distributiva e la definizione della tangente, questa diviene

L'applicazione della sostituzione implica

cos[α]  (1 - tan[α/2]^2)/(1 + tan[α/2]^2)

cos[α]  (1 - tan[α/2]^2)/(1 + tan[α/2]^2)

La terza ed ultima formula di bisezione si ottiene immediatamente con la sostituzione a partire da quella di duplicazione per la tangente

Difatti si ha

tan[α]  (2 tan[α/2])/(1 - tan[α/2]^2)

tan[α]  (2 tan[α/2])/(1 - tan[α/2]^2)

In conclusione, le formule di bisezione ottenute sono

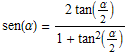sen(α) = (2tan(α/2))/(1 + tan^2(α/2))     con

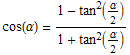cos(α) = (1 - tan^2(α/2))/(1 + tan^2(α/2))     con

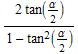tan(α)= (2tan(α/2))/(1 - tan^2(α/2))     con

Formule di Werner e prostaferesi

Identità dimostrate

${idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... 945;/2]^2)/(1 + tan[α/2]^2), tan[α_]  (2 tan[α/2])/(1 - tan[α/2]^2)} ;$

Formule di Werner

Riportate di seguito le formule di addizione e sottrazione per il seno e coseno, deduciamo da queste delle ulteriori identità con le quali potremo collegare prodotti di funzioni goniometriche con somme.

(1) senAdd	sen[α + β] == cos[β] sen[α] + cos[α] sen[β]
(2) senDiff	sen[α - β] == cos[β] sen[α] - cos[α] sen[β]
(3) cosAdd	cos[α + β] == cos[α] cos[β] - sen[α] sen[β]
(4) cosDiff	cos[α - β] == cos[α] cos[β] + sen[α] sen[β]

Sommando quindi in colonna le prime due, otteniamo

che evidentemente associa il prodotto del seno e coseno con una somma. Dividendo per 2 e scrivendo il secondo membro come primo abbiamo

espressione che costituisce la prima formula di Werner. Se, al contrario, eseguiamo la differenza delle prime due identità e procediamo allo stesso modo otteniamo

che sostanzialmente mostra il medesimo risultato a parte lo scambio dell'angolo con . Eseguendo invece la somma della terza e quarta identità

giungiamo, dopo aver scambiato i membri e diviso per

alla seconda formula di Werner: questa collega il prodotto di due coseni con una somma. Infine sottraendo la quarta dalla terza

e semplificata dividendola per e quindi scambiati i membri, ricaviamo la terza formula di Werner che riporta un prodotto di seni in una somma.

Formule di prostaferesi

Infine, le quattro formule di prostaferesi si deducono dalle espressioni intermedie servite per giungere alle relazioni di Werner. A tal fine si sostituiscono, in luogo degli angoli e , le nuove variabili

Esplicitati e in termini di e

e, dopo aver sommato la formula di addizione per il seno con quella della sottrazione,

è sufficiente sostituire le nuove variabili

e semplificare

È questa la prima formula di prostaferesi che, come appare evidente, riduce una somma di seni ad un prodotto. Le altre si ottengono in maniera analoga: per ottenere la seconda identità di prostaferesi, riferendoci sempre alle identità di inizio sezione va sottratta la seconda dalla prima

per cui, scambiati i membri

e sostituite le nuove variabili angolari si ottiene

Per la terza di prostaferesi, si parte invece dalla somma della terza identità iniziale con la quarta

e con il medesimo processo si trova

Per ultimo, sottraendo la quarta dalla terza

e, inserite le varibili e

la moltiplicazione per conduce al risultato cercato

In conclusione le 3 formule distinte di Werner sono

cos (α) sen (β) 1/2 [sen (α + β) - sen (α - β)] cos ( ... - β)] sen (α) sen (β) 1/2 [cos (α - β) - cos (α + β)]

e collegano dei prodotti di funzioni con delle somme, mentre le quattro di prostaferesi

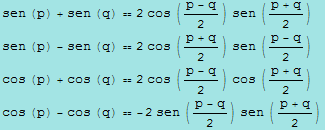
sen (p) + sen (q) 2 cos ((p - q)/2) sen ((p + q)/2) sen (p) - sen (q) 2 cos (( ... 3;2 cos ((p - q)/2) cos ((p + q)/2) cos (p) - cos (q)  -2 sen ((p - q)/2) sen ((p + q)/2)

associano a somme delle medesime funzioni, dei prodotti.

Riassunto di tutte le identità dimostrate

Identità dimostrate

{idFondamentale, cosNotosen, tanNotosen, senNotocos, tanNotocos, senNototan, cosNototan} = {co ... otosen, tanNotosen, senNotocos, tanNotocos, senNototan, cosNototan}}]//TableForm//TraditionalForm

{idFondamentale, senCompl, cosCompl, tanCompl, senDiffPi2, cosDiffPi2, tanDiffPi2, senSuppl, c ... erSenSen, proSenAddSen, proSenDiffSen, proCosAddCos, proCosDiffCos}}]//TableForm//TraditionalForm

Tabelle

Presentiamo infine due tabelle riassuntive di tutte le identità dimostrate in questo notebook con associati i rispettivi nomi simbolici usati.

Identità goniometriche dello stesso angolo

idFondamentale
cosNotosen
tanNotosen
senNotocos
tanNotocos
senNototan
cosNototan

Identità goniometriche di angoli diversi

senCompl
cosCompl
tanCompl
senDiffPi2
cosDiffPi2
tanDiffPi2
senSuppl	sen(π - α) == sen(α)
cosSuppl	cos(π - α) == -cos(α)
tanSuppl	tan(π - α) == -tan(α)
senExpl	sen(α + π) == -sen(α)
cosExpl	cos(α + π) == -cos(α)
tanExpl	tan(α + π) == tan(α)
senOpp	sen(-α) == -sen(α)
cosOpp	cos(-α) == cos(α)
tanOpp	tan(-α) == -tan(α)
cosDiff	cos(α - β) == cos(α) cos(β) + sen(α) sen(β)
cosAdd	cos(α + β) == cos(α) cos(β) - sen(α) sen(β)
senDiff	sen(α - β) == cos(β) sen(α) - cos(α) sen(β)
senAdd	sen(α + β) == cos(β) sen(α) + cos(α) sen(β)
tanAdd
tanDiff
senDupl	sen(2 α) == 2 cos(α) sen(α)
cosDupl
cosDuplSen
cosDuplCos
tanDupl
senBis
cosBis
tanBis
senRaz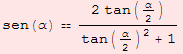
cosRaz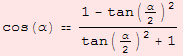
tanRaz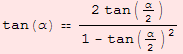
wernerCosSen
wernerCosCos
wernerSenSen
proSenAddSen
proSenDiffSen
proCosAddCos
proCosDiffCos

Ritorna all'inizio pagina