Ritorna alla pagina di presentazione
Introduzione alle derivate
Introduzione
Questo notebook di Mathematica presenta una lezione introduttiva sul significato di derivata di una funzione in un suo punto e, in particolare, introduce al suo significato geometrico. Dapprima si studia il grafico di una funzione ad ingrandimenti sempre maggiori nell'intorno di un punto del suo dominio notando come questo, nelle situazioni più semplici possa essere approssimato da una funzione lineare. Si analizza poi il comportamento delle rette secanti e del loro coefficiente angolare (o rapporto incrementale) al diminuire dell'incremento, suggerendo il significato intuitivo di retta tangente. Fornita la definizione formale di derivata si presenta infine il calcolo del limite del rapporto incrementale in alcune situazioni particolari.
Lorenzo Roi (dicembre 2011)
Codice
Grafico di una funzione in intorni di un punto
Iniziamo definendo una semplice e nota funzione goniometrica
![]()
e rappresentiamone il grafico nell'intervallo [0,2π] (sistema non isometrico).
![]()
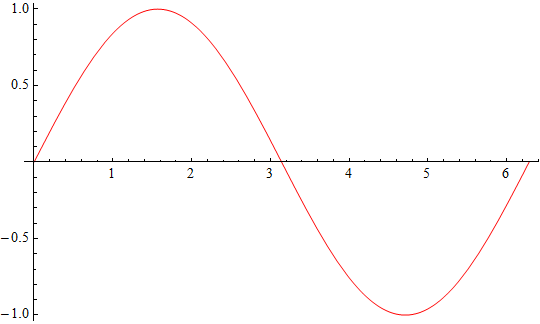
La nostra intenzione è di studiare tale grafico in intorni del punto 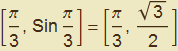 . A tal fine la funzione zoom[f,x0] permette di ottenere una serie di ingrandimenti attorno al punto
. A tal fine la funzione zoom[f,x0] permette di ottenere una serie di ingrandimenti attorno al punto ![]() del grafico della funzione f. Inizialmente l’intervallo nel quale si rappresenta l’andamento di f è centrato in
del grafico della funzione f. Inizialmente l’intervallo nel quale si rappresenta l’andamento di f è centrato in ![]() e possiede semiampiezza unitaria: muovendo il cursore verso destra si diminuisce tale semiampiezza e i nuovi estremi dell’intervallo appaiono visualizzati sopra il grafico.
e possiede semiampiezza unitaria: muovendo il cursore verso destra si diminuisce tale semiampiezza e i nuovi estremi dell’intervallo appaiono visualizzati sopra il grafico.
![]()
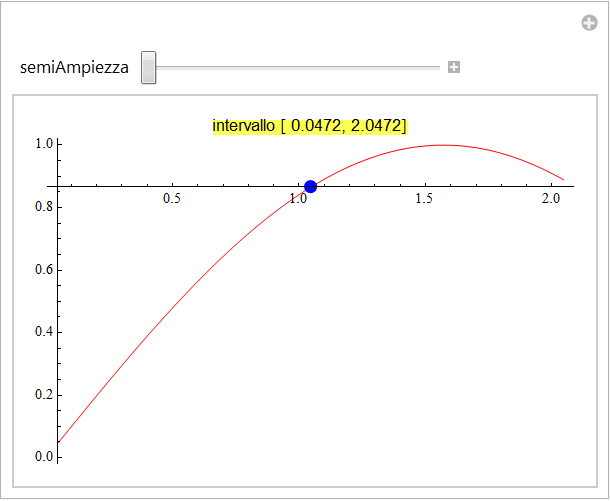
L'animazione mostra come all'aumentare dell'ingrandimento il tratto di sinusoide compreso nell’intervallo tenda ad assumere un andamento rettilineo. In una scala molto piccola quindi potremo pensare di approssimare tale arco di sinusoide con un segmento e caratterizzare quest'ultimo per mezzo del coefficiente angolare della retta che lo comprende e che, evidentemente deve passare per 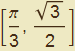 .
.
Al fine di verificare se tali osservazioni possano valere in generale, definiamo una seconda funzione e studiamone il comportamento in intorni dell'origine: la funzione g per x≠0 vale ![]() mentre è nulla se x=0.
mentre è nulla se x=0.
Lo zoom attorno all'origine fornisce i grafici seguenti
![]()
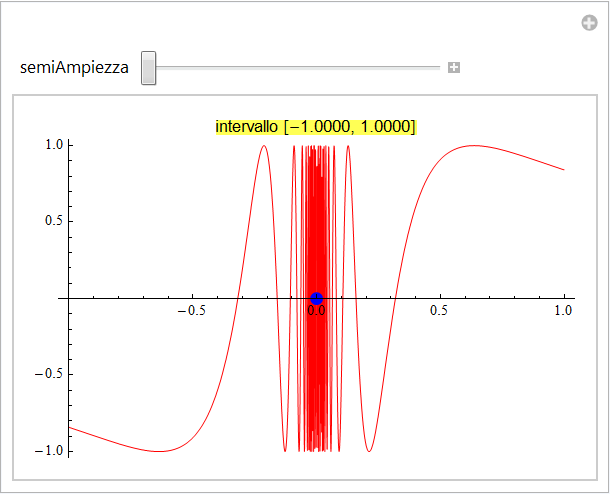
che manifestamente mostrano un comportamento del tutto diverso dal precedente (in ordinata la funzione continua ad oscillare tra 1 e -1 e all'aumentare dell'ingrandimento emergono nuove oscillazioni, sempre più fitte). Studiando la stessa funzione attorno al punto di ascissa 0.5 invece
![]()
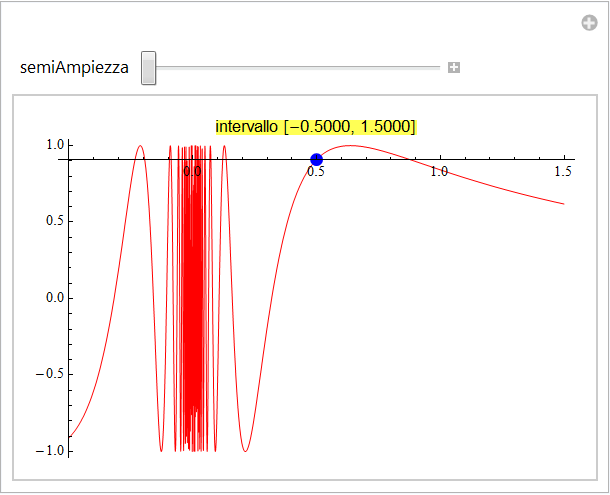
ritroviamo ancora l'andamento notato per la sinusoide. È evidente quindi che per una stessa funzione vi sono punti dove il comportamento del grafico, a scale sempre più piccole, risulta sostanzialmente differente. In particolare vi sono intorni di punti dove all'aumentare dell'ingrandimento il grafico della funzione tende ad assumere un andamento lineare mentre in altri appare sicuramente più complicato.
Nel primo caso potremo pensare di
descrivere geometricamente l’andamento di tali funzioni con una retta passante per il punto in questione e che apparirà naturale identificare con la retta tangente, mentre
dal punto di vista algebrico tale comportamento potrà essere riassunto per mezzo del coefficiente angolare di tale retta.
Nella sezione successiva cercheremo quindi di caratterizzare maggiormente le proprietà di quei punti dove l'andamento del grafico appare sostanzialmente semplice e assimilabile ad un segmento.
Definizione di rapporto incrementale e suo studio
Se il grafico di una funzione tende a divenire in intorni di un punto quello di un segmento potremo descrivere il suo andamento per mezzo di una retta passante per il punto in questione.
Siccome per ogni relazione lineare (per esempio, y=m x+q) tra due variabili x e y sussiste la costanza del rapporto tra le variazioni della variabile dipendente y con le corrispondenti variazioni della variabile indipendente e ciò, nella geometria analitica, è espresso dalla costanza del coefficiente angolare
![]()
cercheremo di individuare per questa retta il suo parametro più significativo, cioè il suo coefficiente angolare. Di conseguenza in questa sezione studiamo, inizialmente dal punto di vista grafico e, successivamente con un’analisi numerica, la variazione del coefficiente angolare di una retta passante per il punto di f ![]() , ritenuto fisso, e il punto
, ritenuto fisso, e il punto ![]() che invece verrà considerato variabile con h (quest’ultimo definito successivamente come l’incremento della variabile indipendente). Verrà quindi analizzata la convergenza o meno di tale coefficiente angolare al diminuire di h. Il coefficiente angolare di tale retta è definito, più propriamente, come il rapporto incrementale nel punto
che invece verrà considerato variabile con h (quest’ultimo definito successivamente come l’incremento della variabile indipendente). Verrà quindi analizzata la convergenza o meno di tale coefficiente angolare al diminuire di h. Il coefficiente angolare di tale retta è definito, più propriamente, come il rapporto incrementale nel punto ![]() della funzione f,
della funzione f,
in quanto è il rapporto
dell’incremento ![]() della funzione e
della funzione e
dell’incremento ![]() della variabile indipendente.
della variabile indipendente.
Tale retta è evidentemente una retta secante il grafico di f,
La figura seguente mostra graficamente le convenzioni sui nomi, la retta secante e il triangolo avente per cateti i due incrementi, Δf e Δx.
Vediamo quindi cosa succede tracciando via via le diverse rette secanti il grafico della funzione f nel punto di ascissa ![]() , quando l'incremento h tende gradualmente a valori sempre più piccoli.
, quando l'incremento h tende gradualmente a valori sempre più piccoli.
![]()
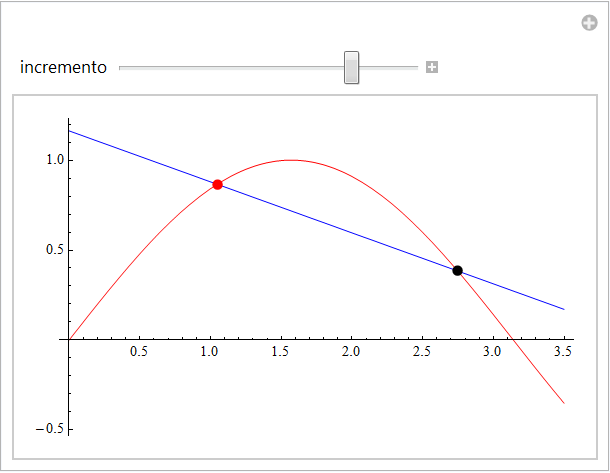
L'animazione mette in evidenza un fascio di rette proprio di centro 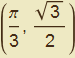 tutte secanti il grafico di f e che, al diminuire dell'incremento, suggeriscono un avvicinamento alla retta tangente. Per quanto visto precedentemente, possiamo intuire come il rapporto incrementale (cioè il loro coefficiente angolare) tenda ad assumere un valore prossimo a quello del segmento che caratterizzava il grafico della funzione a piccola scala. Per rafforzare tale osservazione mostriamo, ancora a livello grafico, il triangolo rettangolo che ha per cateti gli incrementi delle due variabili.
tutte secanti il grafico di f e che, al diminuire dell'incremento, suggeriscono un avvicinamento alla retta tangente. Per quanto visto precedentemente, possiamo intuire come il rapporto incrementale (cioè il loro coefficiente angolare) tenda ad assumere un valore prossimo a quello del segmento che caratterizzava il grafico della funzione a piccola scala. Per rafforzare tale osservazione mostriamo, ancora a livello grafico, il triangolo rettangolo che ha per cateti gli incrementi delle due variabili.
La nuova rappresentazione è ora
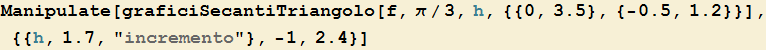
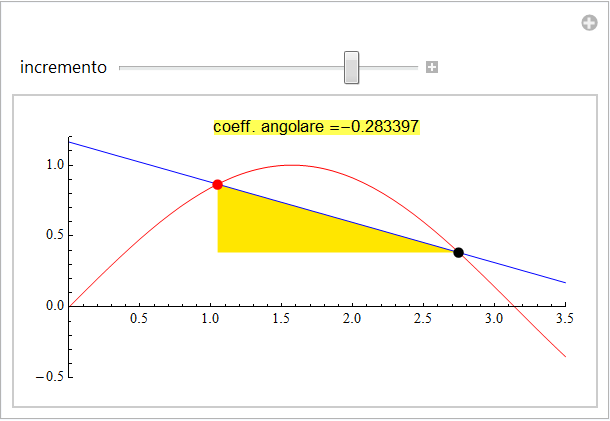
La tendenza ad assumere un valore costante (e quindi per il triangolo assumere forme simili) appare in modo più marcato osservando il comportamento a piccole scale.
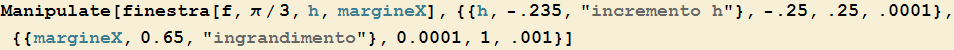
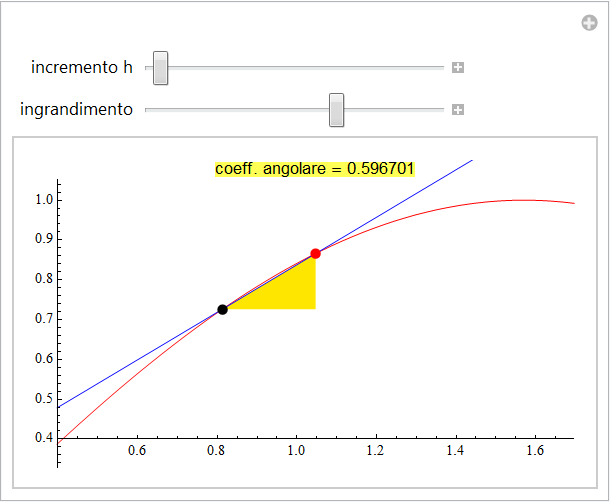
Mano a mano che il punto variabile (color nero) si avvicina a quello fisso (di colore rosso)
le rette secanti approssimano sempre meglio l’andamento della funzione in intorni del punto ![]() confondendosi con il grafico divenuto approssimativamente lineare di f. Possiamo ben dire quindi che tali rette si avvicinano a quella retta che, passando per
confondendosi con il grafico divenuto approssimativamente lineare di f. Possiamo ben dire quindi che tali rette si avvicinano a quella retta che, passando per ![]() , approssima nel modo migliore l’andamento di f cioè la retta tangente. Contemporaneamente
, approssima nel modo migliore l’andamento di f cioè la retta tangente. Contemporaneamente
sembra diminuire la variabilità del loro coefficiente angolare:
il rapporto incrementale della funzione pare quindi convergere. A scala ancora maggiore queste osservazioni appaiono sempre più confermate e indipendentemente dal segno dell’incremento.
Per analizzare con maggior precisione la variabilità del rapporto incrementale conviene passare al suo calcolo numerico esplicito. Nella tabella seguente si sono quindi calcolati 100 rapporti incrementali sia in intorni destri che sinistri di ![]() a partire da un incremento massimo unitario (in valore assoluto). Il più piccolo incremento è quindi, in valore assoluto, pari a 0.01.
a partire da un incremento massimo unitario (in valore assoluto). Il più piccolo incremento è quindi, in valore assoluto, pari a 0.01.
Nella tabella le coppie (incremento, rapporto incrementale) sono ordinate secondo il valore decrescente del valore assoluto dell'incremento h in modo da poter osservare più facilmente la convergenza del rapporto incrementale al diminuire (del valore assoluto) di h.
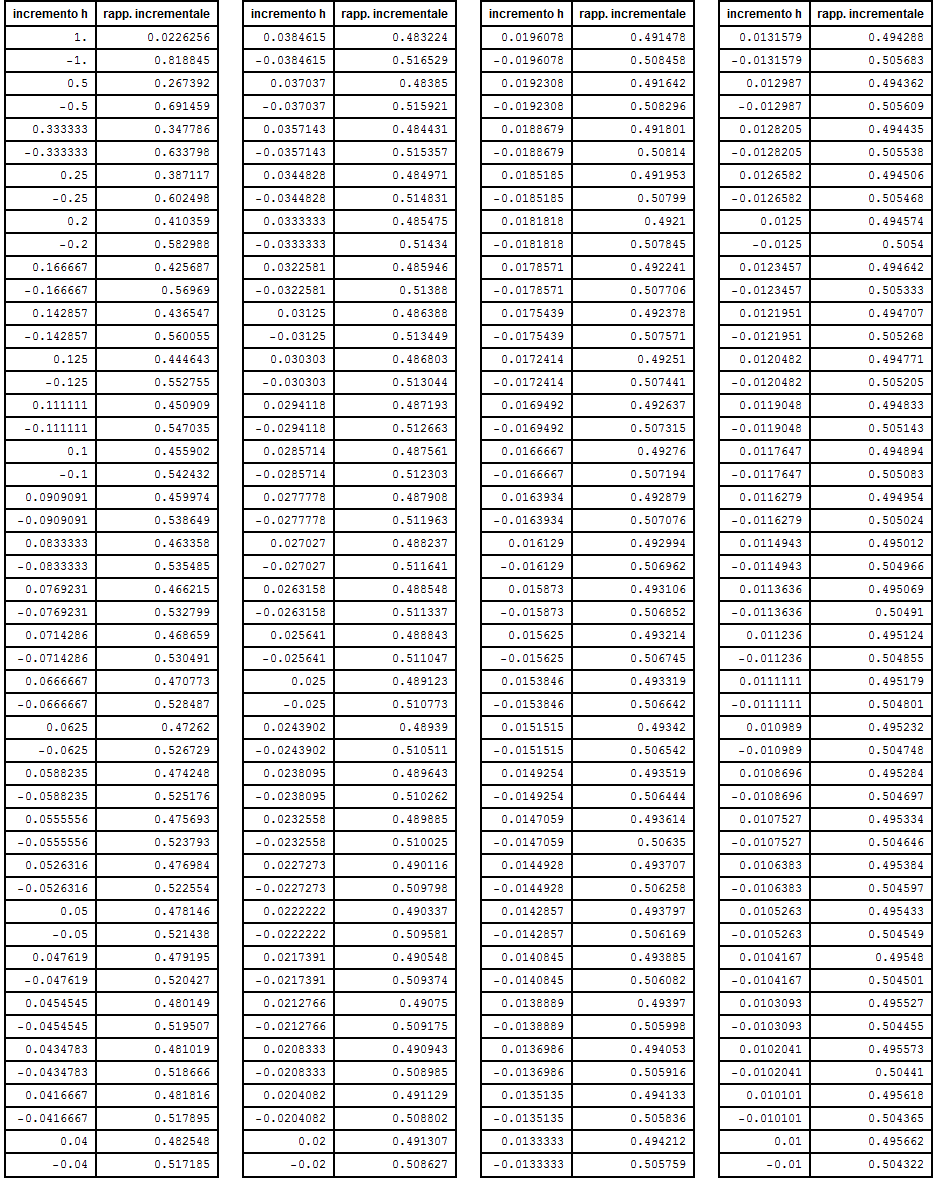
La rappresentazione grafica di questi coppie di valori mostra chiaramente la tendenza per il rapporto incrementale a convergere verso un determinato valore ( → 0.5) al tendere allo zero dell'incremento.
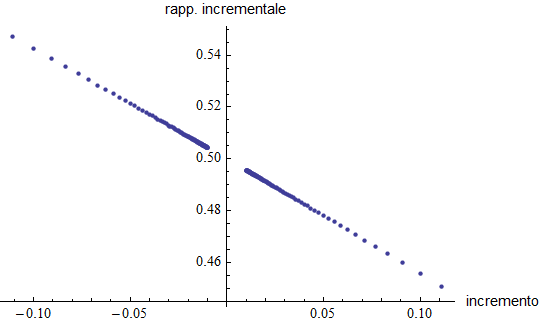
Per mostrare come nel caso della funzione g e nel punto di ascissa nulla l'andamento del rapporto incrementale sia totalmente diverso proponiamo lo stesso calcolo eseguito sopra per la f e nel quale l'intervallo iniziale di ampiezza unitaria (sia destra che sinistra) è stato gradualmente suddiviso in intervalli sempre più piccoli fino ad arrivare ad un valore minimo per l'incremento pari a ![]() .
.
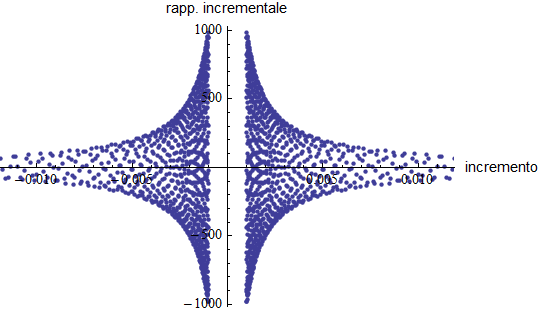
In questo caso possiamo ben dire come al tendere allo zero dell'incremento non esista un valore definito verso il quale il rapporto incrementale appaia convergere: anzi manifesta è la sua divergenza in valore assoluto.
Infine, per rendere l'esito del calcolo precedente ancora più esplicito forniamo una tabella dove assegnamo all'incremento h valori molto piccoli: corrispondentemente, il rapporto incrementale mostra chiaramente una convergenza verso il valore 0.5.
| incremento h | rapp. incrementale |
| 0.1 | 0.455902 |
| 0.01 | 0.495662 |
| 0.001 | 0.499567 |
| 0.0001 | 0.499957 |
| 0.00001 | 0.499996 |
| 1.*10^-6 | 0.5 |
| 1.*10^-7 | 0.5 |
| 1.*10^-8 | 0.5 |
| 1.*10^-9 | 0.5 |
| 1.*10^-10 | 0.5 |
Riprendendo la funzione g analizziamo pure per essa e per mezzo del calcolo l'andamento del rapporto incrementale in intorni, questa volta, del punto di ascissa 0.5.
| incremento h | rapp. incrementale |
| 0.1 | 0.861105 |
| 0.01 | 1.56162 |
| 0.001 | 1.65402 |
| 0.0001 | 1.66353 |
| 0.00001 | 1.66448 |
| 1.*10^-6 | 1.66458 |
| 1.*10^-7 | 1.66459 |
| 1.*10^-8 | 1.66459 |
| 1.*10^-9 | 1.66459 |
| 1.*10^-10 | 1.66459 |
Anche in questo caso emerge la convergenza del rapporto verso il valore 1.66459.
Concludiamo ripercorrendo per una terza funzione t lo studio, sia grafico che numerico, del rapporto incrementale. Definita la funzione come
uno zoom attorno al suo punto di ascissa 1 mostra
![]()
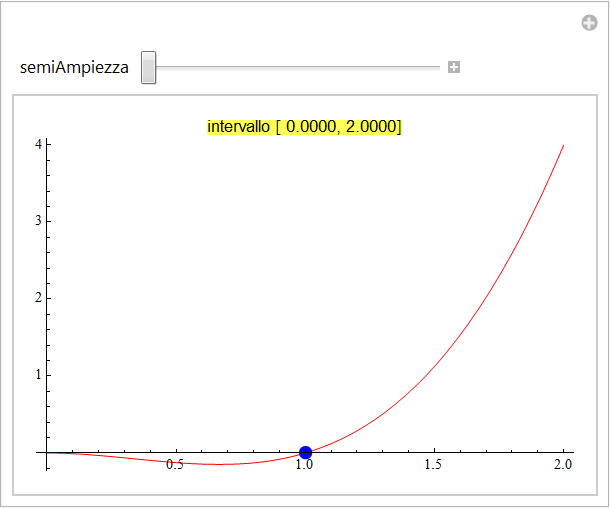
l'esistenza di un andamento approssimativamente lineare a piccola scala. Evidenziando il triangolo coinvolgente gli incrementi abbiamo
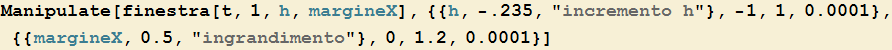
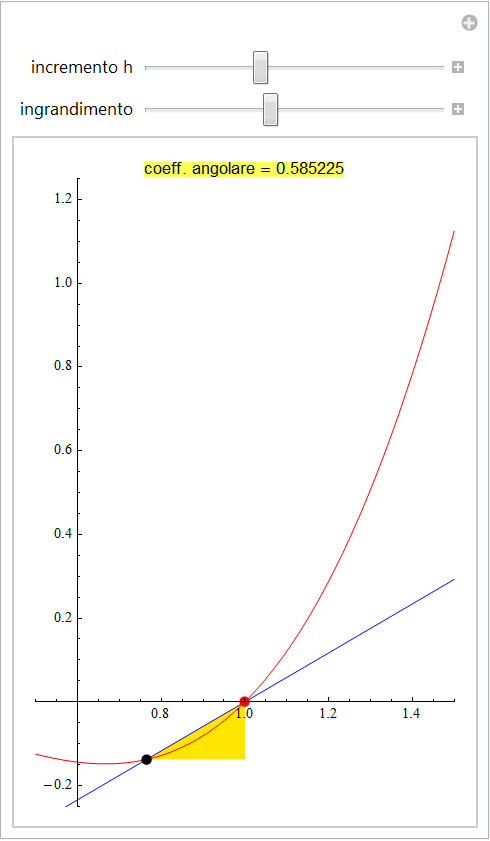
e la costanza del rapporto appare più evidente se si passa a scale più piccole.
Il calcolo numerico dei rapporti a partire da un incremento unitario per giungere al valore di ![]() fornisce la tabella seguente
fornisce la tabella seguente
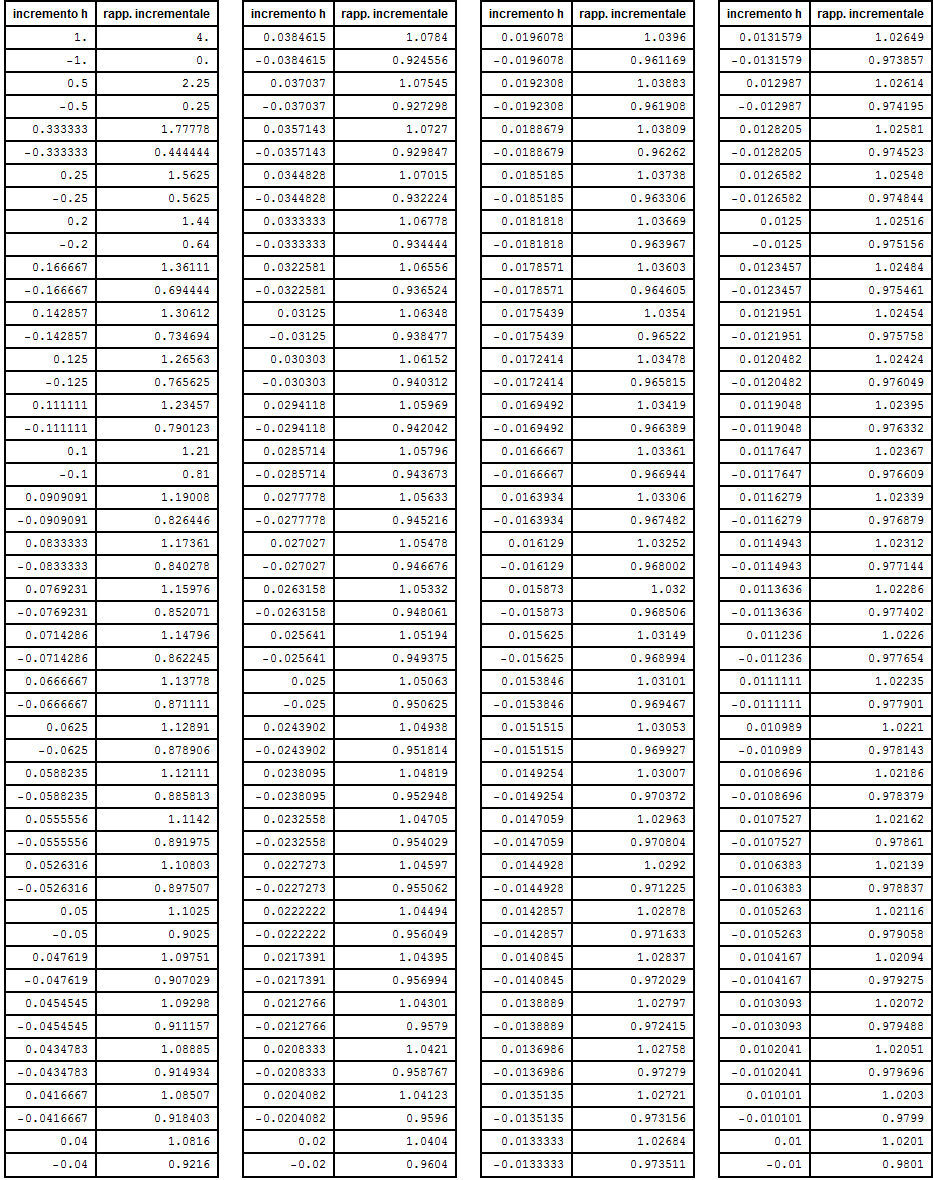
ben sintetizzata dalla rappresentazione grafica seguente: questa conferma visivamente la convergenza del rapporto verso l'unità.
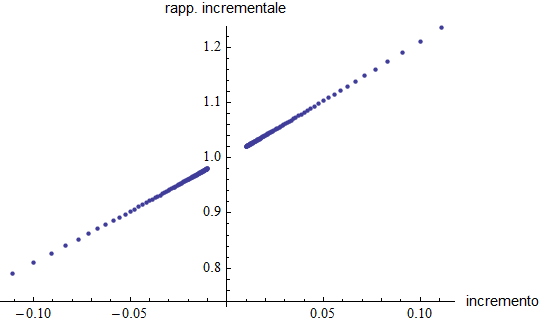
Diminuendo sensibilmente l'incremento, si ha infine
| incremento h | rapp. incrementale |
| 0.1 | 1.21 |
| 0.01 | 1.0201 |
| 0.001 | 1.002 |
| 0.0001 | 1.0002 |
| 0.00001 | 1.00002 |
| 1.*10^-6 | 1. |
| 1.*10^-7 | 1. |
| 1.*10^-8 | 1. |
| 1.*10^-9 | 1. |
| 1.*10^-10 | 1. |
risultato che ci permette di affermare come il rapporto incrementale, calcolato in intorni del punto ![]() , tenda al valore 1 al tendere allo zero dell'incremento.
, tenda al valore 1 al tendere allo zero dell'incremento.
In definitiva possiamo riassumere l'esito della nostra analisi nelle osservazioni seguenti (già parzialmente esposte in precedenza) e relative alle proprietà caratterizzanti solo determinati punti delle funzioni studiate:
dal punto di vista geometrico: al tendere del punto P a ![]() , le rette secanti approssimano sempre meglio l’andamento della funzione f confondendosi con il suo grafico approssimativamente lineare. Queste rette si avvicinano ad una retta limite (la tangente) che, passante per
, le rette secanti approssimano sempre meglio l’andamento della funzione f confondendosi con il suo grafico approssimativamente lineare. Queste rette si avvicinano ad una retta limite (la tangente) che, passante per ![]() , approssima nel modo migliore l’andamento di f:
, approssima nel modo migliore l’andamento di f:
dal punto di vista numerico: al tendere allo 0 dell’incremento h, la variabilità del rapporto incrementale diminuisce e questo mostra di convergere ad un ben preciso limite.
Definizione di derivata in un punto
Nelle precedenti sezioni abbiamo fornito la definizione di rapporto incrementale di una funzione in un suo punto e studiato il suo andamento sia tramite la grafica che numericamente. Tutto ciò giustifica, almeno a livello intuitivo, la definizione seguente:
Definizione. Si definisce derivata di una funzione f in un suo punto ![]() il limite, se esiste finito, del rapporto incrementale, al tendere allo zero dell’incremento h.
il limite, se esiste finito, del rapporto incrementale, al tendere allo zero dell’incremento h.
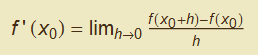 con
con ![]()
Poiché poi, a livello geometrico, la retta tangente nel punto ![]() del grafico della funzione f viene definita come il limite, se esiste, della retta secante al tendere del punto
del grafico della funzione f viene definita come il limite, se esiste, della retta secante al tendere del punto ![]() a
a ![]() ossia al tendere allo zero di h, possiamo identificare la derivata in
ossia al tendere allo zero di h, possiamo identificare la derivata in ![]() come il coefficiente angolare della retta tangente. L'equazione di questa retta è, nell'ipotesi di esistenza del limite dato sopra,
come il coefficiente angolare della retta tangente. L'equazione di questa retta è, nell'ipotesi di esistenza del limite dato sopra,
![]()
Esempi di calcolo formale di derivate
Procediamo in questa sezione al calcolo formale della derivata delle tre funzioni che abbiamo studiato precedentemente.
Per la funzione f nel punto ![]() il rapporto incrementale risulta
il rapporto incrementale risulta
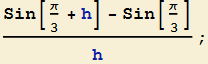
e se si usano le formule di prostaferesi per il seno si può fattorizzare a numeratore un termine del tipo ![]() .
.
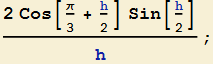
Quest'ultima si può riscrivere come
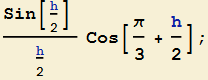
per cui tenendo conto del primo limite fondamentale e della continuità del coseno, il limite di tale espressione fornisce
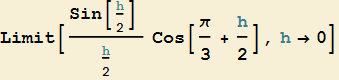
![]()
in accordo con quanto ottenuto numericamente.
Per la funzione t calcoliamo, inizialmente nel punto generico di ascissa ![]() , il rapporto incrementale
, il rapporto incrementale
![]()
![]()
Eseguendo i quadrati e raccogliendo i fattori comuni si ottiene per il numeratore
![]()
![]()
per cui semplificando discende
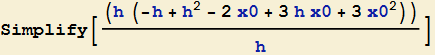
![]()
Volendo la derivata nel punto ![]() , si sostituisce questo valore ad
, si sostituisce questo valore ad ![]() giungendo a
giungendo a
![]()
![]()
ed eseguendo il limite di tale argomento per h→0 appare immediato ottenere
![]()
![]()
che è il valore pure aspettato.
Passiamo infine al calcolo del limite del rapporto incrementale per la funzione g nel punto ![]() . Il rapporto incrementale nel punto di ascissa
. Il rapporto incrementale nel punto di ascissa ![]() risulta
risulta
![]()
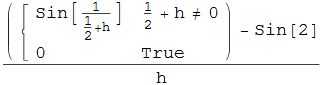
che, tramite le formule di prostaferesi, si riscrive come
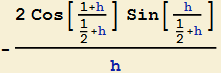
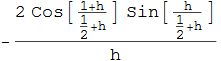
Volendo trattare separatamente i termini 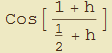 e
e 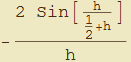 , introduciamo per il solo secondo fattore, la nuova variabile
, introduciamo per il solo secondo fattore, la nuova variabile 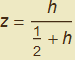 da cui h
da cui h
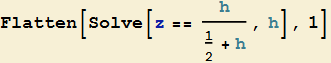
![]()
Il termine 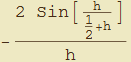 assume di conseguenza la forma più semplice
assume di conseguenza la forma più semplice
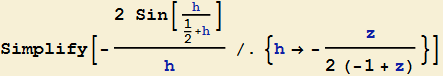
![]()
e il suo limite è
![]()
![]()
L'altro fattore del rapporto incrementale conduce al limite
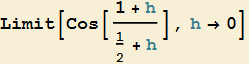
![]()
per cui in definitiva si ha
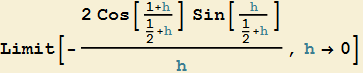
![]()
Numericamente tale limite equivale a
![]()
![]()
che coincide con quanto già trovato precedentemente per altra via.
Ritorna alla pagina di presentazione