Argomenti di Geometria Analitica
Le coniche
Sfruttando il software di geometria dinamica GeoGebra, si propongono le principali e classiche costruzioni geometriche delle coniche associando ad alcune di esse pure la deduzione formale della corrispondente equazione canonica. Ciascuna conica viene anche ottenuta come inviluppo di una famiglia di rette tangenti, dapprima costruita geometricamente e, successivamente, esplicitata in forma analitica. Per la comprensione di quest'ultima parte sarà necessario disporre dei concetti di limite e di derivata.
Curve celebri
Quale estensione dei metodi applicati nello studio delle coniche si propongono dei percorsi di approfondimento che, in aggiunta alle costruzioni di carattere geometrico di alcune tra le più importanti curve della storia della matematica, intendono ottenere anche le loro principali rappresentazioni analitiche.
MATEpristem (Università Bocconi)
Il sito del Centro PRISTEM dell'Università Bocconi di Milano ha recentemente pubblicato un mio articolo dal titolo “Famiglie di curve e inviluppi” nel quale riprendo in forme più mirate alcuni aspetti didattici sviluppati nelle pagine che da questa hanno origine. Di seguito fornisco quindi un file contenente i materiali citati nell'articolo: questi sono costituiti dai file di GeoGebra relativi alle diverse costruzioni e quelli che presentano le soluzioni simboliche dei sistemi algebrici coinvolti.
Note tecniche
File sorgenti ggb. Per rendere più agile la consultazione si è scelto di inserire nelle diverse pagine le sole immagini statiche riprese dai sorgenti in formato ggb di GeoGebra. Per poter accedere a questi file devono essere innanzitutto salvati localmente così da poter riprodurre personalmente e passo passo la costruzione e/o modificarli. A tal fine è sufficiente un clic sull'immagine stessa o sulla sua didascalia per avviarne il prelievo.
Formule matematiche. In entrambi i casi le espressioni matematiche presenti nelle pagine che da qui si diramano sono scritte in linguaggio TeX (nello specifico, in plain TeX) e utilizzano la tecnologia di MathJax, software scritto in JavaScript e interpretato correttamente da tutti i browser più recenti. Questa applicazione consente di ottenere un'ottima qualità nella resa tipografica: per esempio, le formule si possono ingrandire senza perdere in definizione mentre ciò non succede con formule costituite da immagini. Il caricamento dei font matematici, trasparente all'utente che consulta la pagina, avviene però con il collegamento ad un server esterno per cui si dovrà attendere solo qualche secondo perché il browser riporti correttamente le formule inserite nella pagina. Per tale motivo deve essere attivo un collegamento alla Rete.
Nello spazio sottostante riportiamo una formula d'esempio accanto alla corrispondente immagine della stessa in modo da poter verificare il corretto funzionamento.
| MathJax (ok) | immagine | |
|---|---|---|
| \[\cases{x={2a\sin t\over 1+\cos^2t}\cr\cr y={2a\sin t\cos t\over 1+\cos^2t}\cr}\] | 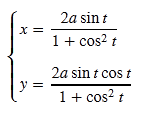
|
Nel caso invece non sia presente il collegamento alla rete si otterrà in un riquadro solo la linea con le istruzioni TeX.
\[\cases{x={2a\sin t\over 1+\cos^2t}\cr\cr y={2a\sin t\cos t\over 1+\cos^2t}\cr}\]
Infine un clic destro del mouse sulla formula apre il menu contestuale sottostante. Questo permette di ottenere in una finestra a parte i comandi TeX esportabili in un editor (Show Math As/TeX Commands) oppure, tra gli altri, lo zoom della singola formula (Math Settings/Zoom Trigger/Hover).