| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. |
In questa pagina intendiamo presentare le più semplici costruzioni ottenibili con riga e compasso allo scopo di comprendere l'uso degli strumenti di base presenti nei programmi interattivi di geometria così come, ovviamente, di ripassare alcune elementari proprietà geometriche. Per alcune di queste costruzioni presenteremo più modalità in modo da disporre di un più ampio ventaglio di strumenti.
Dalla
segue facilmente pure il teorema
In base a questa proprietà potremo tracciare l'asse se individuiamo due punti qualsiasi che siano equidistanti dagli estremi. Definiti quindi con lo strumento segmento ![]() gli estremi A e B del segmento (fig. 1), puntando su A con raggio AB si tracci la circonferenza c1 tramite
gli estremi A e B del segmento (fig. 1), puntando su A con raggio AB si tracci la circonferenza c1 tramite ![]() e, puntando su B si tracci, con il medesimo raggio, la circonferenza c2. Individuate le intersezioni P e Q di c1 e c2 tramite
e, puntando su B si tracci, con il medesimo raggio, la circonferenza c2. Individuate le intersezioni P e Q di c1 e c2 tramite ![]() (è sufficiente posizionare il mouse in vicinanza dei punti di intersezione e Z.u.L. evidenzia sia il punto che le curve coivolte), questi punti sono, per costruzione, equidistanti dagli estremi del segmento: è sufficiente tracciare la retta per essi
(è sufficiente posizionare il mouse in vicinanza dei punti di intersezione e Z.u.L. evidenzia sia il punto che le curve coivolte), questi punti sono, per costruzione, equidistanti dagli estremi del segmento: è sufficiente tracciare la retta per essi ![]() per ottenere l'asse di AB.
per ottenere l'asse di AB.
È evidentemente possibile eseguire la medesima costruzione costruendo le due circonferenze con un raggio qualsiasi purché maggiore della semilunghezza del segmento AB. Inoltre si tenga presente che questa stessa costruzione permette di determinare il punto medio M di un segmento: per ottenerlo basta intersecare AB con l'asse appena costruito. Pertanto lo strumento punto medio ![]() proposto in qualsiasi programma di geometria dinamica, non rappresenta che una comoda scorciatoia a questa costruzione.
proposto in qualsiasi programma di geometria dinamica, non rappresenta che una comoda scorciatoia a questa costruzione.
figura 1
Nel caso si intenda riprodurre personalmente la costruzione conviene innanzitutto analizzare quanto già proposto selezionando il tasto Ripeti costruzione ![]() (passare con il mouse sopra le icone e fermarsi per qualche istante per riconoscerne la funzione). Premendolo ancora nella piccola finestra Ripeti che in tal modo appare, questo strumento permette di ripercorrere gradualmente la successione degli elementi via via aggiunti e il significato dei quali viene riportato nella riga inferiore di stato della finestra del browser.
(passare con il mouse sopra le icone e fermarsi per qualche istante per riconoscerne la funzione). Premendolo ancora nella piccola finestra Ripeti che in tal modo appare, questo strumento permette di ripercorrere gradualmente la successione degli elementi via via aggiunti e il significato dei quali viene riportato nella riga inferiore di stato della finestra del browser.
Quindi, chiusa la finestra Ripeti e prima di procedere alla costruzione, vanno cancellati gli elementi presenti premendo più volte il tasto back ![]() fino a cancellare tutte le immissioni oppure, più brevemente, con il tasto
fino a cancellare tutte le immissioni oppure, più brevemente, con il tasto ![]() che cancella un oggetto e tutti gli elementi che da questo dipendono.
che cancella un oggetto e tutti gli elementi che da questo dipendono.
Se si commette un errore durante la costruzione, si può ripristinare la situazione appena precedente con il tasto back ![]() mentre se si intende ritornare nella situazione iniziale con la figura completa va ricaricata l'intera pagina. Pertanto nel browser che si sta utilizzando va selezionato il tasto Aggiorna
mentre se si intende ritornare nella situazione iniziale con la figura completa va ricaricata l'intera pagina. Pertanto nel browser che si sta utilizzando va selezionato il tasto Aggiorna ![]() .
.
Infine, si può ovviamente procedere alla costruzione selezionando il tasto Start in fondo alla pagina. Verrà presentato, in una finestra a sé stante, l'intero apparato degli strumenti di Z.u.L. ma con le restrizioni già esposte precedentemente: in tal caso ridimensionando questa finestra o spostandola si può mantenere in vista la figura originaria.
Per costruire, ad una retta data r, la perpendicolare p passante per un punto P vanno considerate le due possibilità
Nel primo caso, riportata la retta r con lo strumento linea ![]() sia P uno dei due punti appena definiti. Tracciamo quindi una circonferenza di centro P e raggio arbitrario
sia P uno dei due punti appena definiti. Tracciamo quindi una circonferenza di centro P e raggio arbitrario ![]() e definiamo i punti A e B di intersezione tra questa e r
e definiamo i punti A e B di intersezione tra questa e r ![]() . Possiamo ora procedere come nella costruzione precedente per ottenere l'asse di AB che rappresenta pure la retta p cercata.
. Possiamo ora procedere come nella costruzione precedente per ottenere l'asse di AB che rappresenta pure la retta p cercata.
Nel caso P non appartenga alla retta data (fig. 2), tracciamo una circonferenza di centro P e raggio opportuno ![]() così da poter individuare le sue intersezioni
così da poter individuare le sue intersezioni ![]() , A e B, con r. Successivamente tracciamo altre due circonferenze di raggio AP = BP centrate in A e in B. Il punto di intersezione Q tra queste ultime
, A e B, con r. Successivamente tracciamo altre due circonferenze di raggio AP = BP centrate in A e in B. Il punto di intersezione Q tra queste ultime ![]() e che si affianca a P permette di ottenere, con lo strumento
e che si affianca a P permette di ottenere, con lo strumento ![]() , la retta perpendicolare p.
, la retta perpendicolare p.
In aggiunta a ciò, il punto Q in tal modo ottenuto rappresenta il punto simmetrico a P rispetto a retta data r.
figura 2
Osserviamo ancora che lo strumento Linea perpendicolare ![]() , proposto anch'esso nei programmi di geometria, costituisce una comoda abbreviazione di quanto appena esposto e, data la sua importanza, verrà utilizzato frequentemente in queste pagine.
, proposto anch'esso nei programmi di geometria, costituisce una comoda abbreviazione di quanto appena esposto e, data la sua importanza, verrà utilizzato frequentemente in queste pagine.
Basandoci sulla sola definizione di asse di un segmento disponiamo oramai degli strumenti che ne permettono una costruzione diretta. Difatti lo strumento ![]() fornisce il punto medio di un segmento mentre
fornisce il punto medio di un segmento mentre ![]() la retta perpendicolare per un punto. La
costruzione quindi segue immediata (fig. 3).
la retta perpendicolare per un punto. La
costruzione quindi segue immediata (fig. 3).
figura 3
Quanto appena descritto può servire pure per costruire un triangolo equilatero di lato assegnato. La procedura che segue, in effetti, appare come la prima costruzione descritta da Euclide nel libro I dei suoi Elementi.
Definiti quindi con lo strumento segmento ![]() gli estremi A e B del segmento (fig. 4), puntando su A con raggio AB si tracci la circonferenza c1 tramite
gli estremi A e B del segmento (fig. 4), puntando su A con raggio AB si tracci la circonferenza c1 tramite ![]() e, puntando su B si tracci, con il medesimo raggio, la circonferenza c2. Individuate le intersezioni C e D di c1 e c2 tramite
e, puntando su B si tracci, con il medesimo raggio, la circonferenza c2. Individuate le intersezioni C e D di c1 e c2 tramite ![]() , queste sono per costruzione, equidistanti dagli estremi del segmento e in particolare risulta AB = BC = CA.
, queste sono per costruzione, equidistanti dagli estremi del segmento e in particolare risulta AB = BC = CA. ![]() ABC è evidentemente equilatero.
ABC è evidentemente equilatero.
figura 4
Dalla
discende immediatamente il
In base a questa proprietà, siamo in grado di eseguire, con riga e compasso, la costruzione della bisettrice.
Costruito l'angolo r1Or2 per mezzo dello strumento semiretta ![]() di vertice O (fig. 5), tracciamo una circonferenza di centro O che interseca i lati r1 e r2 in A e in B, rispettivamente. Si noti che si è scelto di attivare una visualizzazione parziale della circonferenza. Per ottenere ciò è sufficiente selezionare il pulsante Edita oggetto
di vertice O (fig. 5), tracciamo una circonferenza di centro O che interseca i lati r1 e r2 in A e in B, rispettivamente. Si noti che si è scelto di attivare una visualizzazione parziale della circonferenza. Per ottenere ciò è sufficiente selezionare il pulsante Edita oggetto ![]() e fare clic sull'oggetto per modificarne le proprietà nel riquadro che viene presentato. In tal caso si è selezionata l'opzione cerchi parziali
e fare clic sull'oggetto per modificarne le proprietà nel riquadro che viene presentato. In tal caso si è selezionata l'opzione cerchi parziali ![]() . Poi, puntando dapprima in A e poi in B e con raggio AB, tracciamo le due circonferenze che hanno in comune il punto C. La semiretta di origine O e passante per C è la bisettrice cercata.
. Poi, puntando dapprima in A e poi in B e con raggio AB, tracciamo le due circonferenze che hanno in comune il punto C. La semiretta di origine O e passante per C è la bisettrice cercata.
Infatti, i due triangoli OAC e OBC sono congruenti avendo i tre lati ordinatamente congruenti in quanto OC in comune e OA = OB, AC = BC per costruzione. In particolare avremo ![]() AOC =
AOC = ![]() BOC.
BOC.
figura 5
In alternativa, determinati i due punti A e B, costruire il punto medio M del segmento AB (che possiamo anche non visualizzare) e poi unire O con M per ottenere la bisettrice (fig. 6).
figura 6
Come conseguenza del teorema di Talete riguardante un fascio di rette parallele tagliate da due trasversali è possibile suddividere un dato segmento in un numero qualunque di parti congruenti ossia di ottenere un sottomultiplo di un segmento.
Supponiamo di voler suddividere il segmento AB (fig. 7) in 5 parti congruenti. Considerata una qualunque semiretta r1 di origine A e formante un angolo diverso da quello piatto ![]() , riportiamo su di essa un punto C con lo strumento punto su un oggetto
, riportiamo su di essa un punto C con lo strumento punto su un oggetto ![]() . A partire da A con lo strumento compasso
. A partire da A con lo strumento compasso ![]() riportiamo altri 4 segmenti congruenti ad AC cioè CD, DE, EF, FG. Tracciata la retta per B e G, basta condurre le parallele ad essa
riportiamo altri 4 segmenti congruenti ad AC cioè CD, DE, EF, FG. Tracciata la retta per B e G, basta condurre le parallele ad essa ![]() per i punti C, D, E, F. Infine le loro intersezioni (utilizzare
per i punti C, D, E, F. Infine le loro intersezioni (utilizzare ![]() per individuarle e definirle), per il teorema di Talete, suddividono il segmento originario AB in sottomultipli congruenti del rapporto voluto.
per individuarle e definirle), per il teorema di Talete, suddividono il segmento originario AB in sottomultipli congruenti del rapporto voluto.
Si tenga presente che i punti liberi della costruzione sono A, B e C.
figura 7
Ne segue il
Evidentemente il circocentro è equidistante dai vertici del triangolo: è quindi facile in base a queste proprietà individuare il circocentro e costruire la circonferenza circoscritta. Difatti costruito il triangolo ABC ![]() (fig. 8), si trovano i punti medi P, Q ed R dei tre lati
(fig. 8), si trovano i punti medi P, Q ed R dei tre lati ![]() . Tracciate le tre perpendicolari ai lati passanti per i punti medi tramite
. Tracciate le tre perpendicolari ai lati passanti per i punti medi tramite ![]() (si seleziona prima la retta o il segmento e quindi il punto), l'intersezione di due di esse individua il circocentro O. Infine con lo strumento circonferenza, puntando su O e con raggio OA, si costruisce la circonferenza circoscritta.
(si seleziona prima la retta o il segmento e quindi il punto), l'intersezione di due di esse individua il circocentro O. Infine con lo strumento circonferenza, puntando su O e con raggio OA, si costruisce la circonferenza circoscritta.
figura 8
Ne segue che l'incentro è equidistante dai tre lati del triangolo per cui la circonferenza che ha questo punto come centro ed è tangente ai tre lati del triangolo, è la circonferenza inscritta. Per ottenerla vanno costruite innanzitutto le bisettrici ai tre angoli interni ad un triangolo ABC (o almeno a due di essi). Per far ciò conviene tracciare il triangolo con lo strumento linea ![]() così da disporre delle rette AB, BC e CA (fig. 9). Individuato l'incentro I come intersezione di una qualsiasi coppia di bisettrici va definito il raggio. Per determinarlo costruire la perpendicolare ad un lato qualsiasi passante per I (attivato
così da disporre delle rette AB, BC e CA (fig. 9). Individuato l'incentro I come intersezione di una qualsiasi coppia di bisettrici va definito il raggio. Per determinarlo costruire la perpendicolare ad un lato qualsiasi passante per I (attivato ![]() si seleziona prima la retta e poi il punto) per cui, detta P la loro intersezione, il raggio è pari alla lunghezza di PI.
si seleziona prima la retta e poi il punto) per cui, detta P la loro intersezione, il raggio è pari alla lunghezza di PI.
figura 9
Si noti che nella costruzione precedente si sono nascoste alcune parti della costruzione tramite lo strumento nascondi ![]() . Le stesse possono essere ripristinate selezionando il tasto di mostra/nascondi oggetti nascosti
. Le stesse possono essere ripristinate selezionando il tasto di mostra/nascondi oggetti nascosti ![]() . Quest'ultimo quindi attiva o disattiva la visualizzazione di oggetti nascosti. Inoltre, in presenza di oggetti nascosti, se si intende avviare la ripetizione della costruzione con
. Quest'ultimo quindi attiva o disattiva la visualizzazione di oggetti nascosti. Inoltre, in presenza di oggetti nascosti, se si intende avviare la ripetizione della costruzione con ![]() , conviene preventivamente attivare la visualizzazione di tutti gli oggetti nascosti tramite
, conviene preventivamente attivare la visualizzazione di tutti gli oggetti nascosti tramite ![]() . In tal modo si potranno seguire tutti i passi effettivamente seguiti.
. In tal modo si potranno seguire tutti i passi effettivamente seguiti.
Costruito un triangolo ABC tramite lo strumento linee ![]() , possiamo definire pure le bisettrici degli angoli esterni ossia degli angoli formati da un lato del triangolo e dal prolungamento degli altri due (fig. 10).
, possiamo definire pure le bisettrici degli angoli esterni ossia degli angoli formati da un lato del triangolo e dal prolungamento degli altri due (fig. 10).
figura 10
Pertanto, procedendo come già esposto le bisettrici si intersecano nei punti P, Q ed R, tutti esterni al triangolo. Questi, per la proprietà delle bisettrici sono equidistanti dal lato e dai prolungamenti degli altri due, per cui sono i centri di altrettante circonferenze. Per determinare il raggio basta tracciare la perpendicolare ai lati passante per questi punti (detti ex-centri) e individuarne l'intersezione con il lato. La lunghezza di questo segmento è il raggio della circonferenza che quindi si può costruire. Analogamente si procede per le rimanenti due circonferenze ex-inscritte.
Per ulteriori proprietà e teoremi si veda la pagina sulle circonferenze inscritta ed ex-inscritte.
figura 11
Una ben nota proprietà delle altezze di un triangolo stabilisce (fig. 12)
figura 12
mentre per le mediane, un'altrettanto nota proprietà afferma che
La costruzione di questi punti e la sperimentazione visiva di questi teoremi è immediata. Nella successiva figura 13 proponiamo invece una verifica numerica della seconda parte del precedente teorema.
A tal fine si fa uso dello strumento espressione aritmetica ![]() che permette di inserire e calcolare espressioni coinvolgenti distanze, aree, angoli ed altre funzioni dipendenti dagli elementi della costruzione (passando pertanto dalla geometria sintetica a quella algebrica). Nel nostro caso vogliamo confrontare numericamente la misura della lunghezza del segmento AG con il doppio di GQ (fig. 13).
che permette di inserire e calcolare espressioni coinvolgenti distanze, aree, angoli ed altre funzioni dipendenti dagli elementi della costruzione (passando pertanto dalla geometria sintetica a quella algebrica). Nel nostro caso vogliamo confrontare numericamente la misura della lunghezza del segmento AG con il doppio di GQ (fig. 13).
Poiché questi segmenti non sono ancora stati definiti in modo esplicito (lo sono i loro estremi ma solo come punti) converrà selezionare lo strumento segmento ![]() e definire i segmenti AG e GQ. Fatto ciò ci si deve assicurare del nome con il quale il programma li individua. A tal fine basta un clic con il tasto destro del mouse su di essi e scegliere, dalla lista che appare l'elemento che inizia con la lettera s (potrebbe essere s1 e/o s2). In alternativa, la selezione del tasto F11 permette di accedere ad un elenco di tutti gli elementi della costruzione finora eseguita e selezionarli). Assicuratici del nome che appare in corrispondenza della cella Text possiamo ora nascondere alla vista
e definire i segmenti AG e GQ. Fatto ciò ci si deve assicurare del nome con il quale il programma li individua. A tal fine basta un clic con il tasto destro del mouse su di essi e scegliere, dalla lista che appare l'elemento che inizia con la lettera s (potrebbe essere s1 e/o s2). In alternativa, la selezione del tasto F11 permette di accedere ad un elenco di tutti gli elementi della costruzione finora eseguita e selezionarli). Assicuratici del nome che appare in corrispondenza della cella Text possiamo ora nascondere alla vista ![]() il segmento non essendo un elemento importante per la costruzione. Si ripeta ciò per entrambi i segmenti.
il segmento non essendo un elemento importante per la costruzione. Si ripeta ciò per entrambi i segmenti.
Selezionare ora il tasto espressione ![]() e quindi si punti con un clic dove intendiamo collocare la misura. Nella finestra che appare, in corrispondenza della cella Espressione aritmetica immettere il nome del segmento (per esempio s1) mentre in corrispondenza di Spiegazione inserire, per esempio, lunghezza di AG. Procedere analogamente per il segmento (probabilmente s2) GQ immettendo però la formula 2*s2 e come spiegazione 2 GQ.
e quindi si punti con un clic dove intendiamo collocare la misura. Nella finestra che appare, in corrispondenza della cella Espressione aritmetica immettere il nome del segmento (per esempio s1) mentre in corrispondenza di Spiegazione inserire, per esempio, lunghezza di AG. Procedere analogamente per il segmento (probabilmente s2) GQ immettendo però la formula 2*s2 e come spiegazione 2 GQ.
figura 13
Spostando qualsiasi vertice del triangolo sarà infine possibile controllare l'uguaglianza di questi due valori confermando l'affermazione del teorema.
Data la circonferenza di centro O e il punto P fuori di essa (fig. 14), per tracciare la tangente per P alla circonferenza va determinato, ovviamente, il punto di tangenza.
figura 14
Questo (o questi, visto che sono due) lo si determina dopo che si sia tracciata la circonferenza che ha come diametro il segmento OP. Difatti, selezionato lo strumento punto medio ![]() , si costruisce prima il punto medio M di OP e quindi, con il pulsante circonferenza
, si costruisce prima il punto medio M di OP e quindi, con il pulsante circonferenza ![]() , si ottiene la circonferenza di diametro OP. Le intersezioni
, si ottiene la circonferenza di diametro OP. Le intersezioni ![]() A e B di questa con la circonferenza originaria sono i punti di tangenza in quanto i triangoli
A e B di questa con la circonferenza originaria sono i punti di tangenza in quanto i triangoli ![]() PAO e
PAO e ![]() PBO sono rettangoli (in A e in B) perché inscritti in una semicirconferenza. PA e PB sono pertanto le rette tangenti cercate.
PBO sono rettangoli (in A e in B) perché inscritti in una semicirconferenza. PA e PB sono pertanto le rette tangenti cercate.
Questa semplice costruzione può rivelarsi utile nelle situazioni che mostrano una dipendenza da un angolo o dalla sua variazione oppure per poter generalizzare costruzioni nelle quali, in origine, intervenga un particolare angolo.
figura 15
Sia quindi dato l'angolo ![]() AOB, con O vertice e A e B due punti dei lati ottenuti come intersezioni della circonferenza di centro O e raggio arbitrario; è pertanto OA = OB. Sia pure data la semiretta r3 di origine P. Con lo strumento Circonferenza per 3 punti
AOB, con O vertice e A e B due punti dei lati ottenuti come intersezioni della circonferenza di centro O e raggio arbitrario; è pertanto OA = OB. Sia pure data la semiretta r3 di origine P. Con lo strumento Circonferenza per 3 punti ![]()
Definiamo l'intersezione Q ![]() tra la circonferenza appena costruita con la semiretta di origine r3 e quindi, ripetiamo la medesima procedura per riportare la distanza AB, questa volta con centro in Q. Successivamente intersechiamo le due circonferenze ottenendo due punti ciascuno dei quali permette di disporre di un angolo congruente con quello dato. Infine tracciamo la semiretta che collega uno di questi punti con il vertice P.
tra la circonferenza appena costruita con la semiretta di origine r3 e quindi, ripetiamo la medesima procedura per riportare la distanza AB, questa volta con centro in Q. Successivamente intersechiamo le due circonferenze ottenendo due punti ciascuno dei quali permette di disporre di un angolo congruente con quello dato. Infine tracciamo la semiretta che collega uno di questi punti con il vertice P.
Utilizzare lo strumento Ripeti costruzione ![]() per ripercorrere i passi descritti.
per ripercorrere i passi descritti.
Possiamo sfruttare quanto appena esposto per costruire la retta parallela p ad una data retta r, con p passante per un punto P non appartenente a r. Seguiranno quindi altre costruzioni con il medesimo obiettivo.
Costruzione 1. Riportata la retta r per due punti ![]() e il punto P
e il punto P ![]() esterno, sia A un qualsiasi punto di r. Tracciata la retta PA questa forma, nel semipiano contenente P e di origine r, una coppia di angoli supplementari. Dobbiamo ora riportare uno di questi sulla retta PA in modo che la retta parallela cercata formi con PA un angolo alterno interno congruente ad uno dei due.
esterno, sia A un qualsiasi punto di r. Tracciata la retta PA questa forma, nel semipiano contenente P e di origine r, una coppia di angoli supplementari. Dobbiamo ora riportare uno di questi sulla retta PA in modo che la retta parallela cercata formi con PA un angolo alterno interno congruente ad uno dei due.
Costruiamo quindi la circonferenza di centro A e raggio AP ![]() (fig. 16). Sia B una sua intersezione con r. Con il medesimo strumento aggiungiamo la circonferenza di centro P e raggio PA. Infine tramite lo strumento circonferenza per tre punti
(fig. 16). Sia B una sua intersezione con r. Con il medesimo strumento aggiungiamo la circonferenza di centro P e raggio PA. Infine tramite lo strumento circonferenza per tre punti ![]() costruire la circonferenza di raggio PB con centro in A (clic su P, su B, e infine, su A). L'intersezione Q tra queste due ultime circonferenze appartenente al semipiano di P di origine r congiunta con P
costruire la circonferenza di raggio PB con centro in A (clic su P, su B, e infine, su A). L'intersezione Q tra queste due ultime circonferenze appartenente al semipiano di P di origine r congiunta con P ![]() fornisce la retta p parallela ad r. Difatti la costruzione assicura la congruenza per gli angoli alterni interni
fornisce la retta p parallela ad r. Difatti la costruzione assicura la congruenza per gli angoli alterni interni ![]() BAP =
BAP = ![]() QPA.
QPA.
figura 16
Costruzione 2. Con centro nel punto P, tracciare una circonferenza con raggio sufficiente per intersecare in A la retta r ![]() (fig. 17). Riportare una seconda circonferenza avente centro in A e raggio AP e definirne B l'intersezione con r. Infine, con centro in B tracciare la circonferenza di raggio BA. L'intersezione di quest'ultima con quella di centro P (la prima delle tre) dà il punto Q che con P permette di ottenere la parallela voluta p. Avendo le tre circonferenze sempre il medesimo raggio, il quadrilatero ABQP risulta un rombo.
(fig. 17). Riportare una seconda circonferenza avente centro in A e raggio AP e definirne B l'intersezione con r. Infine, con centro in B tracciare la circonferenza di raggio BA. L'intersezione di quest'ultima con quella di centro P (la prima delle tre) dà il punto Q che con P permette di ottenere la parallela voluta p. Avendo le tre circonferenze sempre il medesimo raggio, il quadrilatero ABQP risulta un rombo.
figura 17
Costruzione 3. Consideriamo sulla linea rappresentativa di r due punti qualsiasi A, B (fig. 18). Colleghiamo con lo strumento segmento ![]() A con P e, determiniamo con
A con P e, determiniamo con ![]() il punto medio M di AP. Aggiungiamo alla figura finora ottenuta la retta MB
il punto medio M di AP. Aggiungiamo alla figura finora ottenuta la retta MB ![]() . Infine costruiamo il simmetrico di B rispetto al punto M per mezzo di una circonferenza di centro M e raggio MB
. Infine costruiamo il simmetrico di B rispetto al punto M per mezzo di una circonferenza di centro M e raggio MB ![]() : l'intersezione tra questa circonferenza e la retta MB, distinta da B, fornisce il punto Q
: l'intersezione tra questa circonferenza e la retta MB, distinta da B, fornisce il punto Q ![]() che con P, risolve il problema di tracciare la retta p.
che con P, risolve il problema di tracciare la retta p.
figura 18
Come in altre occasioni notiamo infine che lo strumento Linea parallela ![]() non rappresenta nient'altro che una comoda scorciatoia a queste costruzioni: nel seguito verrà sempre usato questo strumento.
non rappresenta nient'altro che una comoda scorciatoia a queste costruzioni: nel seguito verrà sempre usato questo strumento.
Nelle due immagini che concludono questa pagina riportiamo, solo come richiamo alla memoria, le elementari costruzioni del triangolo equilatero (e che verrà utilizzata nella pagina dedicata ai poligoni) e del quadrato, considerati come poligoni regolari inscritti in un cerchio di raggio assegnato.
Nel caso si intendano rivedere i diversi passaggi che conducono a queste costruzioni si selezioni la figura con il tasto destro del mouse e si scelga la voce Ripeti costruzione. Quindi utilizzare il tasto ![]() per scorrere i diversi elementi aggiunti ponendo attenzione alla breve descrizione proposta nella riga inferiore della finestra del browser.
per scorrere i diversi elementi aggiunti ponendo attenzione alla breve descrizione proposta nella riga inferiore della finestra del browser.
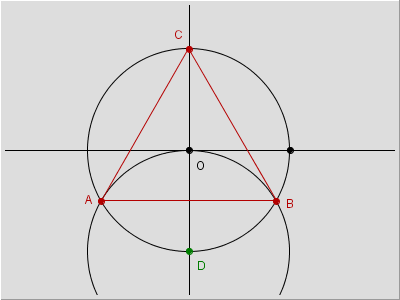
figura 19a |
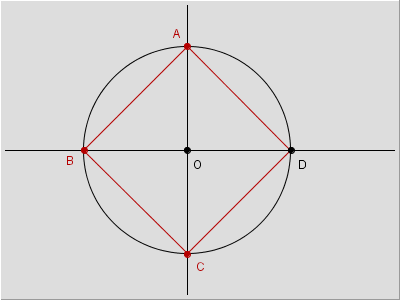
figura 19b |
| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. |
|
|||||||||||