Il teorema di G. Ceva e le sue conseguenze

Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb.

In questa pagina trattiamo di un teorema che fornisce una importante condizione sulla concorrenza di tre segmenti in uno stesso punto. In base ad esso si possono ritrovare risultati già noti della geometria elementare ma collocandoli in un ambito più generale. Dopo aver ripreso i teoremi sulla bisettrice di un angolo (sia interno che esterno), il teorema metrico di Stewart, dimostrato per mezzo del teorema trigonometrico di Carnot, permette di individuare la relazione che intercorre tra due lati di un triangolo e le parti in cui il terzo viene suddiviso da un qualsiasi "ceviano".

Il teorema di Ceva

Iniziamo con due definizioni

Definizione 1.

Un segmento che congiunge un vertice di un triangolo con un punto qualsiasi del lato opposto è detto segmento ceviano.

Definizione 2.

Tre rette o segmenti sono concorrenti se passano per lo stesso punto.

In base a queste posizioni, se P, Q, R sono punti appartenenti rispettivamente ai lati AB, BC, CA del ABC, i segmenti AQ, BR e CP sono ceviani. In particolare nella figura 1 i tre segmenti sono stati disegnati concorrenti nello stesso punto S, intersezione di AQ e BR (di conseguenza, solo i vertici del triangolo e i punti Q e R possono essere trascinati liberamente).

In tale situazione si può dimostrare l'interessante teorema del matematico italiano Giovanni Ceva (Milano 1647-Mantova 1734) e pubblicato da questi nel 1678.

Teorema di Ceva.

Se i tre segmenti ceviani AQ, BR e CP di ABC sono concorrenti, allora risulta

La dimostrazione segue facilmente una volta che si sia notato che le aree di triangoli con altezze congruenti sono proporzionali alle rispettive basi. Con riferimento alla figura 1 e in particolare al lato BC, abbiamo

dove, nella terza uguaglianza, si è utilizzata la proprietà che, dalla validità della proporzione

assicura pure la correttezza dei rapporti

Nota: la dimostrazione di quest'ultima proprietà è immediata se procediamo algebricamente: difatti da

discende subito a d = b c, per cui sommando ad entrambi i membri - c d otteniamo

da cui la tesi

Procedendo similmente sui lati CA e AB, si trova

Moltiplicando i rapporti a primo membro di ciascuna delle tre relazioni trovate si ottiene

come volevasi dimostrare.

Inverso del teorema di Ceva

Il teorema di Ceva possiede pure l'inverso:

Teorema (inverso).

Se tre segmenti ceviani AQ, BR, CP soddisfano alla relazione

AP PB

·

BQ QC

·

CR RA

= 1

allora essi sono concorrenti.

La dimostrazione si fa per assurdo supponendo che esista un punto P' distinto da P tale che, se i primi due segmenti ceviani si intersecano in S, il ceviano CP' passi attraverso S. In tal caso possiamo applicare il precedente teorema e ottenere

Dato che per ipotesi vale pure

ne discende

per cui P' deve coincidere con P contro l'ipotesi: i ceviani AQ, BR, CP sono pertanto concorrenti. In definitiva possiamo affermare che

Teorema.

Condizione necessaria e sufficiente affinché i tre segmenti ceviani AQ, BR e CP del ABC siano concorrenti, è che risulti

AP PB · BQ QC · CR RA  = 1

Per un'ulteriore estensione di tale asserzione si veda quanto esposto nella pagina riguardante il teorema di Menelao.

Verifica numerica

Di seguito presentiamo le istruzioni per ottenere una verifica numerica del teorema con il calcolo esplicito dell'espressione fondamentale del teorema eseguito in un applet di Z.u.L..

Costruita la figura geometrica con i tre ceviani concorrenti (fig. 2), selezionare l'icona espressione algebrica e fare un clic dove la si vuole inserire. Siccome dovremo immettere delle distanze tra punti, la sintassi da seguire è abbastanza semplice: se i punti sono, per esempio, A e P, allora la loro distanza si esprime come d(A,P). In sostanza, con i nomi dei punti dati in figura (che non sono quelli assegnati automaticamente da Z.u.L.) si immetta in corrispondenza delle celle Espressione Aritmetica e Spiegazione quanto riportato dalla sottostante figura (o con le modifiche del caso se i nomi non coincidono). 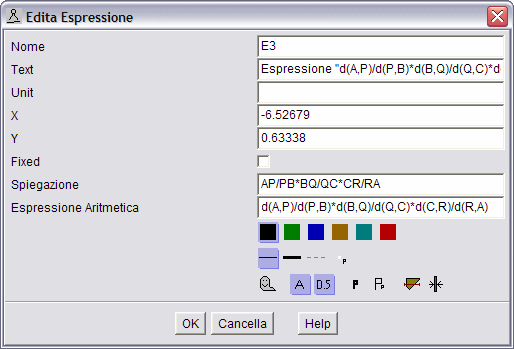Ricordarsi poi di attivarne la visualizzazione selezionando il tasto con la A della figura 3.

Con il tasto muovi si possono quindi muovere i tre vertici di ABC oppure i punti Q e R e osservare che, qualsiasi sia il triangolo o la scelta dei ceviani, il valore dell'espressione rimane costantemente pari ad 1.

Prime conseguenze: mediane e altezze

In base al teorema di Ceva segue immediatamente che le mediane di un triangolo sono concorrenti in un punto (che sappiamo essere il baricentro). Difatti è banale verificare che il prodotto è pari ad 1 se AP = PB, BQ = QC e CR = RA.

Vediamo, riferendoci alla figura 4, qualche altra conseguenza. Dal fatto che triangoli con la stessa base e altezza possiedono la medesima area, risulta

Sia a = (GBQ) = (GQC). Analogamente per

D'altra parte è pure

che implica a = b. Similmente (ABQ) = (AQC), da cui b = c. In definitiva è a = b = c e possiamo quindi enunciare il

Teorema.

Un triangolo viene suddiviso dalle mediane in 6 triangoli più piccoli di ugual area.

Ne segue anche (BGA) = 2(BQG) ma avendo BGA e BQG la medesima altezza (rispetto alle basi AG e GQ) si giunge alla ben nota proprietà delle mediane, AG = 2·GQ. Analogamente per le altre mediane (vedere più avanti in questa pagina per un'altra dimostrazione di questa proprietà).

Problema 1.1. Determinare il rapporto tra le aree di ABC con un triangolo avente per lati le tre mediane.
Soluzione

Un po' meno banale è la dimostrazione che le tre altezze di un triangolo (pure loro ceviani) si incontrano in uno stesso punto (che, ancora, sappiamo essere l'ortocentro). Difatti, in base alla figura seguente e alla definizione trigonometrica di coseno

risulta

Sostituendo queste espressioni nel primo membro della relazione di Ceva

AC cosA BC cosB

·

AB cosB AC cosC

·

BC cosC AB cosA

= 1

si vede facilmente che tutti i termini si semplificano fornendo 1 come risultato.

Poiché l'ortocentro può essere un punto esterno al triangolo conviene pure anticipare che il teorema di Ceva rimane valido anche in tal caso ossia quando i segmenti ceviani intersecano eventualmente i prolungamenti dei lati. Per la prova di ciò si veda la pagina sul teorema di Menelao.

Bisettrici

Anche le bisettrici di un triangolo si intersecano in un punto, l'incentro. Per dimostrarlo per mezzo del teorema di Ceva, conviene preventivamente ricordare (e dimostrare) un teorema elementare.

Teorema.

La bisettrice di un angolo interno di un triangolo divide il lato opposto all'angolo in parti proporzionali agli altri due lati e viceversa.

Dimostrazione 1. In base alla figura 6 dobbiamo dimostrare la correttezza del rapporto

Pertanto tracciata la parallela alla bisettrice AQ per B, BAT risulta isoscele sulla base BT in quanto BTA = QAC (angoli corrispondenti di rette parallele) e TBA = BAQ perché alterni interni di rette parallele. In particolare TA = AB. Per il teorema di Talete relativo ad un fascio di rette parallele vale la proporzione

ma per quanto detto TA = AB per cui discende la tesi.

Dimostrazione 2. Forniamo un'altra dimostrazione del teorema della bisettrice. In questa faremo uso del teorema trigonometrico dei seni che stabilisce (fig. 6)

BQ senBAQ

=

AB senBQA

QC senQAC

=

AC senAQC

Poiché

si ottiene rapportando ordinatamente il primo e il secondo membro

Dimostrazione dell'inverso. Supposto che sia

vogliamo dimostrare che è BAQ = QAC. Prolungato il lato CA di un segmento AT uguale a AB (fig. 6), TB risulta parallelo a AQ. Infatti, sostituendo nella proporzione dell'ipotesi al segmento AB il segmento congruente AT, questa diventa

dalla quale si deduce (per il teorema di Talete) BTAQ. Da ciò discendono le congruenze QAC = ATB (angoli corrispondenti di rette parallele) e BAQ = ABT (angoli alterni interni). D'altra parte, essendo AT = AB per costruzione, nel triangolo isoscele BAT risulta ABT = ATB per cui, per la transitività della congruenza, si ha BAQ = QAC c.v.d.

Riprendiamo il problema iniziale e passiamo a dimostrare l'incidenza delle tre bisettrici nell'incentro. Sempre con riferimento alla figura sopra e come conseguenza del teorema appena dimostrato possiamo ritenere validi i rapporti

cosicché il prodotto dei primi membri della relazione di Ceva diviene

manifestamente pari ad 1. Le tre bisettrici quindi sono concorrenti nell'incentro.

Infine, per completezza circa le proprietà delle bisettrici dimostriamo pure il seguente

Teorema

La bisettrice di un angolo esterno di un triangolo interseca il prolungamento del lato opposto in un punto le cui distanze dagli estremi di questo lato sono proporzionali agli altri due lati e viceversa.

Preso un punto qualsiasi R dalla parte opposta a B su BA (fig. 7) si ha per ipotesi

essendo P il punto d'incontro della bisettrice di RAC con il prolungamento di BC.

figura 7

Tracciata la parallela CQ ad AP per il teorema di Talete si ha la proporzione

Inoltre valgono le congruenze

AQC

=

RAP

QCA

=

CAP,

la prima perché angoli corrispondenti rispetto rette parallele, la seconda perché alterni interni rispetto alle stesse parallele. Ne segue che ACQ è isoscele con QA = CA. La proporzione iniziale può quindi scriversi

che è quanto volevamo dimostrare.
La dimostrazione dell'inverso è analoga a quella dell'inverso del teorema della bisettrice di un angolo interno. Comunque, in riferimento alla fig. 7, si costruisce un punto Q tale che QA = CA: AQC è perciò isoscele per costruzione. Dalla validità di

discende quella di

che in base al teorema di Talete implica il parallelismo di QC con AP. Ne seguono le congruenze

AQC

=

RAP

QCA

=

CAP

ma visto che AQC = QCA, per la proprietà transitiva, si ottiene CAP = RAP dalla quale discende che AP è la bisettrice dell'angolo esterno ad A c.v.d.

Problema 1.2. In ABC siano R (appartenente a BC), S (appartenente a CA) e T (appartenente a AB), i punti di tangenza della circonferenza inscritta. Dimostrare che i ceviani AR, BS e CT sono concorrenti.
Soluzione

Rapporto nel quale il punto di concorrenza divide ogni ceviano

Nel ABC, AQ, BR e CP sono dei ceviani concorrenti nel punto S (fig. 8ab).

figura 8a

figura 8b

All'inizio della dimostrazione del teorema di Ceva abbiamo stabilito i rapporti

Considerando ancora che le aree di triangoli aventi altezze congruenti sono nel medesimo rapporto delle basi possiamo aggiungere i seguenti

È quindi

Dagli ultimi due rapporti discende la validità pure di

dove, in base alla fig. 8a, si è utilizzata l'uguaglianza (SBQ) + (SQC) = (BCS). Le espressioni iniziali forniscono in definitiva

Nel caso rappresentato dalla fig. 8b il punto S appare esterno al triangolo. Pur in contrasto con quanto ipotizzato inizialmente ossia che i punti P, Q, R appartengano ai lati del triangolo ossia che il loro punto di concorrenza sia interno al triangolo, procediamo per completezza all'analisi pure di questa situazione in quanto, più avanti, tale limitazione verrà a cadere. Possiamo quindi scrivere

e pertanto, nel caso che i ceviani incidano in un punto esterno al triangolo, ottenere

Questi ultimi due rapporti risolvono il problema che ci eravamo posti.

Un esempio di tale risultato è immediato. Supposto che i tre segmenti ceviani coincidano con le mediane ai lati del triangolo, si ha RA = CR e AP = PB cosicché i rapporti sopra diventano

che costituisce un risultato elementare ben noto e trattato: il baricentro divide le mediane in parti una doppia dell'altra.

Il teorema di Stewart

Una conseguenza dal carattere metrico che collega la lunghezza di un ceviano con le parti in cui viene suddiviso il lato di un triangolo è stabilita dal teorema che M. Stewart dimostrò nel 1746. In riferimento alla figura seguente

introduciamo le seguenti abbreviazioni per le lunghezze dei lati e degli altri segmenti coinvolti:

x e y sono perciò le lunghezze delle due parti nelle quali il lato BC viene suddiviso da AP. Allora il teorema suddetto stabilisce la validità della seguente relazione

La dimostrazione parte dall'applicazione del teorema di Carnot relativamente agli angoli supplementari BPA e APC. Pertanto

b2	=	y2 + t2 - 2y·t·cosAPC
c2	=	x2 + t2 - 2x·t·cosBPA

e poiché cosBPA = cos(180°-APC) = - cosAPC, le precedenti si riscrivono

b2	=	y2 + t2 - 2y·t·cosAPC
c2	=	x2 + t2 + 2x·t·cosAPC.

Moltiplicando la prima per x e la seconda per y ne discendono le

b2x	=	y2x + t2x - 2xy·t·cosAPC
c2y	=	x2y + t2y + 2xy·t·cosAPC.

Sommando in colonna le due espressioni si giunge alla

che si riscrive come

dalla quale, essendo x + y = a, abbiamo la tesi

Problema 1.3 Determinare la lunghezza delle mediane in termini delle lunghezze dei lati.
Soluzione

Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb.