| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. |
Partendo dalla definizione e da alcune conseguenti costruzioni della sezione aurea di un segmento, si individuano le connessioni con il pentagono e il decagono regolari in modo da giungere alle rispettive costruzioni. Successivamente si forniscono alcuni cenni al problema storico della costruzione dei poligoni regolari per poi trattare il pentadecagono e proporre infine la costruzione del poligono di 17 lati.
La sezione (o parte) aurea di un segmento è generalmente una nozione ben conosciuta e studiata. Si tratta di determinare un punto P di un segmento AB che lo divida in due parti, in modo che la maggiore sia media proporzionale fra l'intero segmento e la parte rimanente. Tradotto in termini di proporzioni dev'essere
| AB AP |
= | AP PB |
oppure
AP2 = AB x PB
Sia la definizione che caratterizza il punto P che quest'ultima relazione, suggeriscono di riprendere il teorema della secante e della tangente ad una circonferenza, dove appunto si sostiene una proprietà simile per il segmento di tangente avente per estremi il punto esterno e quello di contatto. Difatti è in base a questo teorema che possiamo costruire il punto P avente la proprietà delineata.
Si costruisca quindi una circonferenza tangente in B al segmento AB e avente il diametro pari ad AB (visualizzare gli elementi nascosti in fig. 1). Detto O il suo centro (2OB = AB) siano C e D le intersezioni della retta AO con la circonferenza tali che AC < AD. Riportato il segmento AC su AB per mezzo di una circonferenza di centro A e raggio AC, il punto P di intersezione di quest'ultima con AB soddisfa alla proprietà richiesta.
La dimostrazione segue dall'applicazione del teorema della secante e della tangente una volta che si identifichi AB come il segmento della tangente e AC e AD i segmenti della secante. L'applicazione comporta che sia
| AB2 | = | AC x AD |
ma essendo
| AD | = | AC + CD | = | AC + AB |
in quanto per costruzione è CD = 2OB = AB, si ha
| AB2 | = | AC x (AC + AB) |
o anche
| AB AC |
= | AC + AB AB |
Quest'ultima si può riscrivere come
| AB AC |
= | AC AB |
+ 1 | oppure | AB AC |
- 1 = | AC AB |
e quindi
| AB - AC AC |
= | AC AB |
Poiché AC = AP
AB - AC = AB - AP = PB
e l'ultima proporzione assume la forma
| PB AP |
= | AP AB |
che è equivalente alla proporzione data come definizione
| AB AP |
= | AP PB |
Volendo determinare in termini aritmetici la lunghezza di AP poniamo AB = a e AP = x. La definizione implica
| a x |
= | x a - x |
dalla quale deriva l'equazione
x2 + a x - a2 = 0
L'unica soluzione positiva che ammette tale equazione di II grado è
|
Notiamo che il reciproco di questo valore
| a x |
= |
è il famoso numero aureo (che indicheremo con φ), dotato di notevoli proprietà e collegato alla successione di Fibonacci (moltiplicato per -a fornisce pure la seconda soluzione dell'equazione sopra).
Concludiamo questa discussione sulla parte aurea di un segmento riportando la costruzione proposta da Euclide nella proposizione 11 del secondo libro degli Elementi.
Sia dato il segmento AB e sia C l'estremo del segmento AC perpendicolare ad AB e tale che AC = AB (fig. 2). M è il punto medio di AC. La circonferenza di centro M e raggio MB intersechi il prolungamento di CA dalla parte di A, in D. Infine l'ulteriore circonferenza con centro in A e raggio AD interseca internamente il segmento AB in P. Dimostriamo che AP è la sezione aurea di AB ossia soddisfa alla definizione oppure alla relazione
AP2 = AB x PB.
Per il teorema di Pitagora applicato a ![]() AMB risulta
AMB risulta
| AB2 | + | AM2 | = | MB2 |
da cui ricaviamo
| AB2 | = | MB2 | - | AM2 | = | MD2 | - | AM2 |
essendo MB = MD. Poiché P è interno ad AB possiamo scrivere
| AB x (AP + PB) | = | AB2 = MD2 - AM2 | |
| = | (MD + AM)·(MD - AM) = | CD x AD | |
| = | (AP + AB) x AP |
dove si sono considerate le congruenze AM = CM, AC = AB e AD = AP. Eseguendo le moltiplicazioni a primo e ultimo membro si ha
| AB x AP + AB x PB | = | AP2 + AB x AP | ossia | AB x PB | = | AP2 |
che è quanto si voleva dimostrare.
Le costruzioni di un triangolo equilatero e di un quadrato inscritti in un dato cerchio sono immediate e ben conosciute. Supponiamo pertanto di voler costruire un pentagono regolare considerando assegnato il raggio OA del cerchio ad esso circoscritto (fig. 3).
Sia quindi r = OA, l = AB la lunghezza (incognita) del lato del pentagono, d = AC = AD = CE la lunghezza delle sue diagonali, F il punto medio dell'arco CD ed estremo del diametro AF e infine, x = CF = FD. Applicando il teorema di Tolomeo rispettivamente ai quadrilateri ciclici ACDE e ACFD si ha
| AD · CE | = | CD · AE + AC · DE | AF · CD | = | CF · AD + AC · FD |
che, con le posizioni sopra, diventano
| d2 | = | l2 + dl | 2 r l | = | 2 x d. |
Dalla seconda deriva l'uguaglianza dei rapporti
| r x |
= | d l |
Detto t questo valore comune (t = r / x = d / l ) la prima relazione si può dividere per l2 e riscrivere
| d2 l2 |
= | 1 | + | d l |
cioè | t2 - t - 1 = 0 |
L'equazione in tal modo ottenuta fornisce la radice positiva (l'unica accettabile)
| t | = |
Dato che F divide in due parti congruenti l'arco CD e x è la lunghezza della corda CF, questa rappresenta pure la lunghezza del lato del decagono regolare. Il risultato ottenuto per t afferma quindi che il rapporto del raggio del cerchio con il lato del decagono regolare inscritto in esso è pari al numero aureo. Poiché il reciproco del numero aureo φ fornisce la sezione aurea dell'unità e 1 / φ = 1 / t = x / r, possiamo anche dire che il lato del decagono è la sezione aurea del raggio. Ma poiché siamo già in grado di costruire il segmento che sta in tale rapporto con uno dato, ciò significa che siamo pure in grado di costruire il decagono regolare e, di conseguenza, il pentagono regolare: per quest'ultimo sarà sufficiente unire alternativamente i vertici del decagono. Possiamo pertanto affermare che
Prima di procedere alla effettiva costruzione intendiamo ottenere questo risultato anche per altra via, utilizzando un metodo alternativo. Se consideriamo l'angolo al centro che insiste su un arco pari a 1/10 della lunghezza della circonferenza, quest'angolo possiede un ampiezza di 360°/10 = 36°. La corda sottesa da tale arco è evidentemente il lato del decagono regolare e la base del triangolo isoscele avente per lati obliqui due raggi. In figura 4 è rappresentato questo triangolo: poniamo x = AB, r = OA = OB mentre, dal fatto che ![]() AOB = 36°, discende
AOB = 36°, discende ![]() OAB =
OAB = ![]() OBA = 72°.
OBA = 72°.
Tracciata la bisettrice di ![]() OAB, questa incontra in C il lato OB. Poiché
OAB, questa incontra in C il lato OB. Poiché ![]() OAC = 36°,
OAC = 36°, ![]() OAC è isoscele con base in OA. Ne segue che AC = OC. Il
OAC è isoscele con base in OA. Ne segue che AC = OC. Il ![]() ABC possiede un angolo di 72° e un altro di 36° cosicché l'ampiezza del terzo dev'essere
ABC possiede un angolo di 72° e un altro di 36° cosicché l'ampiezza del terzo dev'essere ![]() ACB = 72°. Quindi anche
ACB = 72°. Quindi anche ![]() ABC è isoscele con AB = AC = OC. Inoltre quest'ultimo triangolo risulta simile a quello di partenza per il I criterio di similitudine,
ABC è isoscele con AB = AC = OC. Inoltre quest'ultimo triangolo risulta simile a quello di partenza per il I criterio di similitudine, ![]() ABC
ABC![]()
![]() OAB, per cui
OAB, per cui
| AB OA |
= | BC AB |
che con le posizioni poste, diventa
| x r |
= | r - x x |
dalla quale discende l'equazione
x2 + r x - r2 = 0
del tutto analoga a quella già vista precedentemente e che fornisce
| x r |
= | r x |
= |
Ciò conferma ancora una volta che la base AB di ![]() OAB è la parte aurea del lato obliquo cioè del raggio del cerchio circoscritto al decagono.
OAB è la parte aurea del lato obliquo cioè del raggio del cerchio circoscritto al decagono.
Sulla base di quanto detto possiamo ottenere facilmente la costruzione del decagono e del pentagono: per il primo è sufficiente dividere il raggio nella sua parte aurea e considerare quest'ultima come il lato del decagono.
figura 5
Tracciata pertanto la circonferenza avente per raggio il segmento OA, perpendicolare ad un secondo raggio OR (fig. 5), sia M il punto medio di OR. Costruita la circonferenza di centro M e raggio OM, questa incontra in S il segmento AM. Il segmento AS costituisce la sezione aurea del raggio e risulta congruente con il lato del decagono. È sufficiente ora riportarlo sulla circonferenza originaria con un'ulteriore circonferenza di centro A e raggio AS: le due intersezioni di questa forniscono due vertici, B e L, del decagono. Gli altri vertici si ottengono poi riportando ripetutamente il segmento AB lungo la circonferenza originaria (in fig. 5 le circonferenze necessarie a questo fine sono state nascoste). Il pentagono, ovviamente, si ottiene congiungendo alternativamente cinque dei 10 vertici del decagono.
Un approccio di tipo trigonometrico al problema della costruzione del poligono regolare inscritto in un cerchio ci fornisce un'ulteriore spunto per una costruzione alternativa del pentagono. Diamo innanzitutto una
Se quindi, consideriamo la perpendicolare condotta dal centro del cerchio al lato del poligono cioè l'apotema, il triangolo formato da questo lato e dai due raggi che lo collegano al centro risulta evidentemente isoscele (![]() OCD in figura 6, dove viene rappresentata la situazione con un pentagono). L'angolo al vertice di questo triangolo è pari a α = 360°/ n.
OCD in figura 6, dove viene rappresentata la situazione con un pentagono). L'angolo al vertice di questo triangolo è pari a α = 360°/ n.
Poiché
| CD | = | 2 HD | = | 2(OD sen |
||
| = |
|
da cui, posto OD = r,
| sn | = | 2r sen | 360° 2n |
= | 2r sen | 180° n |
Da questa discende facilmente che il lato del triangolo equilatero misura
| s3 | = | 2r sen 60° | = | r |
del quadrato
| s4 | = | 2r sen 45° | = | r |
dell'esagono
| s6 | = | 2r sen 30° | = | r, |
e del decagono
| s10 | = | 2r sen 18° | = | r | (1) |
dove in quest'ultima si è aggiunto, all'espressione goniometrica, il risultato trovato precedentemente. Lo scopo che ci proponiamo è di individuare un'espressione alternativa di s5 = 2r sen 36° ossia, in sostanza, di riscrivere sen 36°. Pertanto da (1) ricaviamo
| 2 sen 18° | = |
che, per l'identità goniometrica sen(α) = cos(90° - α) diventa
| 2 sen 18° | = | 2 cos (90° - 18°) | = | 2 cos 72° | = |
Otteniamo quindi che
| cos 72° | = | (2) |
Per mezzo della formula di bisezione
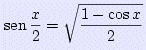
si può ora collegare il cos 72° con sen 36° e pertanto
| sen 36° | = |
Sostituendo in quest'ultima la (2) e tenuto presente che s5 = 2r sen 36° si ottiene in definitiva
| s5 | = r | 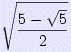 |
Evidentemente tale risultato appare difficilmente interpretabile se analizzato da solo mentre il suo significato emerge più evidente se lo colleghiamo a s6 e s10. Difatti è immediato verificare la validità dell'identità
| (s5)2 | = | (s6)2 | + | (s10)2 |
Poiché s6 rappresenta nient'altro che un segmento di lunghezza pari al raggio del cerchio mentre s10 la sua sezione aurea, si comprende come si possa costruire un segmento congruente con il lato s5 del pentagono: è sufficiente considerarlo come l'ipotenusa di un triangolo rettangolo i cui cateti siano il raggio del cerchio e la sua parte aurea. La seconda costruzione della sezione aurea di un segmento si mostra a tale proposito decisamente utile.
figura 7
Difatti in figura 7 il segmento OP è la sezione aurea del raggio OA e in tale costruzione rappresenta il lato del decagono s10. OA rappresenta invece il lato dell'esagono s6 per cui, applicando il teorema di Pitagora a ![]() OAP,
OAP,
| (s5)2 | = | AP2 | = | OA2 + OP2 | = | (s6)2 + (s10)2 |
È ora sufficiente riportare s5 sulla circonferenza originaria tramite una circonferenza di centro A e raggio AP per ottenere i due vertici, B ed E, adiacenti ad A del pentagono regolare inscritto. Al solito poi, si riporta tale distanza con ulteriori circonferenze (nascoste in fig. 7) per individuare i rimanenti due vertici.
Le precedenti costruzioni del pentagono coinvolgono in modo più o meno esplicito la sezione aurea di un segmento. In quella che qui presentiamo, proposta da Herbert W. Richmond nel 1893, si costruisce direttamente il cos 72° essendo, come sappiamo, 72° la misura dell'angolo al centro che sottende una corda pari al lato del pentagono.
figura 8
Costruita una circonferenza di raggio r = OA = OB con OA![]() OB (fig. 8), faremo coincidere con A uno dei vertici del pentagono. Allora, procedendo in verso antiorario, il secondo vertice A1, dovrà definire un angolo
OB (fig. 8), faremo coincidere con A uno dei vertici del pentagono. Allora, procedendo in verso antiorario, il secondo vertice A1, dovrà definire un angolo ![]() A1OA = 72° e la sua proiezione, C, sul raggio OA sarà pari a OC = r cos 72°.
A1OA = 72° e la sua proiezione, C, sul raggio OA sarà pari a OC = r cos 72°.
Sia quindi M il punto medio di OB e colleghiamo questo punto con A. Costruita la bisettrice di ![]() AMO questa incontri in C il raggio OA. Dimostriamo che OC = r cos 72° ossia che
AMO questa incontri in C il raggio OA. Dimostriamo che OC = r cos 72° ossia che
| OC | = | r cos 72° | = | r |
Poniamo ![]() CMO =
CMO = ![]() CMA = α e t = tg α. Allora, dalla definizione di tangente applicata al triangolo rettangolo
CMA = α e t = tg α. Allora, dalla definizione di tangente applicata al triangolo rettangolo ![]() OCM segue che
OCM segue che
| t | = | tg α | = | OC OM |
= | OC 1/2 OB |
= | 2 OC r |
mentre, applicando la medesima definizione a ![]() OAM, pure rettangolo,
OAM, pure rettangolo,
| tg 2α | = | OA OM |
= | 2 |
in quanto OM = 1/2 OA. Ricordando la formula di duplicazione della tangente
| tg 2θ | = | 2 tg θ 1 - tg2θ |
che lega tg 2θ con tg θ, e sostituendo quanto sopra, abbiamo
| 2 | = | 2 t 1 - t2 |
dalla quale, con qualche passaggio, abbiamo la nota equazione t2 + t - 1 = 0. Accettando il valore positivo in quanto 0< α < 90°, abbiamo
| t | = | 2 OC r |
= |
cioè
| OC | = | r |
come volevasi dimostrare. Tutto ciò suggerisce quindi di terminare la costruzione tracciando la perpendicolare per C ad OA cosicché i due punti di intersezione di questa con la circonferenza di centro O, A1 e A4 (fig. 8), devono formare un angolo di 72° con OA. A1 e A4 sono pertanto i due vertici del pentagono adiacenti ad A.
Si potrebbe pensare di procedere con costruzioni di poligoni aventi un numero di lati sempre maggiore ma sappiamo per i cenni che abbiamo dato al riguardo, che alcuni poligoni non possono essere costruiti solo con l'uso della riga e del compasso. Difatti Gauss e poi P. Wantzel hanno definitivamente dimostrato che si possono costruire solo i poligoni regolari il cui numero di lati sia un numero primo dispari del tipo Fm = 2p + 1, con p = 2m e m = 0, 1, 2... Questi numeri vengono detti primi di Fermat. Oggi, come ai tempi di Gauss, si conoscono solo cinque primi di Fermat (F5 = 4294967297 per esempio, è scomponibile in 641 x 6.700.417 ma da Fermat era ritenuto, erroneamente, un numero primo)
| m | 0 | 1 | 2 | 3 | 4 |
| Fm | 3 | 5 | 17 | 257 | 65537 |
Considerando che dal poligono regolare di n lati si può ottenere il poligono regolare di 2n lati con la semplice divisione dell'arco sotteso dal lato del poligono in due archi congruenti, partendo dal triangolo equilatero possiamo ritenere costruibili i poligoni
| 3, | 6, | 12, | 24, | 48, | ..., | 3·2n, |
| 4, | 8, | 16, | 32, | 64, | ..., | 2n, |
| 5, | 10, | 20, | 40, | 80, | ..., | 5·2n, |
| 15, | 30, | 60, | 120, | 240, | ..., | 3·5·2n, |
| 17, | 34, | 68, | 136, | 272, | ..., | 17·2n, |
| ..., | ..., | ..., |
Tra quelli con il minor numero di lati, diamo qualche cenno sul pentadecagono (15 lati) e successivamente, forniamo senza dimostrazione, la costruzione del poligono di 17 lati (eptadecagono).
Poiché siamo in grado di costruire un triangolo equilatero e un pentagono regolare, ne segue che possiamo costruire un angolo di 60° e di 36°. Ma valendo l'identità
| 60° - 36° = 24° | = | 360° 15 |
si intuisce la costruzione necessaria per ottenere un tale poligono: si dovrà costruire l'angolo di 24° come differenza di uno di 60° con un altro 36°. La figura 9 mostra come si possa facilmente ottenere ciò.
figura 9
Costruiti il triangolo equilatero ![]() ABC e il pentagono ADEFG in modo da condividere il medesimo vertice A e simmetricamente rispetto al diametro per A, siano H il punto medio di BC e K il punto medio di EF: OH e OK sono quindi rispettivamente le apoteme ai lati BC e EF. Poiché
ABC e il pentagono ADEFG in modo da condividere il medesimo vertice A e simmetricamente rispetto al diametro per A, siano H il punto medio di BC e K il punto medio di EF: OH e OK sono quindi rispettivamente le apoteme ai lati BC e EF. Poiché ![]() BOH = 60° e
BOH = 60° e
| = | 2 |
= | 1 2 |
· | 360° 5 |
= | 36° |
ne segue che
| = |
= | 60° - 36° | = | 24° |
cosicché i punti B ed E sono gli estremi di un segmento congruente al lato del pentadecagono.
In alternativa si può notare che nell'arco ADB, a partire da A, dovranno essere contenuti esattamente 15 / 3 = 5 lati del pentadecagono mentre nell'arco minore AD ve ne dovranno stare esattamente 15 / 5 = 3. Se ne deduce che nell'arco minore DB sono contenuti esattamente due lati del pentadecagono cosicché è sufficiente suddividere quest'arco in due parti congruenti per disporre di tre vertici consecutivi del pentadecagono e risolvere nuovamente il problema della sua costruzione.
La costruzione del poligono regolare di 17 lati che segue è stata proposta, assieme a quella già esposta del pentagono, da Herbert W. Richmond e risulta più breve di quella originariamente data da Gauss. I vertici saranno individuati dalle lettere A, A1, A2,....A16 ed evidentemente sarà sufficiente individuare due vertici adiacenti per determinare il lato dell'eptadecagono. La costruzione è rappresentata in figura 10 e i passi necessari risultano i seguenti:
figura 10
Il segmento A3A4 = A4A5 = s17 rappresenta il lato cercato dell'eptadecagono. Gli altri vertici discendono facilmente riportandoli con circonferenze di raggio A3A4 (fig. 11).
figura 11
| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. |
|
|||||||||||