Appendice 1
Alcuni utili teoremi di geometria elementare e di trigonometria
- Teorema
- Il punto medio di un segmento è unico.
- Teorema
- L'asse di un segmento è il luogo geometrico dei
punti equidistanti dagli estremi del segmento.
- Teorema
- Gli angoli opposti al vertice sono congruenti.
- Teorema
- La bisettrice di un angolo è il luogo geometrico dei punti del piano equidistanti dai lati dell'angolo.
- Teorema
- Gli assi dei lati di un triangolo si incontrano in uno stesso punto detto circocentro.
- Teorema
- Le bisettrici degli angoli interni di un triangolo si incontrano in uno stesso punto detto incentro.
- Teorema
- Le altezze di un triangolo si intersecano in uno stesso punto detto ortocentro.
- Teorema
- Le mediane di un triangolo si incontrano in uno stesso punto (detto baricentro) che divide ciascuna di esse in due parti delle quali una, e cioè quella avente come altro estremo il vertice, è congruente con il doppio dell'altra parte.
- Primo criterio di congruenza dei triangoli (LAL)
- Se due triangoli hanno ordinatamente congruenti un angolo e la coppia di lati che lo comprendono, allora i triangoli sono congruenti.
- Secondo criterio di congruenza dei triangoli (ALA)
- Se due triangoli hanno ordinatamente congruenti un lato e gli angoli che lo comprendono, allora i due triangoli sono congruenti.
- Terzo criterio di congruenza dei triangoli (LLL)
- Se due triangoli hanno ordinatamente congruenti i tre lati, allora tali triangoli sono congruenti.
- Teorema di Talete
- Un fascio di rette parallele determina su due trasversali due classi di segmenti direttamente proporzionali (e viceversa).
- Primo criterio di similitudine dei triangoli
- Se due triangoli hanno due coppie di angoli corrispondenti congruenti, essi sono simili.
- Secondo criterio di similitudine dei triangoli
- Se due triangoli hanno una coppia di angoli corrispondenti congruenti tra lati omologhi in proporzione, essi sono simili.
- Terzo criterio di similitudine dei triangoli
- Se due triangoli hanno tutti i lati omologhi in proporzione, essi sono simili.
- Teorema di Pitagora
- In un triangolo rettangolo il quadrato costruito sull'ipotenusa è equivalente alla somma dei quadrati costruiti sui cateti.
- Teorema sul triangolo isoscele
- Condizione necessaria e sufficiente affinché un triangolo sia isoscele è che la mediana e l'altezza ad un lato, coincidano.
- Teorema sui punti medi di due lati
- Il segmento che ha per estremi i punti medi di due lati di un triangolo è parallelo al terzo e la sua lunghezza è la metà del terzo.
- Teorema
- Le bisettrici degli angoli formati da due rette secanti sono perpendicolari.
- Teorema
- Condizione necessaria e sufficiente affinché un quadrilatero convesso sia un parallelogramma è che i suoi angoli opposti siano congruenti.
- Teorema
- Condizione necessaria e sufficiente affinché un quadrilatero convesso sia un parallelogramma è che i lati opposti siano congruenti.
- Teorema
- Condizione necessaria e sufficiente affinché un quadrilatero convesso sia un parallelogramma è che gli angoli aventi un lato in comune siano supplementari.
- Teorema
- Condizione necessaria e sufficiente affinché un quadrilatero convesso sia un parallelogramma è che abbia una coppia di lati opposti paralleli e congruenti.
- Teorema.
- Condizione necessaria e sufficiente affinché un quadrilatero convesso sia un parallelogramma è che le diagonali si bisechino vicendevolmente.
- Teorema
- Un quadrilatero convesso è inscritto in una circonferenza se e solo se i suoi angoli interni opposti sono supplementari.
- Teorema
- Per tre punti non allineati passa una ed una sola circonferenza.
- Teorema dei seni
- In un triangolo qualsiasi di lati a, b, c, angoli
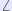 A,
A, 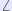 B,
B, 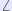 C e raggio della circonferenza circoscritta R, sono costanti i rapporti
C e raggio della circonferenza circoscritta R, sono costanti i rapporti
a
sen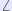 A A |
= |
b
sen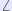 B B |
= |
c
sen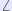 C C |
= |
2R |
- Teorema di Carnot (o del coseno)
- In un triangolo qualsiasi, il quadrato della misura di un lato è uguale alla somma dei quadrati delle misure degli altri due diminuita del doppio prodotto di queste due per il coseno dell'angolo opposto al primo.
| a2 |
= |
b2 + c2 - 2 b c cos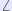 A A |
|
b2 |
= |
a2 + c2 - 2 a c cos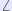 B B |
|
c2 |
= |
a2 + b2 - 2 a b cos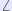 C C |
- Teorema
- In ogni triangolo la differenza dei quadrati costruiti su due lati è equivalente al doppio dell'area del rettangolo avente per lati, il terzo lato del triangolo (c) e la proiezione sulla retta di quest'ultimo della mediana relativa ad esso (mc).
- Teorema sulle retta parallelle
- Due rette sono parallele se e solo se formano con una trasversale una coppia di angoli alterni interni (oppure alterni esterni, oppure corrispondenti) congruenti.
- Teorema
- In circonferenze congruenti o nella stessa circonferenza, ad archi congruenti corrispondono angoli al centro congruenti.
- Teorema
In circonferenze congruenti o nella stessa circonferenza, a corde congruenti corrispondono archi congruenti.
- Teorema
- In circonferenze congruenti o nella medesima circonferenza, angoli alla circonferenza che insistono su archi congruenti sono congruenti e, viceversa, angoli alla circonferenza congruenti insistono su archi congruenti.
- Teorema
- Due secanti parallele ad una circonferenza intercettano su di essa archi uguali e viceversa.
- Teorema
- Ogni angolo alla circonferenza è congruente con la metà dell'angolo al centro che insiste sullo stesso arco.
- Teorema
- Un angolo esterno di un triangolo è congruente con la somma degli angoli interni non adiacenti ad esso.
- Teorema
- La somma degli angoli interni di un triangolo è congruente ad un angolo piatto.
- Teorema
- La somma degli angoli interni di un poligono convesso è congruente con (n-2)180° dove n rappresenta il numero dei lati del poligono.
- Teorema
- In un triangolo isoscele, la mediana avente origine nel vertice è bisettrice dell'angolo al vertice ed è perpendicolare alla base.
- Area di un triangolo
- Se a, b, c sono le lunghezze dei lati di un triangolo e α, β, γ i corrispondenti angoli, l'area del triangolo è espressa da
| Area |
= |
1
2 |
a b sen γ |
= |
1
2 |
a c sen β |
= |
1
2 |
b c sen α |
- Teorema della bisettrice.
- La bisettrice di un angolo interno di un triangolo divide il lato opposto all'angolo in parti proporzionali agli altri due lati e viceversa.
- Teorema della bisettrice dell'angolo esterno
- La bisettrice di un angolo esterno di un triangolo interseca il prolungamento del lato opposto in un punto le cui distanze dagli estremi di questo lato sono proporzionali agli altri due lati.
- Teorema.
- I segmenti delle rette tangenti ad una circonferenza condotte da un punto P esterno ad essa, aventi un estremo in P e l'altro in uno dei punti di contatto, sono congruenti.
- Teorema.
- Qualsiasi figura geometrica è congruente con tutte quelle che si ottengono da essa per simmetria centrale.