Esperienze di Fisica
Questa pagina tratta dell'allestimento e dell'elaborazione di un'esperienza svolta in un laboratorio didattico riguardante il moto oscillatorio smorzato di un corpo rigido. Per una introduzione teorica si veda la pagina precedente.
- Schema dell'esperienza e allestimento
- Rappresentazione delle misure
- Riduzione dei modelli e analisi numerica
- Osservazioni ed esiti
- Dipendenza dell'ampiezza dal tempo
- Bibliografia
- Materiali didattici e persone
Schema dell'esperienza e allestimento
Lo schema seguito per predisporre l'esperienza è riassunto in figura 1 e vede come elemento principale per l'acquisizione dei dati angolari il sensore di moto rotatorio. L'asse di rotazione del corpo rigido è direttamente collegato alla puleggia del sensore che, tramite un'interfaccia, invia i dati al PC dove è installato un software per la raccolta e interpretazione delle misure. Tale software permette pure l'esportazione dei dati in un formato leggibile da un foglio di calcolo.
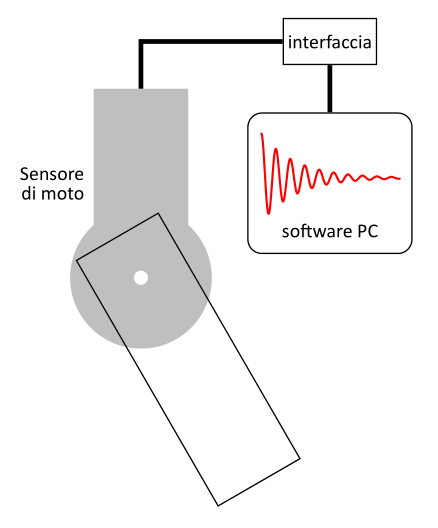
Nell'allestimento scelto, il corpo oscillante è costituito da una piccola barretta di alluminio (un righello di un decimetro) libera di ruotare in prossimità di un suo estremo e, come detto, con asse collegato direttamente al sensore di moto (figure 2 e 3).

|

|
|
|
Figura 2.
|
Figura 3.
|
Avviata da PC l'acquisizione dei dati, la barretta viene spostata dalla verticale fino ad una ampiezza scelta di volta in volta e quindi lasciata libera. La forza di attrito viscoso si ottiene sia immergendo parzialmente in acqua l'estremo inferiore della barretta (fig. 4) ma pure facendo scorrere l'altro estremo della barretta davanti ad un forte magnete (recuperato da un vecchio hard disk, figure 5 e 6): in tal modo si generano nella parte metallica del corpo oscillante delle correnti di Foucault la cui intensità è legata alla velocità del moto.


|

|
|
|
Figura 5.
|
Figura 6.
|
L'attrito radente viene invece generato ponendo a contatto la parte della barretta più vicina all'asse di rotazione con un pennello in modo che le setole "accompagnino" in qualche modo il corpo oscillante (figure 7 e 8).

|

|
|
|
Figura 7.
|
Figura 8.
|
In ogni caso le misure grezze fornite dal sensore riguardano l'elongazione rispetto alla posizione di equilibrio verticale e i corrispondenti istanti di tempo.
Rappresentazione delle misure
Per come si è avviata la registrazione, le coppie (tempo, elongazione), (\(t,\theta)\), rilevate nella fase di spostamento della barretta dalla verticale vanno escluse per cui, dopo aver importati tali dati in un foglio di calcolo,
è necessaria una loro rappresentazione grafica per riconoscere l'istante del rilascio. Eliminati tali coppie, conviene eseguire una traslazione dei tempi così da assegnare al primo dato utile l'istante zero. Similmente vanno
esclusi pure tutti quei dati che mostrano alla fine del moto la barretta oramai in quiete e verticale.
Di seguito riportiamo gli andamenti di
- due prove soggette ad attrito viscoso (figure 9 e 10) e di altre
- due con attrito radente (figure 11 e 12)
e, come si può evincere osservando il foglio di calcolo associato, abbiamo scelto di interrompere l'elaborazione quando l'ampiezza massima di oscillazione è scesa al di sotto di 0,02 rad (poco più di 1 grado) che, a nostro parere, sembra pure essere la risoluzione angolare del sensore di moto.
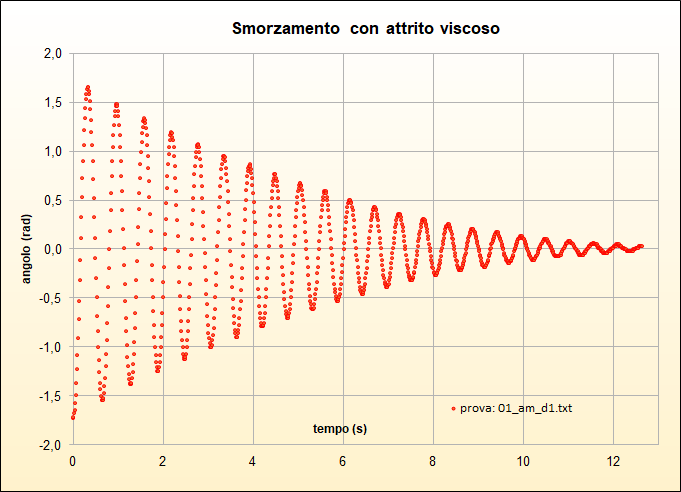
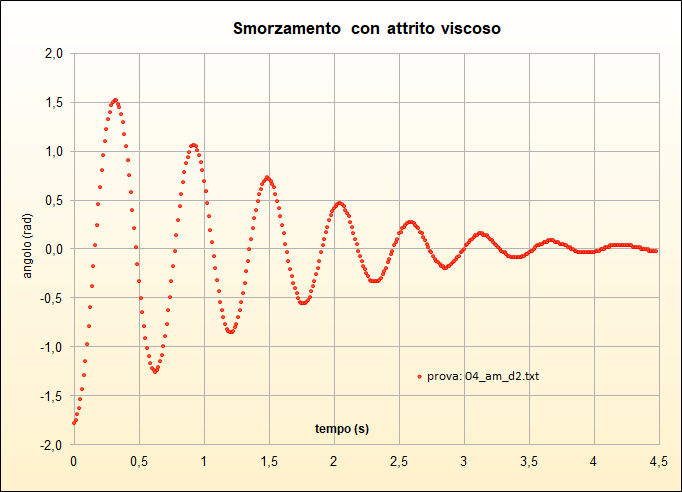
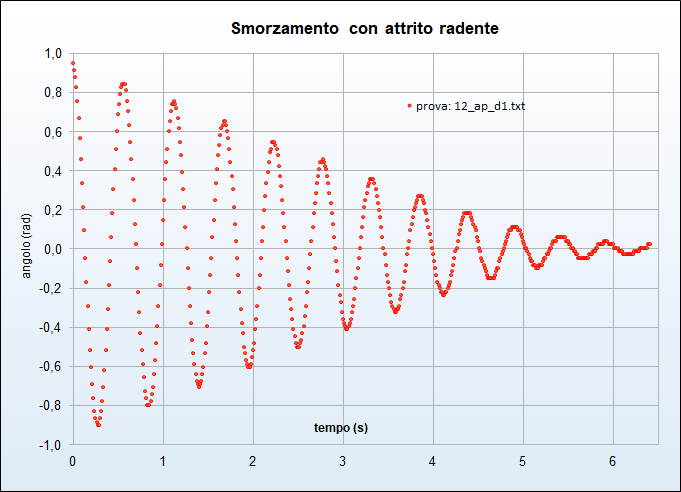
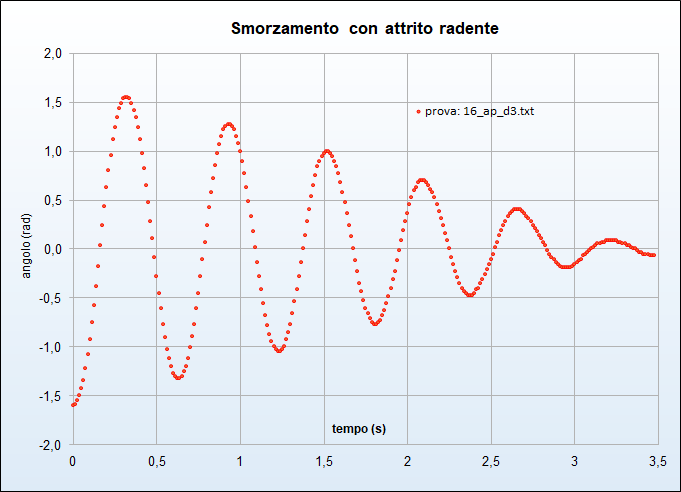
Come si può osservare dalla scala verticale delle precedenti immagini, l'elongazione assume valori ben maggiori del tipico dominio delle piccole oscillazioni \([0^\circ,10^\circ]\) e ciò dà ragione del fatto che, diversamente da quanto si fa in tale contesti, non abbiamo approssimata la funzione \(\sin\theta\) presente nelle equazioni del moto all'angolo \(\theta\). Pertanto i modelli seguenti non sono limitati alle piccole oscillazioni.
Riduzione dei modelli e analisi numerica
Per riprodurre gli andamenti rilevati e verificare l'adeguatezza dei modelli ai dati sperimentali seguiremo un metodo numerico di risoluzione dei sistemi di equazioni differenziali ordinarie (ODE) in particolare il metodo di Eulero che,
diversamente da approcci analitici peraltro non facili
nel caso di ampiezze di oscillazione qualsiasi, permette comunque una soddisfacente comprensione di tali sistemi ma a partire da relazioni relativamente più semplici.
Nel caso di moto soggetto ad attrito viscoso le relazioni che descrivono la velocità angolare e l'accelerazione angolare (definita pure come \(d\omega/dt\)), sono le seguenti (si veda la pagina precedente)
\begin{equation}
\cases{\displaystyle\omega=\frac{d\theta}{dt}\cr\\[-5pt] \displaystyle\alpha=\frac{d\omega}{dt}=-\frac{g}{l_{eff}}\sin\theta- b\,\omega. \cr}
\end{equation}
Se ora supponiamo che in un intervallo \(\Delta t=t_{j+1}-t_j\) con \(j=0,\,1,\dots,N\) relativamente piccolo sia l'accelerazione angolare \(\alpha\) che la velocità angolare siano costanti, possiamo in tale intervallo ritenere che
le variazioni \(\Delta\theta\) e \(\Delta\omega\), rispettivamente dell'angolo \(\theta\) e della velocità angolare, siano proporzionali all'intervallo stesso \(\Delta t\), e quindi scrivere
\begin{equation}
\cases{\Delta \theta=\omega\Delta t\cr \\[-5pt] \displaystyle\Delta\omega =\alpha\Delta t=\biggl(-\frac{g}{l_{eff}}\sin\theta- b\,\omega\biggr)\Delta t.\cr}
\end{equation}
Esplicitiamo ora le variazioni nel \(j\)-esimo intervallo come
\begin{equation}
\Delta\omega=\omega_{j+1}-\omega_j,\qquad \Delta\theta=\theta_{j+1}-\theta_j,\qquad \omega=\omega_j,\qquad \theta=\theta_j
\end{equation}
cosicché la precedente diviene
\begin{equation}
\cases{\theta_{j+1}-\theta_j =\omega_j\Delta t\cr\\[-5pt] \displaystyle\omega_{j+1}-\omega_j =\biggl(-\frac{g}{l_{eff}}\sin\theta_j- b\,\omega_j\biggr)\Delta t \cr}
\end{equation}
dalla quale discende
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]
{\cases{t_{j+1}=t_j+\Delta t\cr \\[-5pt] \theta_{j+1}=\theta_j +\omega_j\Delta t\cr \\[-5pt] \displaystyle\omega_{j+1}=\omega_j +\biggl(-\frac{g}{l_{eff}}\sin\theta_j- b\,\omega_j\biggr)\Delta t \qquad\hbox{con}\qquad j=0,\,1,\dots,N\cr}}
\end{equation}
sistema che mostra come le grandezze angolari varino con legge lineare nell'intervallo \(\Delta t\).
Nel caso dell'attrito radente si procede allo stesso modo sostituendo comunque l'accelerazione angolare \(-(g/l_{eff})\sin\theta_j- b\,\omega_j\) con il termine \(-(g/l_{eff})\sin\theta_j- c\,\textrm{sgn}(\omega_j)\) e quindi
\begin{equation}\bbox[border:1px solid red,15px,#ffffcc] {\cases{t_{j+1}=t_j+\Delta t\cr \\[-5pt] \theta_{j+1}=\theta_j +\omega_j\Delta t\cr \\[-5pt] \displaystyle\omega_{j+1}=\omega_j +\biggl(-\frac{g}{l_{eff}}\sin\theta_j- c\,\textrm{sgn}(\omega_j)\biggr)\Delta t \qquad\hbox{con}\qquad j=0,\,1,\dots,N.\cr}} \end{equation}Sulla base di tali relazioni possiamo impostare la simulazione numerica e quindi, gradualmente adeguarla agli andamenti rilevati: le fasi, rappresentate in figura 13, sono quindi
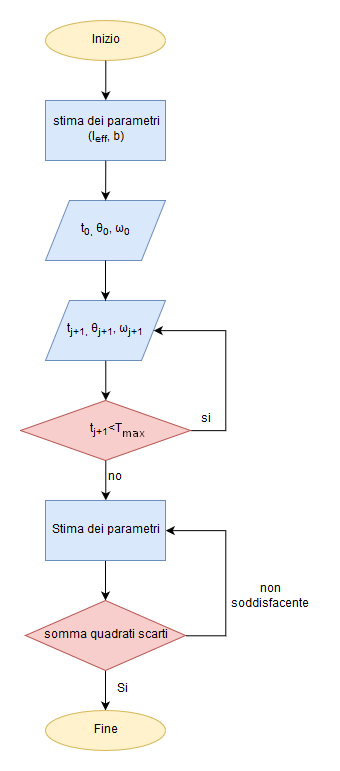
- una prima stima dei parametri \(l_{eff}\) e di \(b\) (oppure \(c\) per l'attrito radente).
Se per \(l_{eff}\) si può iniziare dal valore teorico espresso dalla \(l_{eff}=(h^2+L^2/12)/h\) e riportato nella prima parte (dedotto, nella nostra esperienza, da \(h=46\) mm e \(L=108\) mm), per i coefficienti d'attrito \(b\) e \(c\) è necessario procedere per tentativi in quanto legati a fattori difficilmente valutabili (attrito puleggia, attriti della parte immersa e variabile nelle diverse prove, correnti parassite,...); - inserimento dei valori iniziali di \(t_0\), \(\theta_0\) e \(\omega_0\) (in verde in fig. 14);

- calcolo dell'accelerazione angolare \(-(g/l_{eff})\sin\theta_0- b\,\omega_0\) (oppure \(-(g/l_{eff})\sin\theta_0- c\,\textrm{sgn}(\omega_0)\)) (in rosa in fig. 15);

- calcolo dei valori di fine intervallo di \(t_{j+1},\, \omega_{j+1},\, \theta_{j+1},\) (in celeste in fig. 16) e

- copia delle corrispondenti formule nelle celle sottostanti fino all'istante finale della rilevazione.
- Segue quindi un affinamento della stima dei parametri \(l_{eff}\) e di \(b\) (oppure \(c\)) e orientata alla minimizzazione della somma dei quadrati degli scarti tra misura e simulazione, \(\sum(\theta_{sper}-\theta_{sim})^2=\sum\Delta\theta^2\) e accompagnata da un confronto dei rispettivi andamenti grafici.
Osservazioni ed esiti
Di seguito riportiamo gli esiti numerici e grafici di quattro prove:
- due con smorzamento soggetto ad attrito viscoso:
- due caratterizzate da un prevalente attrito radente,
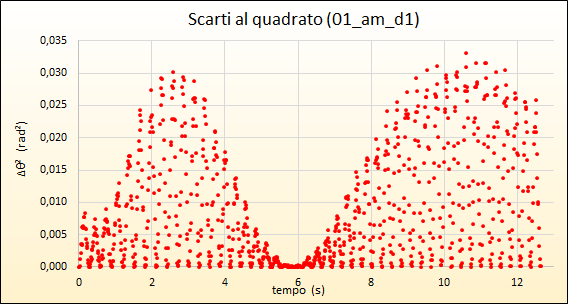
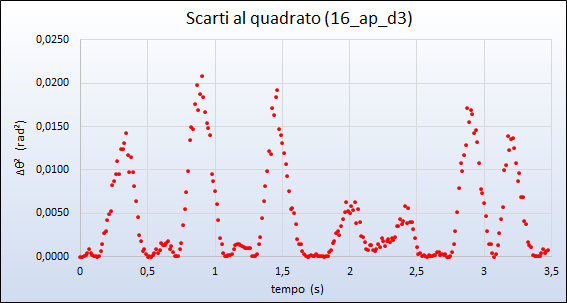
Quale supporto visivo utile per ricercare le condizioni di massimo accordo tra la simulazione numerica e i dati sperimentali associamo pure il grafico dei quadrati degli scarti in funzione del tempo:
in tal modo appaiono evidenti le regioni di minimo e massimo accordo e come queste, nel foglio di calcolo, si modifichino al variare dei due parametri liberi.
Prima prova: attrito viscoso
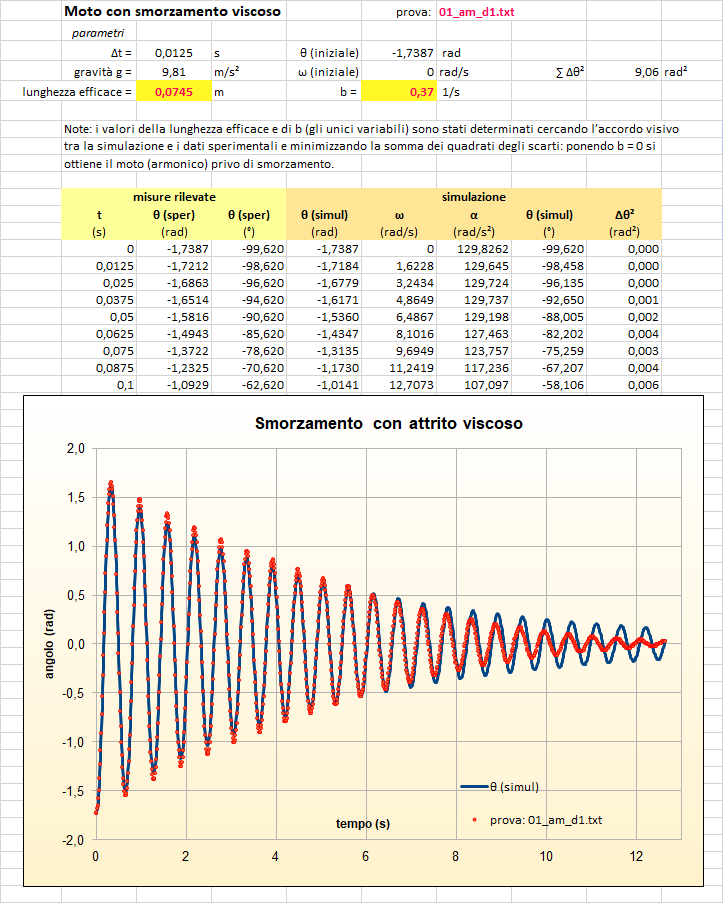
Seconda prova: attrito viscoso
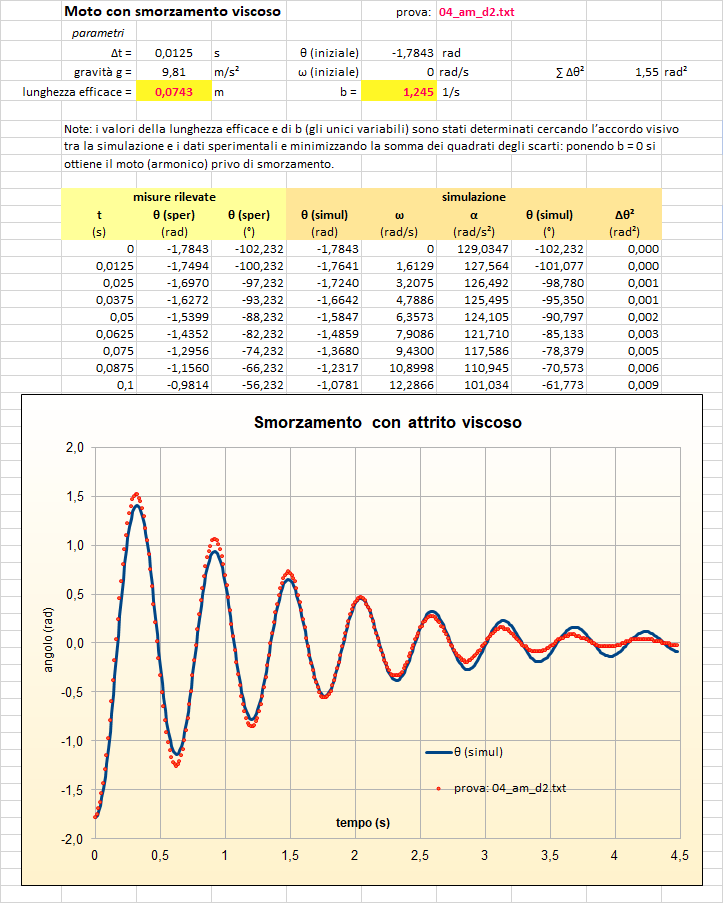
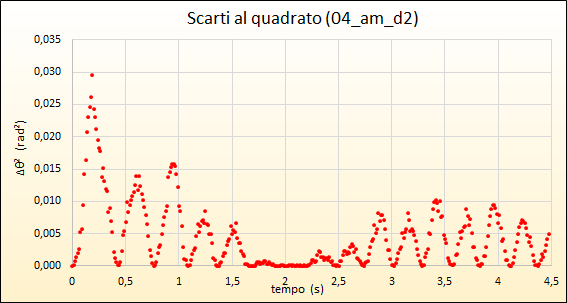
Il confronto grafico tra l'andamento sperimentale e quello numerico mostra un sostanziale accordo mentre qualche differenza emerge nella fase finale del moto quando il modello sembra sottostimare l'attrito viscoso mostrando, la simulazione, un'ampiezza maggiore di quella rilevata.
Nel caso di attrito radente il confronto appare complessivamente più soddisfacente, esito confermato pure da una minore dispersione dei quadrati degli scarti.
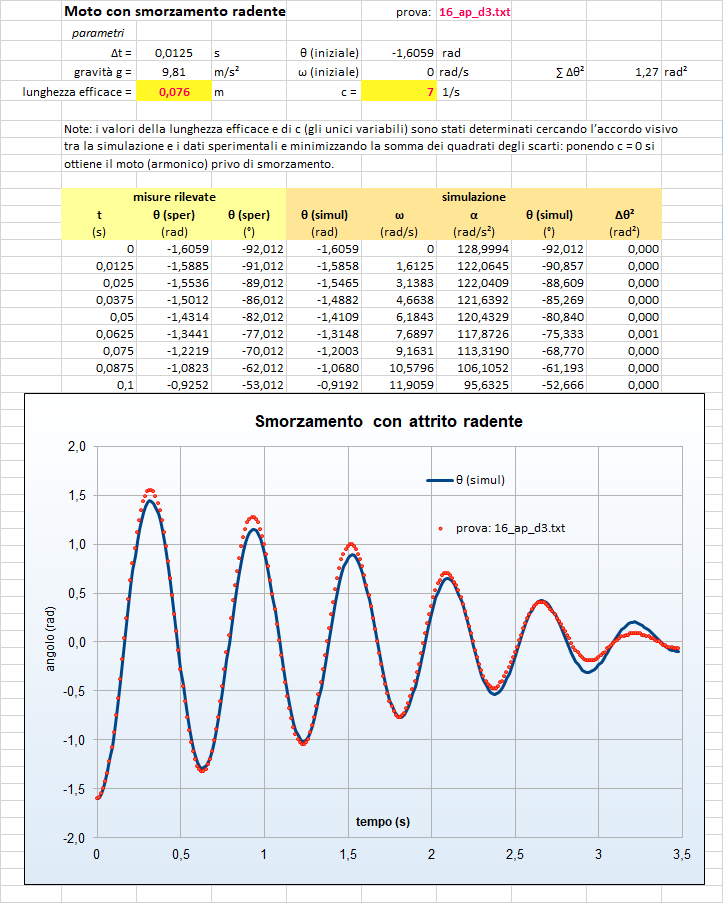
Terza prova: attrito radente
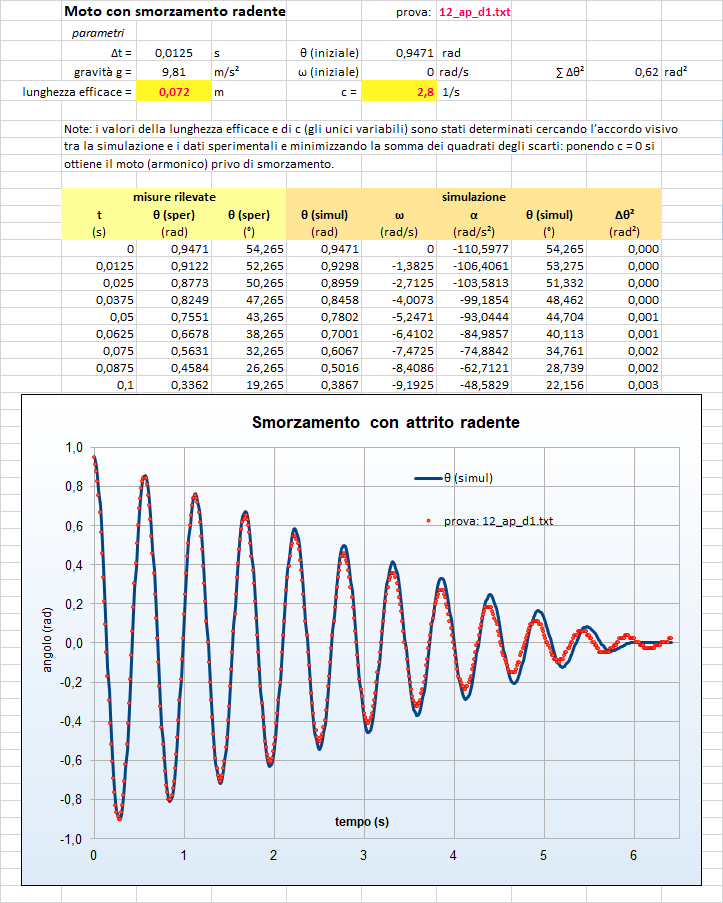
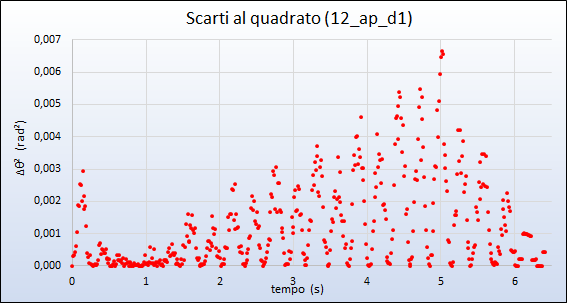
Quarta prova: attrito radente
Dipendenza dell'ampiezza dal tempo
In tutte le prove evidentemente l'ampiezza decresce al variare di \(t\) per cui la legge che emerge è del tipo
\begin{equation}\theta(t)=A(t)\sin(\omega t+\phi) \end{equation}con la funzione \(A(t)\) monotòna decrescente ma, con altrettanta evidenza,
- nel caso dell'attrito viscoso \(A(t)\) segue una legge di decrescita esponenziale cioè del tipo \begin{equation}A(t)=a e^{-\beta t} \end{equation} peraltro aspettata dato che la soluzione dell'equazione differenziale nel caso delle piccole oscillazioni conduce proprio a tale andamento;
- nel caso di attrito radente la legge di decrescita è di tipo lineare e quindi formalmente rappresentata dalla \begin{equation}A(t) =(-\alpha t+ \gamma). \end{equation} dove il parametro \(\alpha\) non va confuso con l'accelerazione angolare trattata precedentemente.
Intendiamo quindi integrare la nostra indagine determinando i parametri che caratterizzano i due andamenti dell'ampiezza così da rappresentare la corrispondente funzione assieme ai dati rilevati.
Per determinare tali parametri seguiamo un metodo elementare ossia imponiamo il passaggio della curva rappresentativa di \(A(t)\) per due punti scelti tra i dati sperimentali. Un metodo più elaborato è invece proposto nel
notebook di Mathematica associato a questo lavoro e distribuito al termine di questa pagina.
Pertanto se la curva descritta dalla \(A(t)=ae^{-\beta t}\) deve passare per i punti
\((t_1,\theta_1)\)
e \((t_2,\theta_2)\), allora i parametri \(\beta\) e \(a\) si calcolano nell'ordine con le relazioni (la loro deduzione è elementare)
Analogamente, per l'andamento lineare si ha
\begin{equation} \alpha=-\frac{\theta_2-\theta_1}{t_2-t_1},\qquad \gamma=\frac{t_2\theta_1-t_1\theta_2}{t_2-t_1}. \end{equation}Nelle riquadro delle figure sottostanti (figg. 25, 26, 27, 28) si riportano le coppie di punti \((t_1,\theta_1)\) e \((t_2,\theta_2)\) scelte tra i massimi in corrispondenza delle quali il fattore sinusoidale vale 1: è con tali coppie che si sono ottenuti i valori dei parametri riportati nel riquadro.
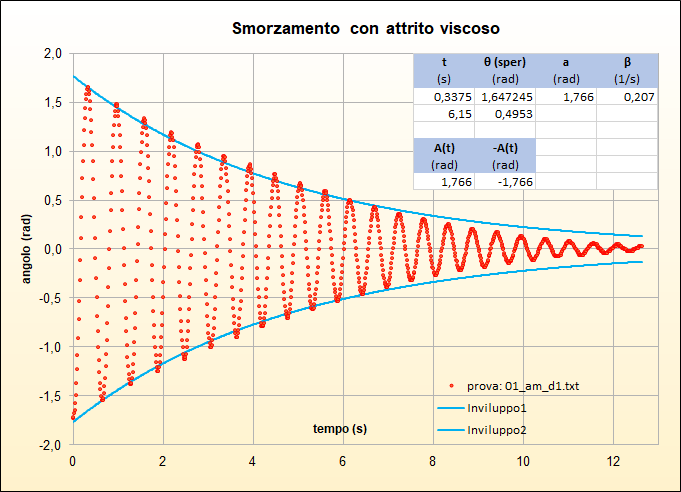
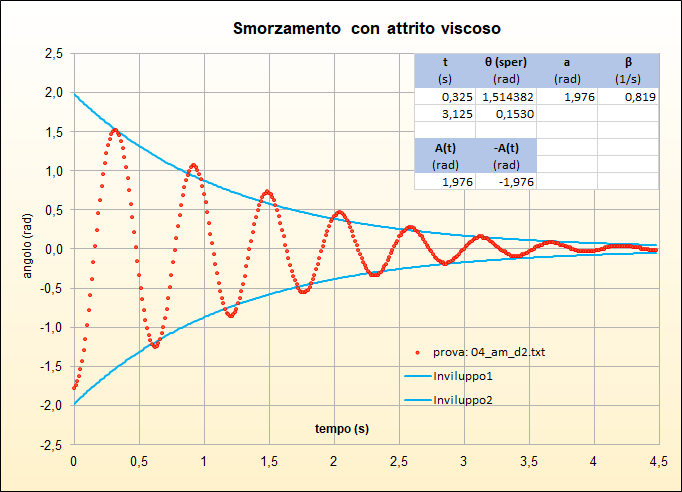
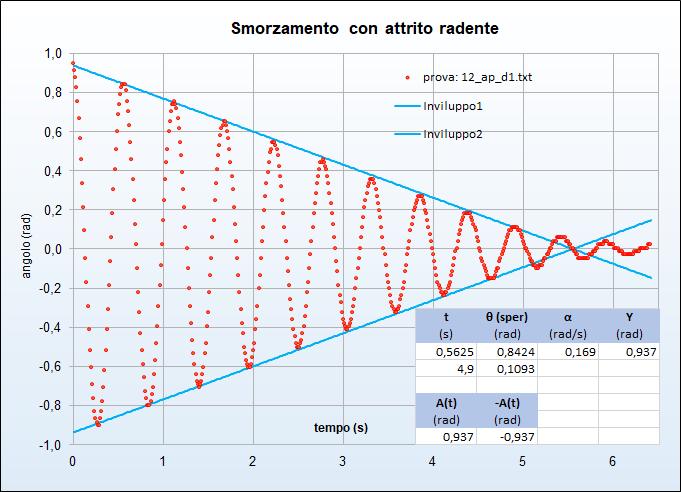
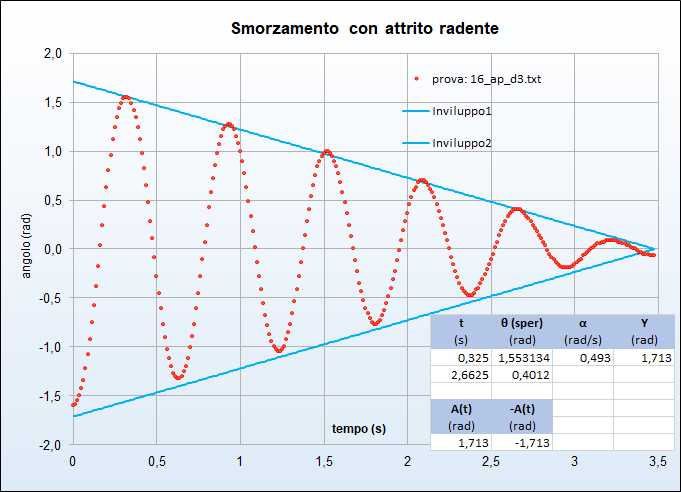
Seppur individuate con un metodo elementare, le funzioni descrivono abbastanza bene la decrescita dell'ampiezza e permettono una discreta distinzione tra i due tipi di attrito e il loro diverso carattere.
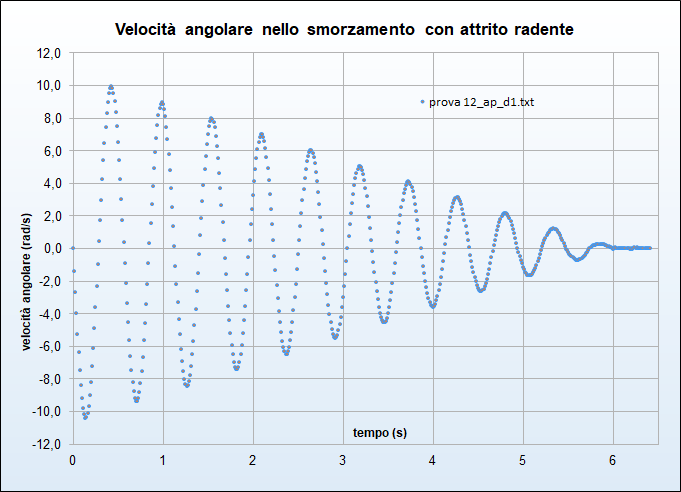
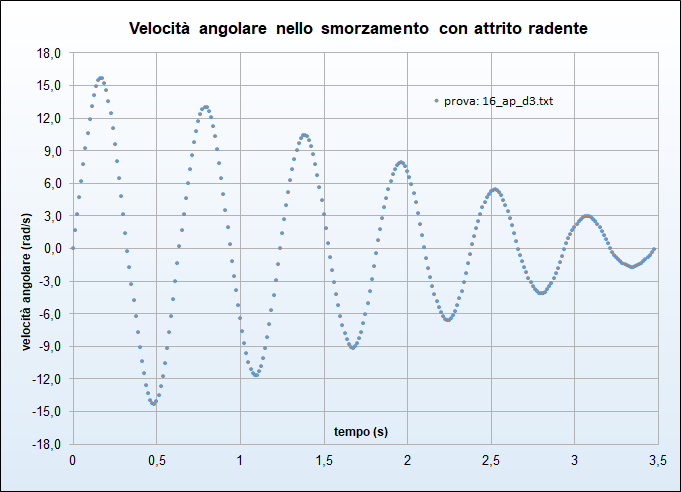
Concludiamo la nostra indagine riportando i grafici della velocità angolare \(\omega_j\) in funzione del tempo per le quattro prove discusse (figg. 29, 30, 31, 32): in analogia al moto armonico possiamo osservare tramite un confronto con i corrispondenti grafici (e, analiticamente, sul foglio di calcolo) come il valore assoluto dei massimi di tale grandezza siano raggiunti quando l'elongazione è nulla ossia il corpo passa per la verticale: viceversa la velocità è nulla quando l'elongazione è, in valore assoluto, massima. Osserviamo inoltre, come la diminuzione dell'ampiezza in funzione del tempo permetta, ancora, di distinguire le due forme di attrito.
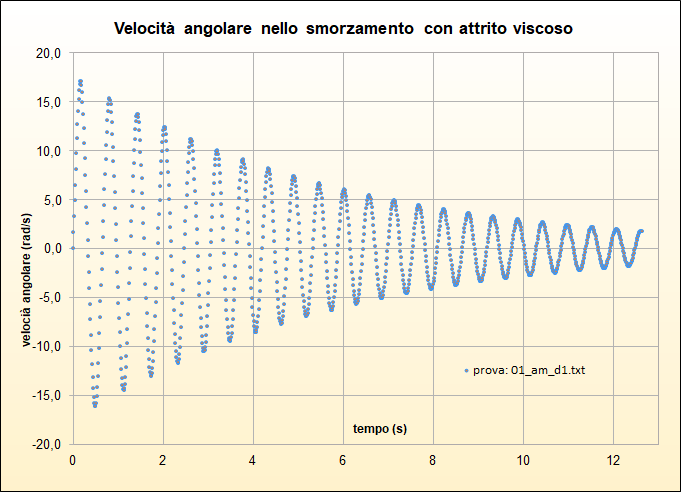
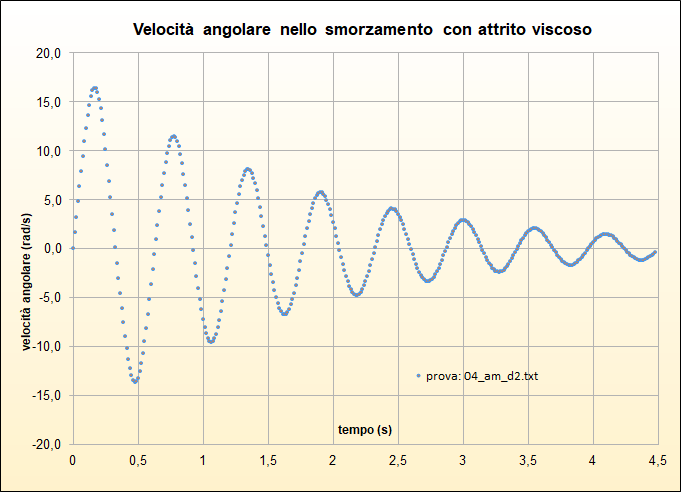
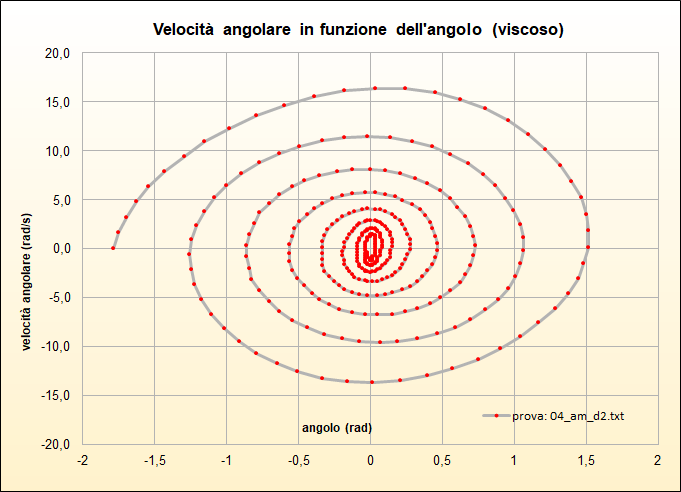
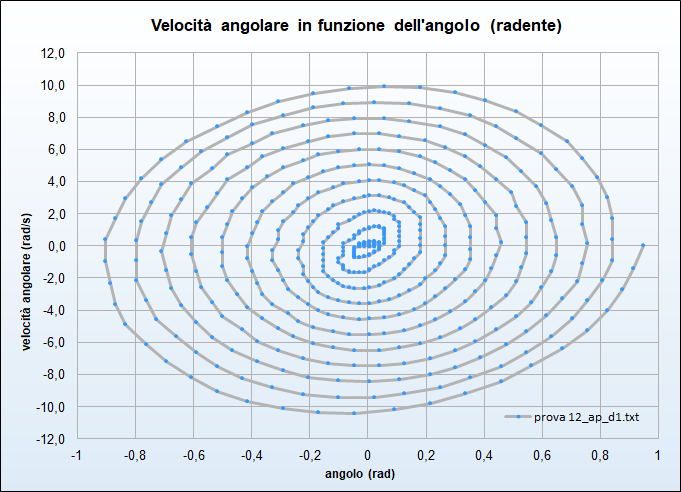
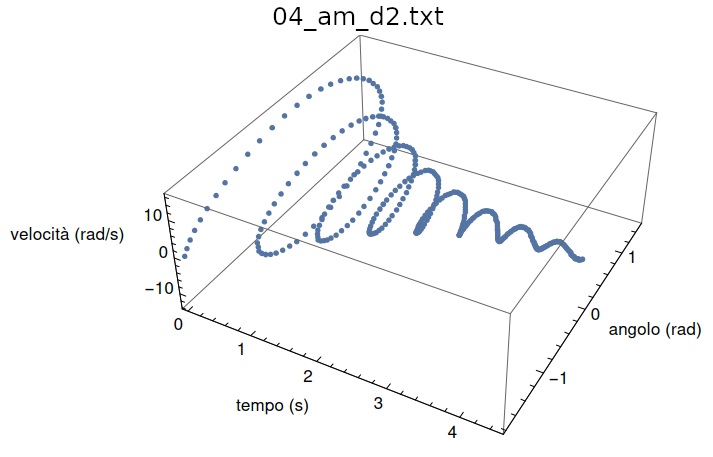
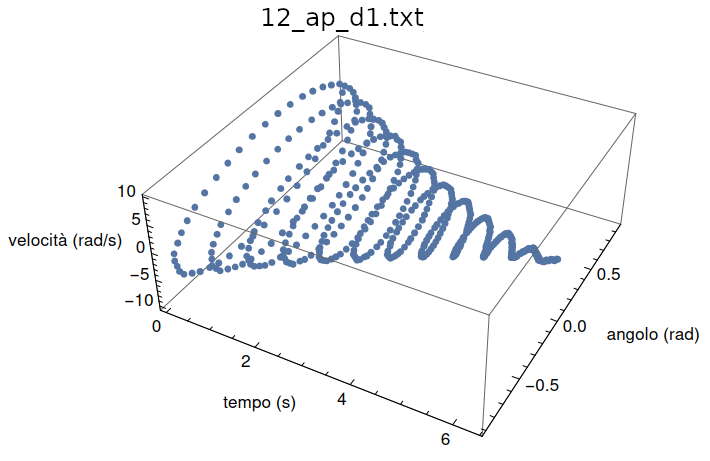
Infine per l'importanza che rivestono nello studio dei sistemi fisici dinamici (ma qui solo per curiosità!), riportiamo le traiettorie nello spazio delle fasi \((\theta,\omega)\) di due prove (figg. 33 e 34): nel caso di attrito viscoso la spirale appare assomigliare ad una spirale logaritmica mentre nel caso di attrito radente l'evidenza è quella di una spirale di Archimede: in entrambi i casi lo stato \((0,0)\) è per i due sistemi un "attrattore".
La medesima rappresentazione con aggiunto l'asse temporale (figg. 35 e 36).
Bibliografia
- X. Wang, C. Schmitt, M. Payne: "Oscillations with three damping effects", European Journal of Physics, p. 155-164 23, 2002.
- G. Torzo, P. Peranzoni: "Il pendolo fisico: teoria, simulazione, esperimento", La fisica nella Scuola, L n. 4, 2017.
- D. Dubin: "Numerical and Analytical Methods for Scientists and Engineers using Mathematica", Wiley.
- C. Mencuccini, V. Silvestrini: "Fisica. Meccanica e Termodinamica", Casa Editrice Ambrosiana.
- P. Mazzoldi, M. Nigro, C. Voci: "Fisica. Vol. 1: Meccanica, Termodinamica", Edises.
Materiali didattici e persone
Di seguito proponiamo i materiali utilizzati per l'elaborazione di tale esperienza e costituiti da
- un foglio di calcolo nel quale riportiamo le quattro prove presentate in questa pagina.
- Associamo a tale foglio pure un notebook di Mathematica che pur non essendo necessario per lo sviluppo dell'elaborazione eseguita su foglio di calcolo è servito per
- affiancare e confermare l'elaborazione fatta su foglio di calcolo,
- trattare in modo automatico un numero maggiore di prove sperimentali,
- automatizzare la ricerca dei valori ottimali per i parametri del modello numerico così come
- ricercare i valori ottimali per le curve inviluppo.
- La traduzione in formato PDF del notebook precedente.
- Un file ZIP con i dati rilevati in 18 prove.
Si ringrazia infine il personale tecnico di laboratorio nella persona del sig. Paolo Giacon per la sua abilità nell'allestire l'apparato ed eseguire i rilievi sperimentali e, non ultime, per la pazienza e la costante disponibilità.