Lisp »Tips 'n Tricks
»Frattali »1 »2 »3 »4 »5 »6 »7
Questi due programmi LISP mostrano come utilizzare le funzioni ricorsive in AutoLISP.
Gli esempi presentano una situazione in cui il programma termina (stop con nc=0), se non è presente uno stop la funzione invoca sé stessa all'infinito cioè una funzione ricorsiva non può essere definita esclusivamente in termini di sé stessa, altrimenti darebbe luogo ad una definizione circolare; quindi una caratteristica essenziale in una definizione ricorsiva è data dalla condizione di terminazione, il cui scopo consiste nel determinare quando una funzione non deve più essere definita in termini di sé stessa.
Quando una funzione viene iterata, cioè quando il risultato di una procedura viene utilizzato come argomento della stessa procedura, questa può convergere verso uno o più valori, indipendentemente dal numero iniziale. Questo valore (o serie di valori) è chiamato attrattore. E dato che per disegnare un frattale si deve iterare una funzione e rappresentare i valori verso i quali converge le figure frattali sono, di fatto, immagini di attrattori.
Un attrattore strano è un modello di un sistema non lineare dinamico caotico.
HNN
;|
HNN.LSP (C) 2005 by Claudio Piccini.
www.cg-cad.com
Disegna l'attrattore strano di Henon
x=y+1-a*x^2
y=b*x
|;
(defun henon ( nc / x1 )
(if (> nc 0)
(progn
(setq x1 x)
(setq x (- (+ y 1)(* a x1 x1)))
(setq y (* b x1))
(if (and (and (< x Xmax)(> x Xmin))(and (< y Ymax)(> y Ymin)))
(command "_point"
(list
(+ (* (- x Xmin) xinc)(car p0)) ; coord. x
(+ (* (- y Ymin) yinc)(cadr p0)) ; coord. y
)
)
)
(setq nc (henon (1- nc)))
)
)
)
(defun c:hnn ( / snapp
Xmin Xmax Ymin Ymax
steps xinc yinc p0
a b x y
)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(setq Xmin -2
Xmax 2
Ymin -2
Ymax 2
x 0
y 0
)
(setq xinc (- Xmax Xmin))
(setq yinc (- Ymax Ymin))
(initget (+ 2 4)) ; non 0 non negativo
(setq steps (getint "\n steps? [10000] "))
(if (= steps nil)(setq steps 10000))
(setq a (getreal "\n a? [1.4] "))
(if (= a nil)(setq a 1.4))
(setq b (getreal "\n b? [0.3] "))
(if (= b nil)(setq b 0.3))
(setq p0 (getpoint "\n clicca un punto:"))
(henon steps)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
Test del lisp
Command: hnn
steps? [10000] Invio
a? [1.4] Invio
b? [0.3] Invio
clicca un punto:

KK
;|
KK.LSP (C) 2005 by Claudio Piccini.
www.cg-cad.com
Disegna l'attrattore della mappa bidimensionale non lineare
x=a*x+y
y=b+x^2
(Kawakami & Kobayashi, 1979)
|;
(defun kawakami_kobayashi ( nc / x1 )
(if (> nc 0)
(progn
(setq x1 x)
(setq x (+ (* a x1) y))
(setq y (+ b (* x1 x1)))
(if (and (and (< x Xmax)(> x Xmin))(and (< y Ymax)(> y Ymin)))
(command "_point"
(list
(+ (* (- x Xmin) xinc)(car p0)) ; coord. x
(+ (* (- y Ymin) yinc)(cadr p0)) ; coord. y
)
)
)
(setq nc (kawakami_kobayashi (1- nc)))
)
)
)
(defun c:kk ( / snapp
Xmin Xmax Ymin Ymax
steps xinc yinc p0
a b x y
)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(setq Xmin -2
Xmax 2
Ymin -2
Ymax 2
x 0
y 0
)
(setq xinc (- Xmax Xmin))
(setq yinc (- Ymax Ymin))
(initget (+ 2 4)) ; non 0 non negativo
(setq steps (getint "\n steps? [10000] "))
(if (= steps nil)(setq steps 10000))
(setq a (getreal "\n a? [-0.1] "))
(if (= a nil)(setq a -0.1))
(setq b (getreal "\n b? [-1.7] "))
(if (= b nil)(setq b -1.7))
(setq p0 (getpoint "\n clicca un punto:"))
(kawakami_kobayashi steps)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
Test del lisp
Command: kk
steps? [10000] Invio
a? [-0.1] Invio
b? [-1.7] Invio
clicca un punto:

Command: kk
steps? [10000] Invio
a? [-0.1] -0.3
b? [-1.7] -1.4
clicca un punto:
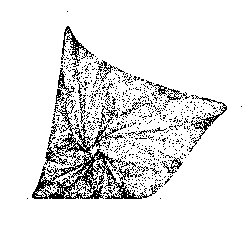
Command: kk
steps? [10000] Invio
a? [-0.1] -0.2
b? [-1.7] -1.2
clicca un punto:

Per approfondire:
Sulle orme del caos, G.I. Bischi, R. Carini, L. Gardini, P. Tenti. Editore Bruno Mondadori.
Dio gioca a dadi?, I. Stewart. Editore Boringhieri.
Computers, pattern, chaos and beauty (cap. 10), C.A. Pickover. Dover Publications, Inc.
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 20 Aprile 2005
|





