Lisp »Tips 'n Tricks »1 »2 »3 »4 »5 »6 »7

Il frattale di Julia (1)

JL4 implementa in AutoLISP l'algoritmo dell'iterazione all'indietro^* per disegnare l'insieme di Julia di z²+c.
Questo metodo disegna un'immagine di Julia, al contrario di JL1, JL2 e JL3 che disegnano solo l'interno o l'esterno dell'insieme.

;|
 JL4 (C)2004 by Claudio Piccini
 12 Aprile 2004
 www.cg-cad.com

 Disegna il frattale di Julia
 con il metodo dell'iterazione all'indietro
|;

;|
 estrae un numero da 0 a 99
|;
(defun rn (sd / m b c)
 (setq m 65521 b 15937 c 33503 sd 
  (rem (+ (* b sd) c) m)
 )
 (setq sd (* (/ sd m) 100))
)

(defun julia ( c1 c2 x0 y0 itera / 
               i sd sx K w0 w1 theta R
 )
 (setq sd 0.0)
 (setq i 1)
 (while (<= i itera)
  (setq w0 (- x0 c1))
  (setq w1 (- y0 c2))
  (if (= w0 0)
   (setq theta (/ pi 2.0))
  )
  (if (> w0 0)
   (setq theta (atan (/ w1 w0)))
  )
  (if (< w0 0)
   (setq theta (+ pi (atan (/ w1 w0))))
  )
  (setq R (sqrt (+ (* w0 w0)(* w1 w1))))
  ; numero casuale
  (setq sx (rn sd))
  (setq K (fix sx))
  (setq sd sx)
  (if (<= K 49)
   (setq K 0)
   (setq K 1)
  )
  ;|
    Sceglie casualmente uno dei due argomenti
    associati alla funzione radice quadrata
    Se K=0 allora l'argomento e' theta/2
    Se K=1 allora l'argomento e' (theta/2)+pi
  |;
  (setq theta (+ (/ theta 2.0) (* K pi)))
  (setq R (sqrt R))
  (setq x0 (* R (cos theta)))
  (setq y0 (* R (sin theta)))
  ;|
    Salta i primi 50 punti
    (dopo averli calcolati)
    per disegnare solo punti vicini a Julia
  |;
  (if (> i 50)
   (progn
    (setq p1 (list x0 y0))
    (command "_point" p1)
   )
  )
  (setq i (1+ i))
 )
)

(defun c:jl4 ( / snapp p1 cx cy itera)
 (setvar "cmdecho" 0)
 (setq snapp (getvar "osmode"))
 (command "_osnap" "_non")
 (initget 1) ;non nil 
 (setq cx (getreal "\nparte reale di c: "))
 (initget 1) ;non nil 
 (setq cy (getreal "\nparte immag. di c: "))
 (initget (+ 2 4)) ;non 0, non negativo 
 (setq itera (getreal "\niterazioni? [15000] "))
 (if (= itera nil)(setq itera 15000))
 (setq p1 (getpoint "\nClicca un punto:"))
 
 (julia cx cy (car p1) (cadr p1) itera)

 (setvar "osmode" snapp)
 (command "_redraw")
 (setvar "cmdecho" 1)
 (princ)
)
;eof

Test del lisp

Command: j4
parte reale di c: -1
parte immag. di c: 0
iterazioni? [15000] 1500
Clicca un punto:

Insieme di Julia di z²-1

Command: jl4
parte reale di c: -1
parte immag. di c: 0
iterazioni? [15000] Invio
Clicca un punto:

Insieme di Julia di z²-1

Command: jl4
parte reale di c: 0
parte immag. di c: -1
iterazioni? [15000] Invio
Clicca un punto:

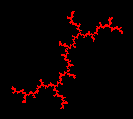Insieme di Julia di z²-i

Command: jl4
parte reale di c: 0.5
parte immag. di c: 0
iterazioni? [15000] Invio
Clicca un punto:

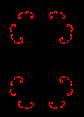Insieme di Julia di z²+0.5

Analisi del lisp

Questo lisp usa i numeri complessi nella loro rappresentazione polare cioè non in forma canonica per calcolare la radice quadrata.
Indicando con x la parte reale e con y la parte immaginaria di un numero complesso e u il cerchio di raggio unitario, si scrive u(Θ)= x+iy che individua un vettore con origine in 0 e l'altro estremo nel punto di coordinate (x,y). La lunghezza del vettore si chiama modulo r del numero complesso e l'angolo che il vettore forma con l'asse reale x si chiama argomento Θ del numero complesso, dato che cos(Θ)=x/r e sen(Θ)=y/r si ottiene la rappresentazione polare di z:
x=r cos(Θ)
y=r sen(Θ)

Il numero complesso z=x+yi si può così scrivere in forma trigonometrica:
z=r(cos(Θ)+sen(Θ)i)

e ottenere le due radici quadrate di z:
z₁=√r cos(Θ/2)+i√r sen(Θ/2)
z₂=-√r cos(Θ/2)-i√r sen(Θ/2), opposto di z₁.

L'istruzione (setq theta (+ (/ theta 2.0) (* K pi))) consente di scegliere (in modo casuale) tra l'argomento Θ/2 e il suo opposto Θ/2+π.

Il lisp IQDR (Autolisp Tips & Tricks volume I) mostra che se il modulo di z è <1 le orbite dei punti tendono al punto fisso 0, se è >1 tendono all'infinito, l'algoritmo dell'iterazione all'indietro suggerisce di calcolare le orbite all'indietro (appunto, a punto a punto) tramite la radice quadrata per disegnare il frattale di Julia di z²+c.

In realtà se paragoniamo Julia di z²+c ad una conchiglia in fondo al mare allora JL1 ne disegna il ripieno, JL2 disegna il ripieno e il mare, JL3 solo il mare mentre JL4 ne disegna (andando indietro nel tempo!) il fossile. Grande Giove!

* Caos e frattali, R.L. Devaney. Editore Addison-Wesley Masson

Lisp »Tips 'n Tricks

Ultimo Aggiornamento_Last Update: 12 Aprile 2004