Lisp »Tips 'n Tricks
»Funzioni ricorsive in AutoLISP
»1
| 2
| 3
| 4
| 5
| 6
| 7 a
, b
, c
, d
, e
>II
>III
>IV
>V
>VI
>VII
Frattali di Julia e Mandelbrot
Per rappresentare i frattali lo schermo 2D del computer deve aprirsi come una finestra sul piano complesso.
Julia
L'insieme di Julia di z²+c (con z e c numeri complessi) è la regione di confine tra l'insieme di punti che fuggono all'infinito e l'insieme di punti attratti da un ciclo, cioè ogni punto del piano complesso con orbita che non fugge all'infinito né è attratta da un ciclo appartiene all'insieme di Julia di z²+c.
L'algoritmo da implementare in autolisp per disegnare l'insieme di Julia di z²+c è il seguente:
- Input: c1 e c2 (numeri reali di c=c1+ic2 parametro complesso di z²+c)
- Input: seleziona una griglia quadrata di punti MxN.
- Per ogni punto z di MxN calcola 20 iterazioni dell'orbita di z controllando se il punto cade fuori dal cerchio di raggio 2.
- Output: se tutti i 20 punti iterati dell'orbita cadono all'interno del cerchio di raggio 2 disegna il punto p(M,N).
Il lisp disegna in nero l'insieme di punti contenuti nel quadrato |x|,|y| <= 2 la cui orbita non esce, prima di 20 iterazioni, dal cerchio con centro nell'origine e raggio 2. Inoltre |c|<=2.
JL1.LSP
;
; JL1 (C)2004 by Claudio Piccini
; 3 Aprile 2004
; www.cg-cad.com
; Disegna il frattale di Julia
;
(defun julia ( itera /
N x0 y0 x y i z
)
(if (>= itera 0)
(progn
(setq x0 (+ -2 (/ itera K))) ;*
(setq N 0)
(while (<= N itera2)
(setq y0 (- 2 (/ N K)))
(setq x x0)
(setq y y0)
(setq i 0)
(while
(progn
(setq i (1+ i))
(setq x1
(+ (- (* x x)(* y y)) cx)
)
(setq y1
(+ (* 2 x y) cy)
)
(setq x x1)
(setq y y1)
(setq z (+ (* x x)(* y y)))
(if (> z 4) nil T)
(if (< i 20) T nil)
)
)
(if (< z 4)
(progn
(command "_point" (list itera N))
(command "_point" (list (- spec itera) (- spec N))) ;*
)
)
(setq N (1+ N))
)
(julia (- itera 1))
)
)
)
(defun c:jl1 ( / snapp cx cy itera itera2 K spec)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget 1) ;non nil
(setq cx (getreal "\nparte reale di c: "))
(initget 1) ;non nil
(setq cy (getreal "\nparte immag. di c: "))
(initget (+ 1 2 4)) ;non nil, non 0, non negativo
(setq itera (getint "\nlato della griglia: "))
(setq spec itera)
(setq itera2 (/ itera 2))
(setq K (/ itera 4.0))
(julia itera)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;eof
|
Test del LISP
Command: jl1
parte reale di c: 0
parte immag. di c: 0
lato della griglia: 100

Insieme di Julia di z²
Command: jl1
parte reale di c: 0.360284
parte immag. di c: 0.100376
lato della griglia: 300

Insieme di Julia di z²+0.360284+0.100376i
Command: jl1
parte reale di c: -1
parte immag. di c: 0
lato della griglia: 300

Insieme di Julia di z²-1
Command: jl1
parte reale di c: -0.1
parte immag. di c: 0.8
lato della griglia: 400

Insieme di Julia di z²-0.1+0.8i
Command: jl1
parte reale di c: -1.25
parte immag. di c: 0
lato della griglia: 400

Insieme di Julia di z²-1.25
Analisi del LISP
(*) Con l'istruzione (setq itera2 (/ itera 2)) divido il lato della griglia per 2 e uso la variabile per il ciclo (while (<= N itera2) sfruttando la simmetria del sistema dinamico: dopo una iterazione le orbite di z e -z sono le stesse, quindi se l'orbita di z tende all'infinito lo stesso accade per -z.
z=(command "_point" (list itera N)) quindi
-z=(command "_point" (list (- spec itera) (- spec N)))
(*) Dalle formule di trasformazione :
M=num_pixel*(x-l)/(r-l)
N=num_pixel*(r-y)/(r-l)
e con (|x|,|y| <= 2), scrivo:
(setq K (/ itera 4.0)) ad es. con itera=M=400, K=100.0
M=400*(x+2)/4
N=400*(2-y)/4
itera=K*(x+2)
N=K*(2-y)
(setq x0 (+ -2 (/ itera K)))
(setq y0 (- 2 (/ N K)))
JL2.LSP
JL2 disegna le orbite in fuga all'infinito, con colori diversi secondo il variare dei tempi di fuga delle orbite.
La regione interna al confine di Julia è colorata in blu: è l'insieme dei punti non caotici, ciclici.
;
; JL2 (C)2004 by Claudio Piccini
; 3 Aprile 2004
; www.cg-cad.com
; Disegna il frattale di Julia
; e i tempi di fuga verso l'infinito
;
(defun julia ( itera /
N x0 y0 x y i z
)
(if (>= itera 0)
(progn
(setq x0 (+ -2 (/ itera K)))
(setq N 0)
(while (<= N itera2)
(setq y0 (- 2 (/ N K)))
(setq x x0)
(setq y y0)
(setq i 0)
(while (< i 20)
(setq x1 (+ (- (* x x)(* y y)) cx))
(setq y1 (+ (* 2 x y) cy))
(setq x x1)
(setq y y1)
(setq z (+ (* x x)(* y y)))
(if (> z 4)
(progn
(cond
((< i 1)(command "_color" "_red"))
((< i 2)(command "_color" "_yellow"))
((< i 4)(command "_color" "_green"))
((< i 20)(command "_color" "_cyan"))
)
(setq i 20)
)
)
(setq i (1+ i))
)
(if (< z 4)(command "_color" "_blue"))
(command "_point" (list itera N))
(command "_point" (list (- spec itera) (- spec N)))
(setq N (1+ N))
)
(julia (- itera 1))
)
)
)
(defun c:jl2 ( / snapp cx cy itera itera2 K spec)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget 1) ;non nil
(setq cx (getreal "\nparte reale di c: "))
(initget 1) ;non nil
(setq cy (getreal "\nparte immag. di c: "))
(initget (+ 1 2 4)) ;non nil, non 0, non negativo
(setq itera (getint "\nlato della griglia: "))
(setq spec itera)
(setq itera2 (/ itera 2))
(setq K (/ itera 4.0))
(julia itera)
(setvar "osmode" snapp)
(command "_color" "_bylayer")
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;eof
|
Test del LISP
Command: jl2
parte reale di c: -1
parte immag. di c: 0
lato della griglia: 400
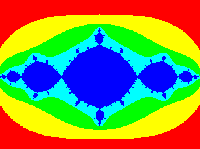
Insieme di Julia di z²-1
JL3.LSP
Con JL3 il tempo per generare il disegno diminuisce perché il lisp non disegna la regione interna al confine di Julia.
;
; JL3 (C)2004 by Claudio Piccini
; 4 Aprile 2004
; www.cg-cad.com
; Disegna il frattale di Julia
; e i tempi di fuga verso l'infinito
;
(defun julia ( itera /
N x0 y0 x y i z
)
(if (>= itera 0)
(progn
(setq x0 (+ -2 (/ itera K)))
(setq N 0)
(while (<= N itera2)
(setq y0 (- 2 (/ N K)))
(setq x x0)
(setq y y0)
(setq i 0)
(while (< i 20)
(setq x1 (+ (- (* x x)(* y y)) cx))
(setq y1 (+ (* 2 x y) cy))
(setq x x1)
(setq y y1)
(setq z (+ (* x x)(* y y)))
(if (> z 4)
(progn
(cond
((< i 1)(command "_color" "_red"))
((< i 4)(command "_color" "_yellow"))
((< i 8)(command "_color" "_green"))
((< i 10)(command "_color" "_cyan"))
((< i 20)(command "_color" "_blue"))
)
(setq i 20)
)
)
(setq i (1+ i))
)
(if (> z 4)
(progn
(command "_point" (list itera N))
(command "_point"
(list (- spec itera)(- spec N))
)
)
)
(setq N (1+ N))
)
(julia (- itera 1))
)
)
)
(defun c:jl3 ( / snapp cx cy itera itera2 K spec)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget 1) ;non nil
(setq cx (getreal "\nparte reale di c: "))
(initget 1) ;non nil
(setq cy (getreal "\nparte immag. di c: "))
(initget (+ 1 2 4)) ;non nil, non 0, non negativo
(setq itera (getint "\nlato della griglia: "))
(setq spec itera)
(setq itera2 (/ itera 2))
(setq K (/ itera 4.0))
(julia itera)
(setvar "osmode" snapp)
(command "_color" "_bylayer")
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;eof
|
Mandelbrot
Prima si è visto il ruolo giocato dall'orbita di 0 nella ricerca di cicli attrattori per f(x)=x²+c; in conseguenza di ciò tale orbita è chiamata orbita critica e 0 punto critico.
Nel piano complesso l'insieme dei valori di c per cui l'orbita critica di z²+c non tende all'infinito è detto insieme di Mandelbrot.
Per disegnare l'insieme si deve calcolare l'orbita di 0 per n iterazioni e per ogni punto vedere se il modulo è maggiore di 2, cioè se l'orbita è al di fuori del cerchio di raggio 2 allora sfugge all'infinito e quindi non appartiene all'insieme.
Ecco i passi dell'algoritmo:
- Seleziona una griglia quadrata di punti MxN.
- Leggi ogni punto della griglia come un valore di c.
- Per ogni c calcola 30 iterazioni dell'orbita di 0 e vedi se sfugge all'infinito altrimenti disegna il punto.
MANB.LSP
;
; manb.lsp (C)2004 by Claudio Piccini
; 4 Aprile 2004
; www.cg-cad.com
; Disegna il frattale di Mandelbrot
;
(defun mandelbrot ( itera / N cx cy x y x1 y1 R i )
(if (>= itera 0)
(progn
(setq N 0)
(while (<= N itera2)
(setq cx (+ -2 (/ itera K)))
(setq cy (- 2 (/ N K)))
(setq x cx)
(setq y cy)
(setq i 0)
(while
(progn
(setq i (1+ i))
(setq x1 (+ (- (* x x)(* y y)) cx))
(setq y1 (+ (* 2 x y) cy))
(setq R (+ (* x1 x1)(* y1 y1)))
(setq x x1)
(setq y y1)
(if (> R 4) nil T)
(if (< i 30) T nil)
)
)
(if (< R 4)
(progn
(command "_point" (list itera N))
(command "_point" (list itera (- spec N))
)
)
)
(setq N (1+ N))
)
(mandelbrot (- itera 1))
)
)
)
(defun c:manb ( / snapp itera itera2 K spec)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget (+ 1 2 4)) ;non nil, non 0, non negativo
(setq itera (getint "\nlato della griglia: "))
(setq spec itera)
(setq itera2 (/ itera 2))
(setq K (/ itera 4.0))
(mandelbrot itera)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;eof
|
Test del LISP
Command: manb
lato della griglia: 300

Insieme di Mandelbrot
L'insieme di M nella tipica forma a cuore con isole puntiformi attorno...
MANB2.LSP
MANB2 disegna solo le orbite in fuga all'infinito, con colori diversi secondo il variare dei tempi di fuga delle orbite.
;
; manb2.lsp (C)2004 by Claudio Piccini
; 4 Aprile 2004
; www.cg-cad.com
; Disegna il frattale di Mandelbrot
;
(defun mandelbrot ( itera /
N cx cy x y x1 y1 R i
)
(if (>= itera 0)
(progn
(setq N 0)
(while (<= N itera2)
(setq cx (+ -2 (/ itera K)))
(setq cy (- 2 (/ N K)))
(setq x cx)
(setq y cy)
(setq i 0)
(while (< i 30)
(setq x1 (+ (- (* x x)(* y y)) cx))
(setq y1 (+ (* 2 x y) cy))
(setq R (+ (* x1 x1)(* y1 y1)))
(setq x x1)
(setq y y1)
(if (> R 4)
(progn
(cond
((< i 1)(command "_color" "_red"))
((< i 4)(command "_color" "_yellow"))
((< i 8)(command "_color" "_green"))
((< i 10)(command "_color" "_cyan"))
((< i 30)(command "_color" "_blue"))
)
(setq i 30)
)
)
(setq i (1+ i))
)
(if (> R 4)
(progn
(command "_point" (list itera N))
(command "_point" (list itera (- spec N))
)
)
)
(setq N (1+ N))
)
(mandelbrot (- itera 1))
)
)
)
(defun c:manb2 ( / snapp itera itera2 K spec)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget (+ 1 2 4)) ;non nil, non 0, non negativo
(setq itera (getint "\nlato della griglia: "))
(setq spec itera)
(setq itera2 (/ itera 2))
(setq K (/ itera 4.0))
(mandelbrot itera)
(setvar "osmode" snapp)
(command "_color" "_bylayer")
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;eof
|
Test del LISP
Command: manb2
lato della griglia: 400

Il colore blu dichiara che le isole puntiformi sono in realtà connesse al cuore dell'insieme.
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 5 Aprile 2004
|

