Lisp »Tips 'n Tricks
»Funzioni ricorsive in AutoLISP
»1
| 2
| 3
| 4
| 5
| 6
| 7 a
, b
, c
, d
, e
>II
>III
>IV
>V
>VI
>VII
Orbite, punti fissi e periodici
Con ITR è possibile iterare il calcolo di funzioni f(x): il lisp mostra l'indice di iterazione e i relativi valori.
Iterare consiste nell'inserire, ad esempio in una calcolatrice, un numero x, e quindi premere ripetutamente uno di quei tasti speciali, ad esempio sqrt.
;;;
;;; Itr.lsp - 23 Marzo 2004
;;; (C) 2004 by Claudio Piccini.
;;; www.cg-cad.com
;;;
;;; Itera n volte il calcolo di F(x)
;;;
(defun itera ( x n / y )
(if (> n 0)
(progn
(setq y (eval funzione))
(setq conta (1+ conta))
(setq str (strcat "\nF" (itoa conta) "(" cx ")=" (rtos y 2 6)))
(princ str)
(setq x y)
(itera x (- n 1))
)
)
)
(defun c:itr ( / f x n funzione conta cx )
(setq conta 0)
(setq f (getstring "\nFunzione (ad es. \"(sin x)\"): "))
(setq x (getreal "\nNumero da iterare: "))
(setq cx (rtos x 2 6))
(setq n (getint "\nQuante iterazioni? "))
(setq funzione (read f))
(itera x n)
(princ)
)
;;;eof
|
Test del LISP
Command: itr
Funzione (ad es. "(sin x)"): "(sqrt x)"
Numero? 0.5
Iterazioni? 100
F1(0.5)=0.707107
F2(0.5)=0.840896
F3(0.5)=0.917004
F4(0.5)=0.957603
F5(0.5)=0.978572
...
F20(0.5)=0.999999
F21(0.5)=1
...
F100(0.5)=1
Command: itr
Funzione (ad es. "(sin x)"): "(sqrt x)"
Numero? 11074
Iterazioni? 100
F1(11074)=105.233075
F2(11074)=10.258317
F3(11074)=3.202861
F4(11074)=1.789654
F5(11074)=1.337779
...
F24(11074)=1.000001
F25(11074)=1
...
F100(11074)=1
Anche con valori diversi il risultato di (sqrt x) tende sempre a 1 (→1).
L'insieme delle successive iterazioni di un numero (o di un punto) viene chiamato orbita di quel punto.
L'orbita di 0.5 relativa a F(x)=(sqrt x) è la successione 0.5, 0.707107, 0.840896, ...→1.
L'orbita di 2 relativa a F(x)=x² è la successione 2, 4, 16, 256, ... →∞.
L'orbita di x>1 relativa a F(x)=x² è sempre →∞.
L'orbita di 0<x<1 relativa a F(x)=x² è sempre →0.
Esistono numeri che con certe funzioni per qualsiasi numero di iterazioni non orbitano ma restano fissi, e sono detti punti fissi.
Ad esempio F(x)=x² con x=1 Fn(x)=1.
0 e 1 sono punti fissi di (sqrt x).
ITR descrive quindi un sistema dinamico: il numero si sposta, orbita. Ma non tutte le orbite tendono ad un punto fisso o all'infinito: un diverso tipo di orbita è l'orbita periodica o ciclo.
Command: itr
Funzione (ad es. "(sin x)"): "(/ 1 x)"
Numero? 1.1
Iterazioni? 10
F1(1.1)=0.909091
F2(1.1)=1.1
F3(1.1)=0.909091
F4(1.1)=1.1
F5(1.1)=0.909091
...
F9(1.1)=0.909091
F10(1.1)=1.1
Command: itr
Funzione (ad es. "(sin x)"): "(/ 1 x)"
Numero? 23
Iterazioni? 25
F1(23)=0.043478
F2(23)=23
F3(23)=0.043478
F4(23)=23
...
F24(23)=23
F25(23)=0.043478
Command: itr
Funzione (ad es. "(sin x)"): "(/ 1 x)"
Numero? -0.4
Iterazioni? 100
F1(-0.4)=-2.5
F2(-0.4)=-0.4
F3(-0.4)=-2.5
F4(-0.4)=-0.4
F5(-0.4)=-2.5
F6(-0.4)=-0.4
...
F99(-0.4)=-2.5
F100(-0.4)=-0.4
Un orbita è periodica se dopo un certo numero di iterazioni ritorna al punto di partenza, nell'esempio tutti i numeri diversi da zero sono periodici (con periodo 2) esclusi 1 e -1 (punti fissi) di 1/x.
Altro esempio con la funzione cx(1-x) e c=3.5 l'orbita di 0.5 è attratta da un ciclo di periodo 4:
Command: itr
Funzione (ad es. "(sin x)"): "(*(* 3.5 x)(- 1 x))"
Numero? 0.5
Iterazioni? 100
F1(0.5)=0.875
F2(0.5)=0.382813
F3(0.5)=0.826935
F4(0.5)=0.500898
F5(0.5)=0.874997
F6(0.5)=0.38282
F7(0.5)=0.826941
F8(0.5)=0.500884
F9(0.5)=0.874997
F10(0.5)=0.38282
F11(0.5)=0.826941
F12(0.5)=0.500884
F13(0.5)=0.874997
F14(0.5)=0.38282
F15(0.5)=0.826941
F16(0.5)=0.500884
...
F96(0.5)=0.500884
F97(0.5)=0.874997
F98(0.5)=0.38282
F99(0.5)=0.826941
F100(0.5)=0.500884
ITRG disegna il grafico delle orbite di f(x).
;;;
;;; Itrg.lsp - 26 Marzo 2004
;;; (C) 2004 by Claudio Piccini.
;;; www.cg-cad.com
;;;
;;; Itera il calcolo di funzioni f(x)
;;; e ne disegna il grafico
;;;
(defun itera ( x n / y )
(if (> n 0)
(progn
(setq y (eval funzione))
(command "_point" (list x y 0))
(setq x y)
(itera x (- n 1))
)
)
)
(defun c:itrg ( / f x n funzione)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(setq f (getstring "\nFunzione (ad es. \"(sin x)\"): "))
(setq x (getreal "\nNumero? "))
(setq n (getint "\nIterazioni? "))
(setq funzione (read f))
(itera x n)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
Test del LISP
Command: itrg
Funzione (ad es. "(sin x)"): "(*(* 3.5 x)(- 1 x))"
Numero? 0.5
Iterazioni? 100
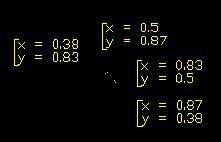
Command: itrg
Funzione (ad es. "(sin x)"): "(*(* 4 x)(- 1 x))"
Numero? 0.1
Iterazioni? 100

Link e manuali
Caos e frattali, R.L. Devaney. Editore Addison-Wesley Masson
Caos e oggetti frattali
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 26 Marzo 2004
|