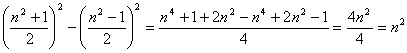QUESITO N. 3   Si tratta di un'equazione di secondo grado i cui coefficienti possono essere scritti come:   a = 103                     b = 108 - 1                       c= - 105   il discriminante sarà quindi:  =  =         =   e pertanto le due soluzioni saranno:         Una soluzione ancora più “elegante” è stata proposta da Gianluca ed utilizza la scomposizione in fattori mediante il raccoglimento parziale:     L’equazione può essere scritta così:

QUESITO N. 4   La dimostrazione è la seguente: i due numeri naturali consecutivi sono n-1  e  n, la differenza tra i quadrati sarà n² - (n - 1)² = n² - (n² - 2n +1) = n² - n² + 2n - 1 = 2n -1 e 2n - 1 è certamente un numero dispari in quanto 2n è sicuramente un numero pari essendo un multiplo di 2.

GIOCO N. 1 Il trucco è stato quello di ammettere che se (x + 1) ² = x²  allora x + 1 = x  il che non è sempre vero in quanto mentre i quadrati sono sempre positivi, le basi potrebbero non esserlo.