



Teorema dell'esistenza degli zeri
Teorema dell'esistenza degli zeri: Se una funzione f(x) è continua in un intervallo [a,b], e se
risulta f(a)= - f(b), allora esiste in [a,b] almeno un punto Xo tale che f(Xo)=0.
 verifica: Tale proprietà può essere facilmente compresa se si pensa che una funzione continua può
essere tracciata senza staccare la penna dal foglio.
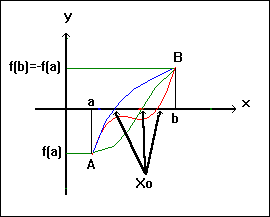
Facendo riferimento alla figura, in cui sono tracciate tre funzioni in colore, si vede chiaramente che,
quale che sia l'andamento della funzione, se essa deve congiungere i due punti A=(a,f(a)) e B=(b,-f(a)),
deve necessariamente tagliare l'asse delle x in un punto Xo, dove si avrà che f(Xo)=0.
verifica: Tale proprietà può essere facilmente compresa se si pensa che una funzione continua può
essere tracciata senza staccare la penna dal foglio.
Facendo riferimento alla figura, in cui sono tracciate tre funzioni in colore, si vede chiaramente che,
quale che sia l'andamento della funzione, se essa deve congiungere i due punti A=(a,f(a)) e B=(b,-f(a)),
deve necessariamente tagliare l'asse delle x in un punto Xo, dove si avrà che f(Xo)=0.
 verifica: Tale proprietà può essere facilmente compresa se si pensa che una funzione continua può
essere tracciata senza staccare la penna dal foglio.
Facendo riferimento alla figura, in cui sono tracciate tre funzioni in colore, si vede chiaramente che,
quale che sia l'andamento della funzione, se essa deve congiungere i due punti A=(a,f(a)) e B=(b,-f(a)),
deve necessariamente tagliare l'asse delle x in un punto Xo, dove si avrà che f(Xo)=0.
verifica: Tale proprietà può essere facilmente compresa se si pensa che una funzione continua può
essere tracciata senza staccare la penna dal foglio.
Facendo riferimento alla figura, in cui sono tracciate tre funzioni in colore, si vede chiaramente che,
quale che sia l'andamento della funzione, se essa deve congiungere i due punti A=(a,f(a)) e B=(b,-f(a)),
deve necessariamente tagliare l'asse delle x in un punto Xo, dove si avrà che f(Xo)=0.



