Teorema del valore centrale

Teorema: Se una funzione f(x) è continua in un intervallo [a,b], e se risulta f(a)=A e f(b)=B con A diverso da B, allora quale che sia il numero C compreso tra A e B, si può trovare un punto x=Xo compreso in [a,b] tale che f(Xo)=C
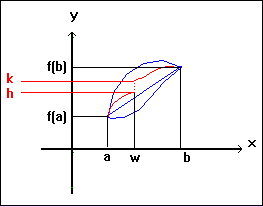verifica: analogamente al caso precedente si vede facilmente che se la funzione unisce con continuità i due punti estremi essa assume tutti i valori tra f(a) e f(b). Delle quattro funzioni disegnate in figura quella in rosso non assume i valori compresi tra h e k, ma essa è evidentemente discontinua nel punto w.

---