| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. |  |
| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. | |
Proposte le definizioni di punto e triangolo pedale si determinano le lunghezze dei lati del triangolo pedale in funzione delle distanze dai vertici del triangolo originario. Si dimostra poi una curiosa proprietà di tali triangoli.
Nelle pagine precedenti abbiamo più volte discusso di vari tipi di triangoli associati ad un triangolo qualsiasi: in particolare si sono dimostrate e utilizzate le proprietà del triangolo costituito dai piedi delle altezze e di quello avente per vertici i punti medi dei lati.
Qui proporremo una definizione che comprenda questi due casi e ne generalizzi alcune loro caratteristiche. Sia quindi P un punto interno ad un dato 
ABC. Condotte da P le perpendicolari ai lati, siano A1, B1 e C1 le intersezioni di queste, rispettivamente con i lati BC, CA e AB (fig. 1).
figura 1
ABC, il punto P, interno a ABC.Sia in questa definizione che in quanto verrà discusso in questa pagina considereremo che P sia un punto interno al triangolo: più avanti estenderemo la definizione a qualsiasi punto del piano contenente il triangolo. Tenendo presente come sono stati ottenuti i punti A1, B1 e C1 possiamo far seguire un'altra
A1B1C1 dicesi triangolo pedale di ABC di origine P.Da queste definizioni segue che il triangolo avente per vertici i piedi delle altezze è un triangolo pedale che si origina dall'ortocentro (quando questo è interno) così come il triangolo costruito sui punti medi, rientra tra i triangoli pedali con origine nel circocentro di ABC.
In base alla figura 2, essendo 
AB1P = AC1P = 90°, i punti A, C1, P e B1 appartengono ad un cerchio di diametro AP, ossia P appartiene alla circonferenza circoscritta a AC1B1.
figura 2
Applicando il teorema dei seni ai triangoli AC1B1 e ABC, otteniamo
| B1C1 sen A |
= | AP | BC sen A |
= | 2·rc |
con rc raggio del cerchio circoscritto a ABC. Eliminando senA da entrambe e, posto al solito, BC = a, deduciamo
| B1C1 | = | a· | AP 2·rc |
che mette in evidenza come la lunghezza del lato B1C1 del triangolo pedale dipenda essenzialmente dalla distanza AP del punto pedale P dal vertice A. Poiché si può procedere nello stesso modo anche rispetto ai rimanenti vertici, possiamo affermare il seguente
ABC sono date dalle
|
Evidentemente, nel caso che P coincida con il circocentro AP = BP = CP = rc si riottiene il caso già esposto dove le lunghezze dei lati risultano la metà di quelle di ABC.
Dimostriamo ora un curioso teorema, pubblicato per la prima volta nel 1892 da John Casey. Innanzitutto osserviamo come, preso un punto P come pedale di ABC, sia possibile costruire una successione di triangoli pedali.
figura 3
La figura 3 mostra come, dal medesimo punto pedale P, tracciando ancora le perpendicolari ai lati A1B1, B1C1 e C1A1 si possa ottenere un secondo triangolo A2B2C2, pedale di A1B1C1. Nello stesso modo, partendo da A2B2C2, si può ottenere un terzo triangolo pedale A3B3C3 (fig. 4).
figura 4
Dimostriamo quindi
A3B3C3 è simile al triangolo di partenza ABC.Come detto il quadrilatero AC1PB1 è inscritto in un cerchio per cui C1AP = C1B1P = A2B1P essendo angoli alla circonferenza che insistono sullo stesso arco (fig. 5a).
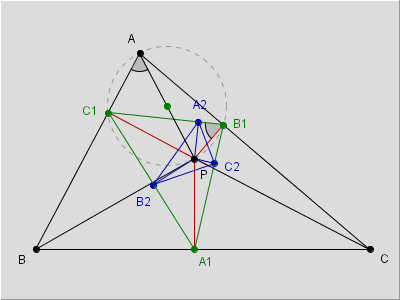
figura 5a |
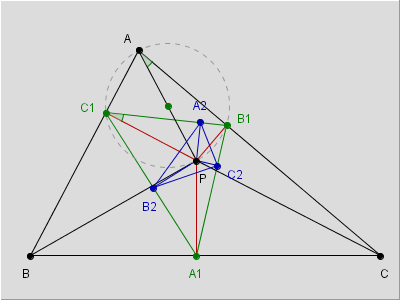
figura 5b |
D'altra parte P appartiene pure al cerchio che contiene il quadrilatero A2B1C2P (la fig. 6a è ingrandita rispetto alle precedenti: dopo aver fatto clic sulla figura, si usino i tasti + e - della tastierina numerica per ingrandire o rimpicciolire la figura oppure 
)
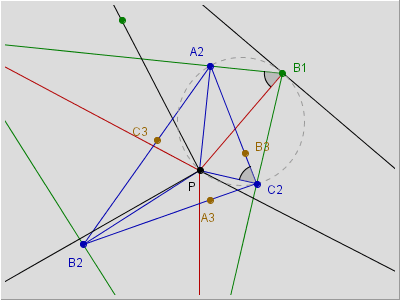
figura 6a |
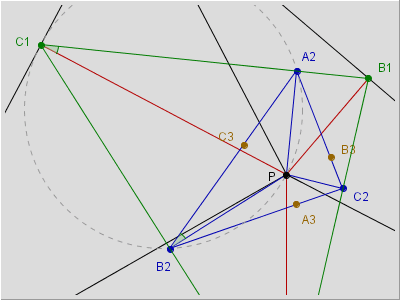
figura 6b |
per cui, per lo stesso motivo risulta A2B1P = A2C2P = B3C2P (fig. 6a).
Infine risulta B3C2P = B3A3P (fig. 7a). In sostanza, tenendo conto della catena di congruenze, per transitività abbiamo che
C1AP = B3A3P.
In modo del tutto analogo si può dimostrare che (figg. 5b, 6b, 7b)
PAB1 = PC1B1 = PC1A2 = PB2A2 = PB2C3 = PA3C3
ossia le due parti nelle quali AP divide A si ritrovano, separatamente nel primo triangolo pedale in B1 e C1 (figg. 5ab), ancora separatamente nel secondo in C2 e B2 (figg. 6ab) e finalmente nel terzo sono assieme in A3 (figg. 7ab). Pertanto BAC = B3A3C3.
Immediata è l'estensione di quanto detto anche agli altri angoli di ABC per cui risulta dimostrato che ABC
A3B3C3.
La figura successiva intende evidenziare questa proprietà. In essa appaiono (approssimati) i valori delle ampiezze degli angoli di ABC e, a parte, le misure delle ampiezze degli angoli di A3B3C3.
Per ottenere ciò si sono preventivamente definiti tutti gli angoli e quindi per quelli di A3B3C3 si sono richieste le relative misure. Per accedere alla finestra associata allo strumento espressione algebrica 
e vedere come queste grandezze siano state immesse nella stessa, si selezioni 
e si faccia un clic sulle relative espressioni: nella cella Espressione aritmetica apparirà il nome simbolico dell'angolo e in quella sopra una breve spiegazione.
Comunque, muovendo nella figura uno qualsiasi dei vertici di ABC gli angoli di quest'ultimo variano ma rimangono uguali a quelli di A3B3C3 che variano a loro volta. Trascinando invece il punto pedale P non varia alcun angolo di A3B3C3 (né quelli, ovviamente, di ABC).
figura 8
Costruzione 4.1. Costruire un quadrilatero qualsiasi e il suo quarto quadrilatero pedale. Verificare che quest'ultimo è simile a quello di origine.
Costruzione
In effetti con quanto suggerito sopra si vuole proporre una evidente generalizzazione. B. M. Stewart ha difatti dimostrato nel 1940 che
| Ricarica la pagina con le figure interattive: attendere il caricamento di un file di 1,2 Mb. | |
|
||||||||||
