L'astroide
- Definizione e notizie storiche
- Prima costruzione
- Equazioni rappresentative
- L'astroide come inviluppo di ellissi
Definizione e notizie storiche
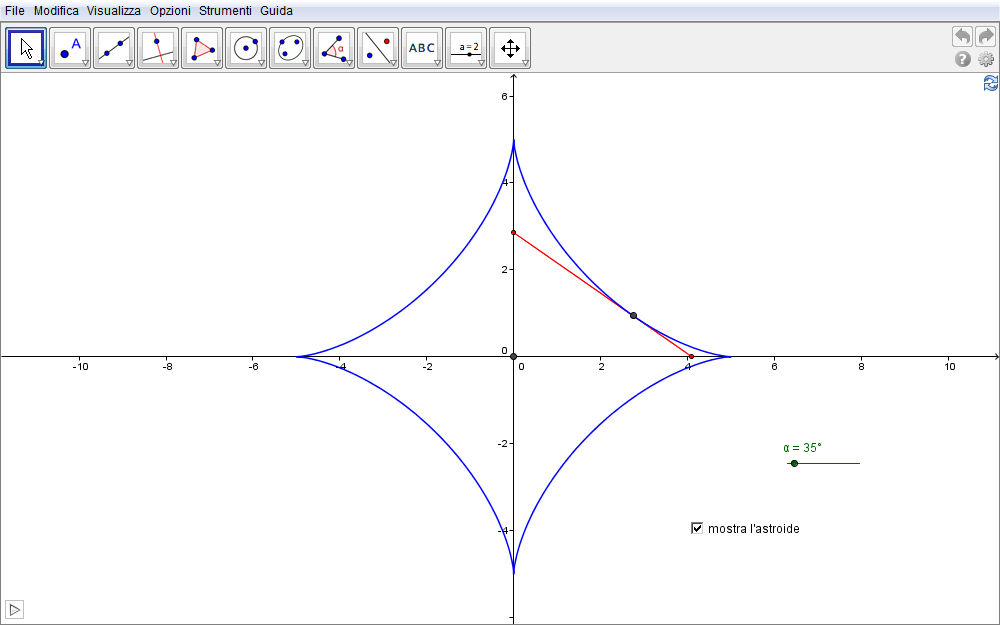
L'astroide, curva a quattro cuspidi detta pure asteroide, cubocicloide e paraciclo, si ottiene come l'inviluppo di un segmento di lunghezza fissa ED (trascinare lo slider \(\alpha\) o avviare l'animazione in fig. 3.1) i cui estremi scorrano su due assi ortogonali. Ciò significa che il segmento ED compreso tra le rette perpendicolari individua in ogni sua possibile posizione la retta tangente ad un punto F dell'astroide. Questo punto di contatto tra retta tangente e astroide risulta essere il piede dell'altezza relativa all'ipotenusa ED condotta dal vertice C del triangolo EDC (fig. 3.2).
Il nome di astroide compare per la prima volta in un libro pubblicato a Vienna nel 1838 ma la curva era già nota a Leibniz fin dal 1715.
Figura 3.1. astroide01.ggb.
Prima costruzione
La classica costruzione dell'astroide richiede i passi seguenti: in riferimento alla fig. 3.2
Figura 3.2. astroide02.ggb.
- definiti i punti \(A(0,0)\) e \(B(5,0)\),
- tracciare la circonferenza c di centro A e raggio \(AB\) (nella figura \(AB= 5\)).
- Definire un punto qualsiasi C di questa circonferenza,
- tracciare le rette per C perpendicolari rispettivamente all'asse x all'asse y.
- Queste permettono di individuare i punti D ed E, proiezioni di C sui due assi.
- Costruito il segmento \(ED\) che, in quanto diagonale del rettangolo \(ADCE\) possiede lunghezza costante pari all'altra diagonale \(AC\) ossia, \(ED=AC\), sia
- e la retta per C perpendicolare ad \(ED\) e
- F il punto di intersezione di questa con \(ED\). È questo il punto che appartiene all'astroide mentre \(ED\) individua la direzione della tangente in F a tale curva.
- Per visualizzare infine il luogo dei punti F, utilizzare lo strumento Luogo
 fornendo come primo punto F e come secondo il punto C, variabile sulla circonferenza.
fornendo come primo punto F e come secondo il punto C, variabile sulla circonferenza.
Trascinando nella fig. 3.2 il punto C è immediato constatare come F giaccia sempre sulla curva astroide.
Equazioni rappresentative
Dalla costruzione proposta e al fine di determinare le equazioni rappresentative per il punto \(F(x,y)\), appare naturale individuare come parametro l'angolo \(\theta=\angle(BAC)\) (fig. 3.2). Detto r il raggio della circonferenza centrata in A, C è individuato univocamente dalle coordinate \begin{equation}C(x_C,y_C)=(r\cos\theta,r\sin\theta).\label{eq:uno}\end{equation} mentre le sue proiezioni possiedono coordinate \begin{equation}D(x_D,y_D)=D(r\cos\theta,0),\qquad E(x_E,y_E)=E(0,r\sin\theta).\end{equation} Il coefficiente angolare della retta \(ED\) risulta \begin{equation}m_{ED}={y_E-y_D\over x_E-x_D}={r\sin\theta-0\over 0-r\cos\theta}=-\tan\theta\label{eq:tre}\end{equation} e la sua equazione \begin{equation}y-y_E=m_{ED}(x-x_E)\quad\Rightarrow\quad y=-x\tan\theta+r\sin\theta.\label{eq:rettaED}\end{equation} La retta per C e F, perpendicolare a \(ED\), avrà equazione \begin{equation}CF:y-y_C=-{1\over m_{ED}}(x-x_C)\end{equation} che per le \eqref{eq:uno} e \eqref{eq:tre} diviene \begin{equation}CF: y-r\sin\theta={1\over \tan\theta}(x-r\cos\theta)\quad\Rightarrow\quad y=x\biggl({\cos\theta\over\sin\theta}\biggr)+r\sin\theta-r\biggl({\cos^2\theta\over\sin\theta}\biggr).\label{eq:sei}\end{equation}
Il punto F discende ora dal sistema (di I grado) di \eqref{eq:rettaED} con \eqref{eq:sei} \begin{equation}\cases{y=-x\tan\theta+r\sin\theta\cr\vphantom{x}\cr y=x\biggl({\cos\theta\over\sin\theta}\biggr)+r\sin\theta-r\biggl({\cos^2\theta\over\sin\theta}\biggr)\cr}\label{eq:sistema}\end{equation} e conduce all'equazione \begin{equation}-x\tan\theta+r\sin\theta= x\biggl({\cos\theta\over\sin\theta}\biggr)+r\sin\theta-r\biggl({\cos^2\theta\over\sin\theta}\biggr)\quad\Rightarrow\quad x\tan\theta+x\biggl({\cos\theta\over\sin\theta}\biggr)= r\biggl({\cos^2\theta\over\sin\theta}\biggr)\end{equation} dalla quale con alcuni passaggi algebrici e sfruttando l'identità goniometrica fondamentale, otteniamo \begin{equation}x\biggl({\sin\theta\over\cos\theta}+{\cos\theta\over\sin\theta}\biggr)=r\biggl({\cos^2\theta\over\sin\theta}\biggr)\quad\Rightarrow\quad x\biggl({\sin^2\theta+\cos^2\theta\over \sin\theta\cos\theta}\biggr)=r\biggl({\cos^2\theta\over\sin\theta}\biggr)\quad\Rightarrow\quad x\biggl({1\over \sin\theta\cos\theta}\biggr)=r\biggl({\cos^2\theta\over\sin\theta}\biggr).\end{equation} La moltiplicazione per \(\sin\theta\cos\theta\) fornisce quindi\begin{equation}x=r\cos^3\theta.\end{equation} Sostituita quest'ultima nella prima delle \eqref{eq:sistema} \begin{equation}y=-r\cos^3\theta\cdot{\sin\theta\over\cos\theta}+r\sin\theta=-r\cos^2\theta\sin\theta+r\sin\theta\end{equation} si giunge alla \begin{equation}y=r\sin\theta(1-\cos^2\theta)=r\sin^3\theta.\end{equation} In definitiva le equazioni parametriche dell'astroide in termini del parametro \(\theta\) sono \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x=r\cos^3\theta\cr y=r\sin^3\theta.}}\label{eq:parametriche01}\end{equation}
Dalle precedenti è immediato isolare i termini goniometrici \begin{equation}\cases{{x\over r}=\cos^3\theta\cr\vphantom{x}\cr {y\over r}=\sin^3\theta\cr}\end{equation} e quindi, l'estrazione della radice cubica conduce alle equazioni \begin{equation}\cases{\biggl({x\over r}\biggr)^{\kern-2pt1/3}=\cos\theta\cr\vphantom{x}\cr \biggl({y\over r}\biggr)^{\kern-2pt 1/3}=\sin\theta.\cr}\label{eq:quindici}\end{equation} Elevando al quadrato tutti i membri delle \eqref{eq:quindici} e sommandoli si ottiene \begin{equation}\biggl({x\over r}\biggr)^{\kern-2pt2/3}\kern-3pt+\biggl({y\over r}\biggr)^{\kern-2pt 2/3}\kern-5pt=\cos^2\theta+\sin^2\theta\quad\Rightarrow\quad \biggl({x\over r}\biggr)^{\kern-2pt2/3}\kern-3pt+\biggl({y\over r}\biggr)^{\kern-2pt 2/3}=1\label{eq:16}\end{equation} e dove si è tenuto conto dell'identità goniometrica fondamentale. Infine, moltiplicando per \(r^{2/3}\) si giunge all'equazione cartesiana implicita dell'astroide \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{x^{2/3}+y^{2/3}=r^{2/3}.}\label{eq:17}\end{equation}
Otteniamo una diversa rappresentazione se come parametro scegliamo l'ascissa \(t=x_D=r\cos\theta\) del punto D. Ne discende che \begin{equation}\cos\theta={t\over r}\quad -r\leq t\leq r\end{equation} che sostituita nella prima delle \eqref{eq:quindici} fornisce \begin{equation}\biggl({x\over r}\biggr)^{\kern-2pt 1/3}={t\over r}\quad\Rightarrow\quad {x\over r}={t^3\over r^3}\quad\Rightarrow\quad x={t^3\over r^2}.\label{eq:19}\end{equation} Per ottenere l'ordinata sostituiamo la seconda delle \eqref{eq:19} nella \eqref{eq:16} \begin{equation}{t^2\over r^2}+\biggl({y\over r}\biggr)^{\kern-2pt 2/3}=1\end{equation} da cui \begin{equation}\biggl({y\over r}\biggr)^{\kern-2pt 2/3}=1-{t^2\over r^2}\quad\Rightarrow\quad \biggl({y\over r}\biggr)^{\kern-2pt 2/3}={r^2-t^2\over r^2}.\end{equation} Elevando al cubo entrambi i membri risulta \begin{equation}\biggl({y\over r}\biggr)^{\kern-2pt 2}=\biggl({r^2-t^2\over r^2}\biggr)^{\kern-2pt 3}\quad\Rightarrow\quad {y^2\over r^2}=\biggl({r^2-t^2\over r^2}\biggr)^{\kern-2pt 3}\end{equation} da cui \begin{equation}y^2={(r^2-t^2)^3\over r^4}\end{equation} cosicché l'estrazione della radice quadrata fornisce \begin{equation}\bigl|\,y\,\bigr|={\sqrt{(r^2-t^2)^3}\over r^2}.\end{equation} In definitiva la rappresentazione alternativa che abbiamo ottenuto si riassume nella coppia di equazioni \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={t^3\over r^2},\quad -r\leq t\leq r\cr\vphantom{x}\cr\bigl|\,y\,\bigr|={\sqrt{(r^2-t^2)^3}\over r^2}.\cr}}\end{equation}
L'astroide come inviluppo di ellissi
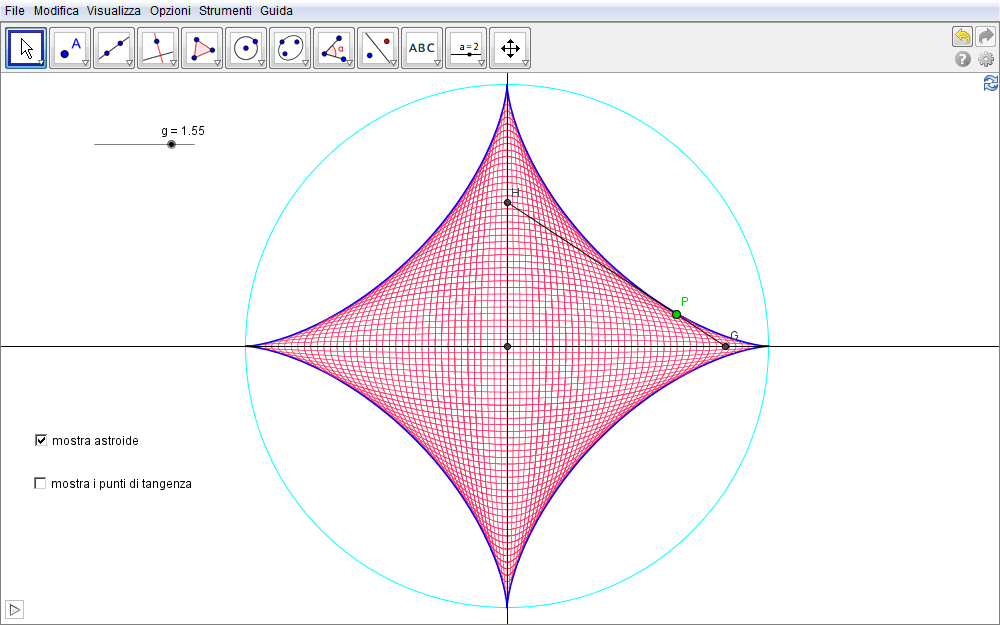
Come visto a riguardo dell'ellisse, l'astroide si può ottenere pure come l'inviluppo di un famiglia di ellissi centrate aventi la somma dei due semiassi costante e pari ad r.
Figura 3.3. astroide03.ggb.
L'animazione nella fig. 3.3 mette in evidenza questo fatto: ogni punto P del segmento mobile \(HG\) al variare di F (lo si trascini) appartiene ad una ellisse con la somma dei semiassi pari ad r (nella figura è \(r=2\)). Il punto medio di \(HG\), in particolare, appartiene ad una circonferenza di raggio \(r/2\) (si riporti lo slider al valore 1). Ciascuna ellisse di questa famiglia tocca l'astroide in quattro punti simmetrici rispetto agli assi: in questi punti le due curve condividono la medesima tangente ossia risultano mutuamente tangenti.
Comunque prima di determinare questi punti applichiamo quanto discusso nel caso della parabola ossia il metodo che, a partire dall'equazione implicita della famiglia di curve tangenti, permette di dedurre l'equazione dell'inviluppo.
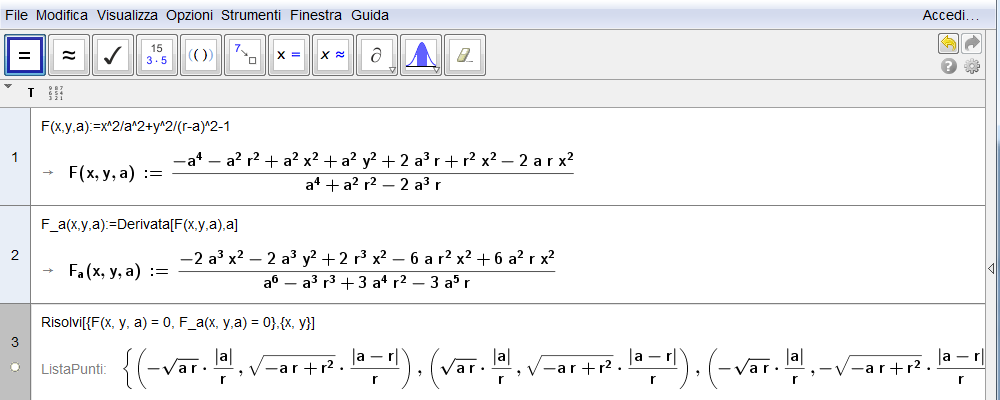
Sia quindi \(a\) la lunghezza di un semiasse per cui l'altro sarà espresso da \(r-a\). Ne segue che l'equazione canonica della famiglia di ellissi è \begin{equation}{x^2\over a^2}+{y^2\over (r-a)^2}=1\end{equation} e la funzione implicita associata è pertanto \begin{equation}F(x,y,a)={x^2\over a^2}+{y^2\over (r-a)^2}-1.\end{equation} Al variare di \(a\) nell'intervallo \([0,r]\) le equazioni \(F(x,y,a)=0\) rappresentano la famiglia di ellissi cercata ossia tali da avere costante, e pari a \(r\), la somma dei semiassi. Demandiamo ora il calcolo della derivata (parziale) prima di \(F(x,y,a)\) \begin{equation}F_a(x,y,a)={\partial F(x,y,a)\over \partial a},\end{equation} alle capacità simboliche di GeoGebra così come la ricerca delle soluzioni del sistema (di IV grado) che ne segue \begin{equation}\cases{F(x,y,a)=0\cr F_a(x,y,a)=0.\cr}\label{eq:29}\end{equation}
Figura 3.4. astroide04.ggb.
I risultati sono rappresentati in fig. 3.4: in particolare il sistema fornisce quattro punti disposti simmetricamente rispetto agli assi cartesiani. Considerando per esempio, il punto di coordinate \begin{equation}\cases{x={|a|\over r}\sqrt{a r}\cr\cr y={|a-r|\over r}\sqrt{r^2-a r},\cr}\label{eq:30}\end{equation} con le condizioni \(0< a< r\) e elevando al quadrato, la coppia di coordinate si può riscrivere come \begin{equation}\cases{x^2={a^3\over r}\cr y^2={(r-a)^3\over r}.\cr}\end{equation} Estratta la radice cubica \begin{equation}\cases{x^{2/3}={a\over\root 3\of{r}}\cr\cr y^{2/3}={r^{2/3}-{a\over\root 3\of{r}}}\cr}\end{equation} e sommando membro a membro, giungiamo alla \begin{equation}x^{2/3}+y^{2/3}=r^{2/3}\end{equation} che coincide con l'equazione implicita \eqref{eq:17} dell'astroide.
I punti comuni di tangenza sono evidentemente le soluzioni del sistema \eqref{eq:29}: le coordinate di quello appartenente al I quadrante, utilizzate nella figura 3.3, discendono immediatamente dalle \eqref{eq:30} e sono \begin{equation}\cases{x={a}\sqrt{a\over r}\cr y={(r-a)}\sqrt{1-{a\over r}}.\cr}\end{equation} Nella animazione di fig. 3.3 si tenga presente che al parametro a introdotto sopra corrisponde lo slider g.