Ellisse: costruzione n. 5
La costruzione qui proposta è molto semplice e costituisce il cosiddetto compasso ellittico.
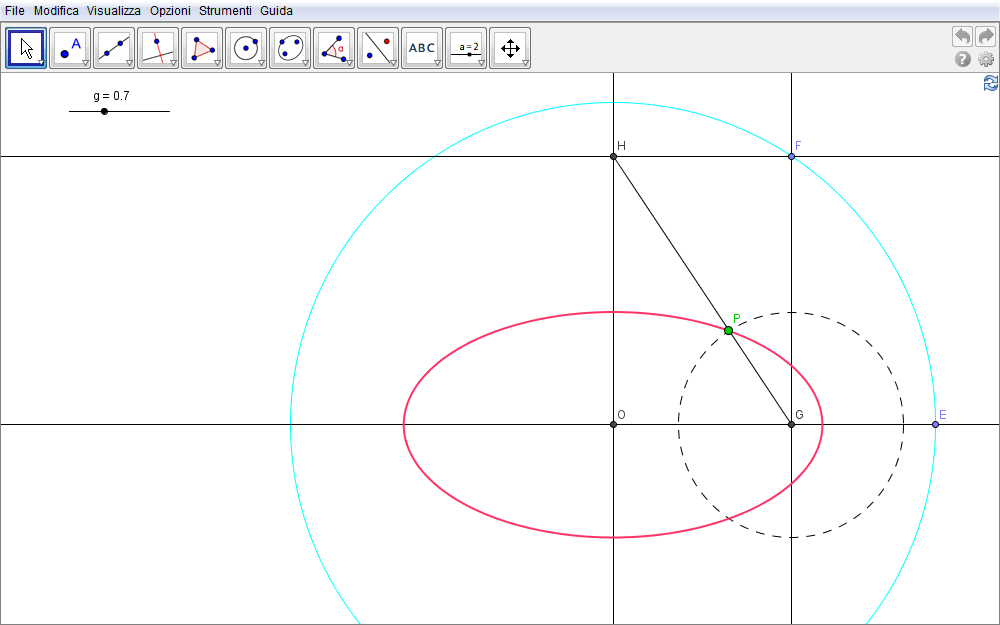
- Tracciate due rette ortogonali che si intersecano in O (asse x e asse y, fig. 2.13),
- si consideri su una di esse, per esempio quella orizzontale, il punto E e
- si tracci la circonferenza c con centro in O e come raggio il segmento OE.
- Se F è un punto qualsiasi della circonferenza stessa,
- tracciare per questo punto le rette parallele alle due rette iniziali
- e siano G e H i rispettivi punti di intersezione.
- Disegnato il segmento GH,
- definire uno slider avente per estremi lo zero e il raggio di c (in corrispondenza del valore massimo dell'intervallo si scrive raggio[c])
- Ora con lo strumento Circonferenza-dati centro e raggio
 si traccia la circonferenza di centro G e raggio pari allo slider.
si traccia la circonferenza di centro G e raggio pari allo slider. - Detto P il punto di intersezione tra questa circonferenza ed il segmento GH,
- il luogo di P al variare di F sulla circonferenza c è l'ellisse cercata.
Questa ha come semiassi le lunghezze dei segmenti PG e PH. Evidentemente in tale costruzione la lunghezza del segmento GH, che per costruzione è pari al raggio OF della circonferenza, esprime la somma dei due semiassi dell'ellisse.
Figura 2.13. ellisse13.ggb.
Dimostrazione
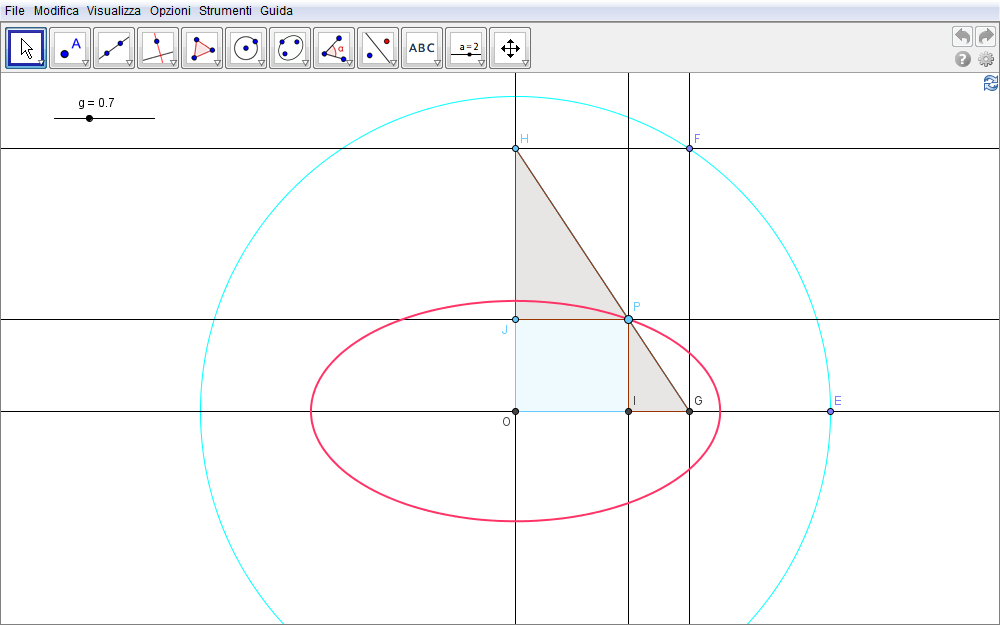
La dimostrazione fa uso di nozioni geometriche elementari e giunge ad ottenere l'equazione del luogo dei punti P. Difatti, supponendo che il punto P divida GH in due parti di lunghezza \(PH=a\) e \(PG=b\), risulta \(GH=a+b\). Per il teorema di Pitagora è quindi \begin{equation}OG^2+OH^2=(a+b)^2.\label{eq:1}\end{equation}
Figura 2.14. ellisse14.ggb.
Definite le proiezioni di P sulle rette ortogonali come I e J (fig. 2.14), la similitudine dei triangoli OGH e JPH permette di impostare la proporzione \begin{equation}{OG\over JP}={GH\over PH}\end{equation} da cui, tenendo conto che \(JP=x\) \begin{equation}OG={JP\cdot GH\over PH}={x(a+b)\over a}.\end{equation} Allo stesso modo, dalla similitudine dei triangoli OGH e IGP discende \begin{equation}{OH\over IP}={GH\over PG}\end{equation} e poiché \(IP=y\) \begin{equation}OH={IP\cdot GH\over PG}={y(a+b)\over b}.\end{equation} Inseriti tali valori nella relazione \eqref{eq:1} si ottiene \begin{equation}{x^2(a+b)^2\over a^2}+{y^2(a+b)^2\over b^2}=(a+b)^2\end{equation} che divisa per \((a+b)^2\) dà l'equazione aspettata dell'ellisse \begin{equation}{x^2\over a^2}+{y^2\over b^2}=1.\end{equation}
Osservazioni
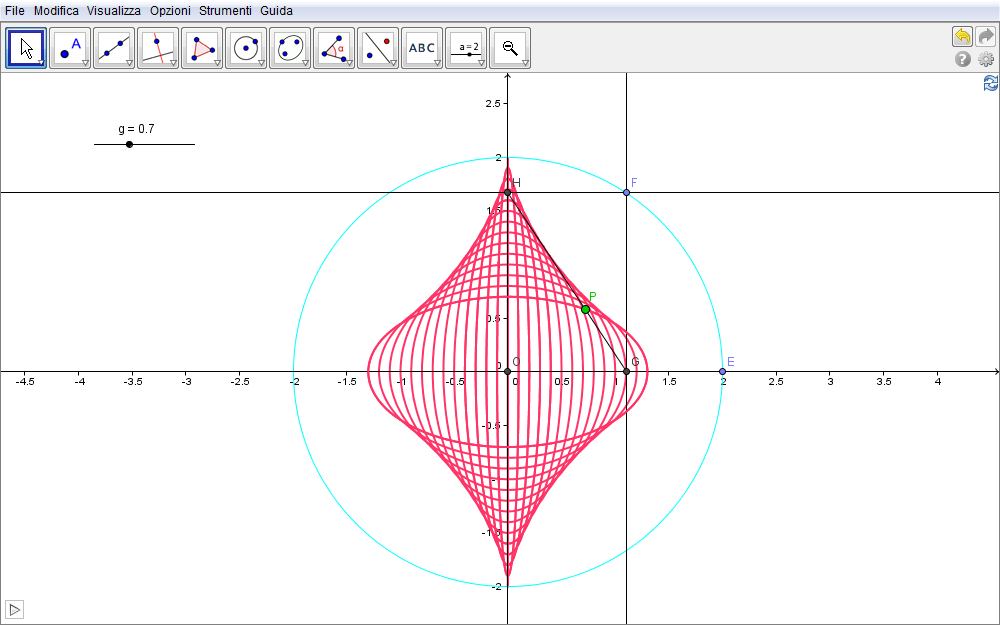
Nell'animazione seguente si tracciano le ellissi percorse da più punti del segmento GH così da far emergere visivamente una nuova curva particolarmente interessante, detta astroide o asteroide: questa, come vedremo, costituisce l'inviluppo generato da una famiglia di ellissi tali da avere costante la somma dei semiassi.
Figura 2.15. ellisse15.ggb.
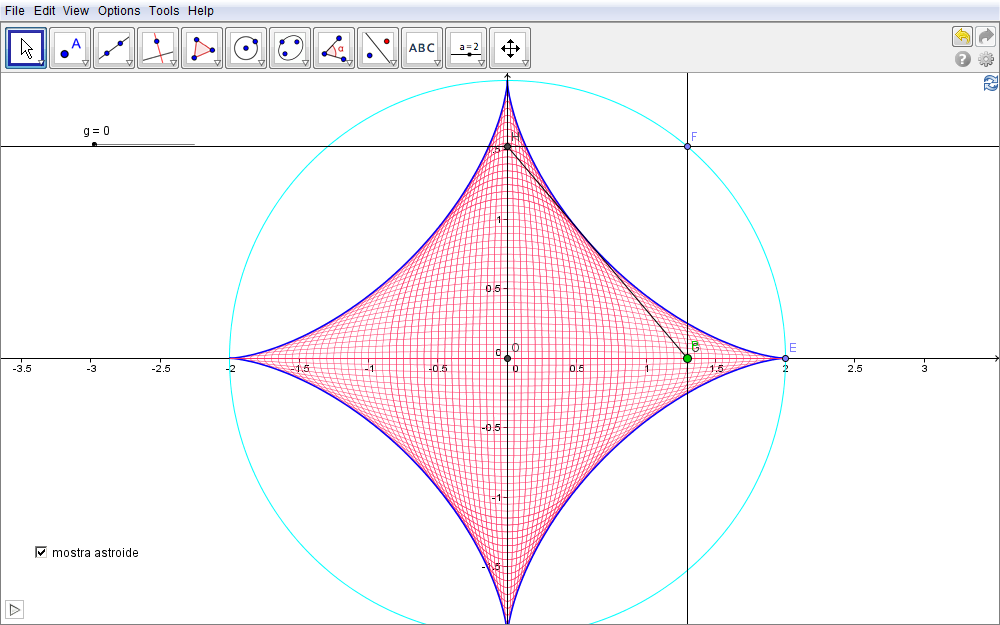
Infine, attivata l'animazione con un clic sull'icona in basso a sinistra, la figura 2.16 mostra in modo più preciso l'emergere dell'astroide: per evidenziarlo selezionare mostra astroide. Fermata l'animazione, si noti come, al variare del punto F (è sufficiente trascinarlo), il segmento GH sia sempre tangente a tale curva.
Figura 2.16. ellisse16.ggb.