Lisp »Tips 'n Tricks
»Simmetrie »1 »2 »3 »4 »5 »6 »7
TRAP2
;|
TRAP2.LSP
(C) 2005 by Claudio Piccini.
www.cg-cad.com
Lisp per disegnare tassellature
Traduzione in autolisp dell'algoritmo 'Egg Tile Generator'
in 'Computers, Pattern, Chaos and Beauty' di C.A. Pickover
2001, Dover Publications, Inc.
(* PseudoCode 13.1 *)
do i = 1 to res; (* loop in x direction *)
do j = 1 to res; (* loop in y direction *)
x = beta1+(gamma*i); (* compute x *)
y = beta2+(gamma*j); (* compute y *)
z = alpha*(sin(x)+sin(y)); (* compute z *)
c = trunc(z); (* convert z to an integer *)
if mod(c,modf) = 0 (* if c evenly divisible by modf *)
then PlotDot(i,j); (* plot a point at position (i,j) *)
end; (* end j loop *)
end; (* end i loop *)
|;
(defun c:trap2 ( / snapp
dim beta1 beta2 gamma alpha
i j x y z c
)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(initget (+ 2 4)) ; non 0, non negativo
(setq dim (getreal "\nDim? [100] "))
(if (= dim nil)(setq dim 100))
; beta1
(setq beta1 (getint "\nBeta1? [-11] "))
(if (= beta1 nil)(setq beta1 -11))
; beta2
(setq beta2 (getint "\nBeta2? [-12] "))
(if (= beta2 nil)(setq beta2 -12))
; gamma
(setq gamma (getint "\nGamma? [60] "))
(if (= gamma nil)(setq gamma 60))
; Alpha
(setq alpha (getint "\nAlpha? [10] "))
(if (= alpha nil)(setq alpha 10))
(setq i 1)
(while (<= i dim)
(setq j 1)
(while (<= j dim)
(setq x (+ beta1 (* gamma i)))
(setq y (+ beta2 (* gamma j)))
(setq z (* alpha (+ (sin x)(sin y))))
(setq c (fix z))
(if (= (rem c 3) 0)
(command "_point" (list i j))
)
(setq j (1+ j))
)
(setq i (1+ i))
)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
Test del lisp
Command: trap2
Dim? [100] Invio
Beta1? [-11] Invio
Beta2? [-12] Invio
Gamma? [60] Invio
Alpha? [10] Invio

Command: trap2
Dim? [100] Invio
Beta1? [-11] -16
Beta2? [-12] -21
Gamma? [60] 200
Alpha? [10] 4
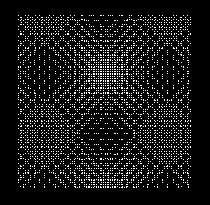
Command: trap2
Dim? [100] Invio
Beta1? [-11] 10
Beta2? [-12] 3
Gamma? [60] 25
Alpha? [10] Invio

Command: trap2
Dim? [100] Invio
Beta1? [-11] Invio
Beta2? [-12] 10
Gamma? [60] 50
Alpha? [10] Invio

Analisi del lisp
(setq c (fix z))
Questi esempi di tassellature sono ottenuti dalla sviluppo della formula z = alpha*(sin(x)+sin(y)), con z ridotto a numero intero non arrotondato.
La funzione in autolisp per convertire un numero reale in un numero intero è (fix n).
Fix restituisce un valore intero dal numero reale n troncando la parte decimale, ad esempio: (fix 3.5) ->3
Invece per arrotondare un numero reale si usano insieme due funzioni di autolisp: rtos e atoi.
(rtos numero modo accuratezza) restituisce una stringa dalla conversione di un numero, modo e accuratezza sono argomenti opzionali e servono per controllare il formato della stringa.
I modi sono 1=scientifico, 2=decimale, 3=ing., 4=arch., 5=frazionario. Esempi:
(rtos 2.123456 2 6)
"2.123456"
(rtos 2.123456 2 3)
"2.123"
(rtos 2.123456 2 0)
"2"
(atoi stringa) restituisce un numero intero dalla conversione di una stringa, la parte decimale viene scartata. Ad esempio (atoi "2.999") ->2.
Quindi per arrotondare un numero reale si scrive (atoi (rtos numero 2 0)). Esempi:
(atoi (rtos 0.89 2 0))
1
(atoi (rtos 0.45 2 0))
0
cioè (atoi (rtos 2.51 2 0)) è 3, mentre (fix 2.51) è 2.
(if (= (rem c 3) 0)(command "_point" (list i j)))
Se il resto è 0 allora il lisp disegna un punto.
In Autolisp la funzione da usare in questo caso è (rem n1 n2 n3 ...) che restituisce il resto della divisione tra il primo numero n1 ed il prodotto dei numeri rimanenti.
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 8 Aprile 2005
|





