Lisp »Tips 'n Tricks
»Automi »1 »2 »3
Automi cellulari a una dimensione (1)
Il Gioco della Vita è un esempio di automa cellulare. Il tipo più semplice di automa cellulare è quello a una dimensione.
AC1 disegna dall'alto verso il basso l'evoluzione di n automi cellulari a una dimensione nel corso di x generazioni, sotto forma di una serie di righe formate da punti casuali.
Ogni automa è condizionato dalla presenza (o assenza) di automi nelle 2 celle vicine a destra e a sinistra. Ogni cella ha valore 1 o 0. Si somma il contenuto della cella in esame con il contenuto delle 2 celle a destra e delle 2 celle a sinistra e si procede secondo la regola:
Un esempio con 5 automi:
Command: ac1
Numero automi? 5
Iterazioni? 5
Generazione 0=(1 1 0 1 1)
4 4 4 4 4
Generazione 1=(1 1 1 1 1)
5 5 5 5 5
Generazione 2=(0 0 0 0 0)
0 0 0 0 0
Generazione 3=(0 0 0 0 0)
0 0 0 0 0
Generazione 4=(0 0 0 0 0)
0 0 0 0 0
Generazione 5=(0 0 0 0 0)
Come per il lisp precedente il problema delle celle di confine è risolto immaginando il nastro di celle come se fosse un anello:
A B C D E
la somma di A=A+BCED
la somma di B=B+CDEA
la somma di C=C+DEBA
la somma di D=D+EACB
la somma di E=E+ABDC
;|
AC1.lsp (C) 2004 by Claudio Piccini.
1 Maggio 2004 (versione 1.1)
www.cg-cad.com
Il Gioco della Vita a una dimensione
|;
;|
Genera un numero casuale da 0 a 100.
Il seme e' inizializzato con la variabile DATE
in questo modo la serie di numeri casuali
e' diversa per ogni sessione del gioco.
|;
(defun rn ( / m b c)
(if (not sd) (setq sd (getvar "DATE")))
(setq m 65521 b 15937 c 33503 sd
(rem (+ (* b sd) c) m)
)
(setq sd (* (/ sd m) 101))
)
;|
trasforma il numero casuale
(0.0,100.0)->(0,1)
|;
(defun rand ( / sx)
(setq sx (rn))
(if (<= (fix sx) 50)
(setq sx 0)
(setq sx 1)
)
)
;|
inizializza la lista lnc con
valori casuali 0,1
|;
(defun go_life (na / i)
(setq i 0)
(while (< i na)
(setq lnc (append lnc (list (rand))))
(setq i (1+ i))
)
(setq lnc lnc)
)
;|
(contaVicini) conta i vicini di e
Restituisce la somma
somma = e+(e-2)+(e-1)+(e+1)+(e+2)
|;
(defun contaVicini (n L lung / somma)
(setq somma 0)
;|
controlla se il valore di n-2 e n+2
oltrepassa i limiti della lista L
|;
(if (and (>= (- n 2) 0)(< (+ n 2) lung))
(progn
(setq somma (+
(nth n L)
(nth (- n 2) L)
(nth (- n 1) L)
(nth (+ n 1) L)
(nth (+ n 2) L)
)
)
)
(progn
(cond
((= n 0)
(setq somma (+
(nth 0 L)
(nth 1 L)
(nth 2 L)
(nth (- lung 1) L)
(nth (- lung 2) L)
)
)
)
((= n 1)
(setq somma (+
(nth 1 L)
(nth 0 L)
(nth (- lung 1) L)
(nth 2 L)
(nth 3 L)
)
)
)
((= n (- lung 1))
(setq somma (+
(nth n L)
(nth (- n 1) L)
(nth (- n 2) L)
(nth 0 L)
(nth 1 L)
)
)
)
((= n (- lung 2))
(setq somma (+
(nth n L)
(nth (+ n 1) L)
(nth 0 L)
(nth (- n 1) L)
(nth (- n 2) L)
;| bug (ver 1.0)
(nth 1 L)
(nth 2 L)
|;
)
)
)
)
)
)
(setq somma somma)
)
(defun disegna_gen (lnc y / x )
(setq x 0)
(while (< x (length lnc))
(if (= (nth x lnc) 1)
(command "_point" (list x y))
)
(setq x (1+ x))
)
)
(defun c:ac1 ( / snapp sd
na itera i j y
lnc lnc2 lung_lista
)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(while
(progn
(setq na (getint "\nNumero automi? "))
(if (> na 4) nil T)
)
)
(initget (+ 1 2 4))
(setq itera (getint "\nIterazioni? "))
; inizializza la lista lnc
; con numeri casuali: 0,1
(setq lnc (go_life na))
(princ "\nGenerazione 0 ")
; (princ lnc)
(disegna_gen lnc 0)
(setq lung_lista (length lnc))
(setq i 1)
(setq y -1)
(while (<= i itera)
(setq j 0)
(while (< j lung_lista)
(setq somma (contaVicini j lnc lung_lista))
; (princ somma)(princ " ")
(cond
((= somma 0)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 1)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 2)
(setq lnc2 (append lnc2 (list 1)))
)
((= somma 3)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 4)
(setq lnc2 (append lnc2 (list 1)))
)
((= somma 5)
(setq lnc2 (append lnc2 (list 0)))
)
)
(setq j (1+ j))
)
(princ "\nGenerazione ")
(princ i)
;|
(princ "=")
(princ lnc2)
|;
(setq lnc lnc2)
(setq lnc2 nil)
(disegna_gen lnc y)
(setq y (1- y))
(setq i (1+ i))
)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
Test del lisp
Command: ac1
Numero automi? 600
Iterazioni? 400
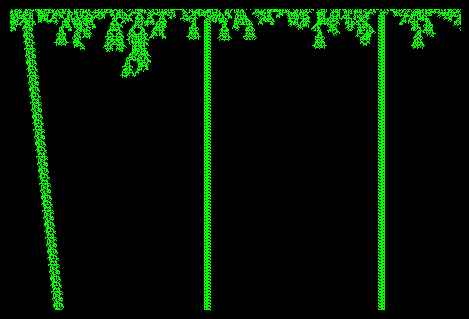
...
(cond
((= somma 0)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 1)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 2)
(setq lnc2 (append lnc2 (list 1)))
)
((= somma 3)
(setq lnc2 (append lnc2 (list 1)))
)
((= somma 4)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 5)
(setq lnc2 (append lnc2 (list 0)))
)
)
...
|
Test del lisp
Command: ac1
Numero automi? 600
Iterazioni? 300

...
(cond
((= somma 0)
(setq lnc2 (append lnc2 (list 1)))
)
((= somma 1)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 2)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 3)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 4)
(setq lnc2 (append lnc2 (list 0)))
)
((= somma 5)
(setq lnc2 (append lnc2 (list 1)))
)
)
...
|
Command: ac1
Numero automi? 300
Iterazioni? 100

Command: ac1
Numero automi? 300
Iterazioni? 100

Per approfondire:
I. Peterson, Il Turista Matematico, (cap.7 "Storie di vita"). Editore Sansoni (1998)
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 1 Maggio 2004
|





