 |
Lisp »Tips 'n Tricks
»Automi »1 »2 »3
Life
Il gioco ("Game of Life", modello di J.H. Conway, 1970) simula l’evoluzione di una popolazione, in termini di nascita e morte di singole entità (nel nostro caso punti bidimensionali).
Le condizioni che incidono circa la nascita e la morte sono la quantità di elementi adiacenti che generano uno stato di solitudine o di sovraffollamento. Ogni elemento vive e muore all'interno di una cella quadrata; l'insieme delle celle formano una mappa di N righe e M colonne (nel lisp N=M).
Le Regole del Gioco
Ogni cella è un automa a due stati, accesa o spenta, viva o morta, e risente dello stato di ogni cella del proprio intorno in modo tale che:
- se una cella ospita un automa vivo, questo continuerà a vivere anche nella generazione successiva solo se 2 o 3 delle otto celle ospitano automi vivi;
- se una cella vuota ha tre automi adiacenti vivi, allora ospiterà un nuovo automa;
- se un automa ha meno di 2 automi adiacenti vivi o più di 3 vivi, esso morirà per inedia o sovrappopolazione.
Le regole del Gioco sono tradotte nel seguente algoritmo:
- un punto V che ha due o tre vicini V con l'iterazione successiva resta V;
- un punto F diventa V con l'iterazione successiva se ha tre vicini V;
- un punto V che non ha nessun vicino V o ne ha al massimo solo uno con l'iterazione successiva diventa F;
- un punto V che ha quattro o più vicini V con l'iterazione successiva diventa F;
- tutte le V e le F prendono posto esattamente nello stesso istante: i punti prossimi-F non possono partecipare alla prossima-V di altri punti e i punti prossimi-V non possono partecipare alla prossima-F di altri punti.
Il punto 5 dell'algoritmo vuol dire che le liste devono essere 2.
Come primo passo si inizializza una lista di n elementi; ogni elemento della lista è una lista che contiene una chiave di ricerca, due numeri (le coordinate x e y del punto, l'entità che vive nella cella) e un valore di verità (F per falso, V per vero).
Come secondo passo si deve cambiare il valore di verità di alcune liste della mappa, da F (falso) a V (vero) in modo casuale; cioè alla domanda "c'è vita?" in alcuni casi si risponde sì e si scrive V per vero.
Con gli array l'implementazione dell'algoritmo è facile, ma visto che AutoLISP non gli usa come si contano i vicini in una lista?
Consideriamo una lista L di 9 elementi e ogni elemento di L è una lista e (numero numero lettera), quindi scriviamo la lista L come se fosse una matrice:
(
(0 0 "F")(0 1 "F")(0 2 "V")
(1 0 "V")(1 1 "F")(1 2 "F")
(2 0 "F")(2 1 "V")(2 2 "F")
)
Con la funzione (nth i L) e con l'aiuto di (while) possiamo scorrere tutta la lista e leggere tutti gli elementi e, e con le funzioni (car) estrarre le coordinate del punto (x,y) e il valore di verità (F,V).
Ogni elemento e si guarda intorno e se l'elemento, come ad esempio (0 0 "F"), è sul confine del campo la ricerca dei vicini può causare errori e di questo si deve tenere conto.
| (-? -? ?) | (-? ? ?) | (-? +? ?) |
| (? -? ?) | (0 0 "F") | (0 1 "F") |
| (+? -? ?) | (1 0 "V") | (1 1 "F") |
Questo è lo schema della ricerca di V,F:
| colonna-1 | colonna | colonna+1 |
| riga-1 | * | * | * |
| riga | * | (x,y,c) | * |
| riga+1 | * | * | * |
Cercare di individuare le liste in base alle coordinate x,y del punto non è pratico; la funzione (assoc e L) permette di individuare una lista (contenuta in una lista) con precisione, è necessario però inserire all'interno di ogni e una chiave di ricerca (che può essere un numero o una parola o una combinazione alfanumerica), nel nostro caso sarà un valore numerico (incrementabile in modo automatico) sufficentemente alto, per non confonderlo con le coordinate del punto, ad esempio 1000.
Una soluzione per i punti di confine è contare i valori di verità (F,V), salvare il risultato in una variabile contatore (conta_fv) e ignorare i punti con conta_fv<8. Nell'esempio il punto (1 1) è circondato da 8 punti di confine che non cambiano di stato ma contribuiscono al cambiamento di stato di (1 1).
|
1000
F
(x,y)=(0 0)
|
1001
F
(x,y)=(0 1)
|
1002
V
(x,y)=(0 2)
|
|
1003
V
(x,y)=(1 0)
|
1004
F
(x,y)=(1 1)
|
1005
F
(x,y)=(1 2)
|
|
1006
F
(x,y)=(2 0)
|
1007
V
(x,y)=(2 1)
|
1008
F
(x,y)=(2 2)
|
- Test: stampa il numero di vicini V per ogni punto di una mappa 8x8 - esclusi i punti di confine a Nord e a Sud.
Il terzo passo consiste nello scrivere il codice delle regole, facendo attenzione al punto 5.
- Test: mostra l'evoluzione del campo di gioco dalla generazione 0 alla generazione 1.
E infine l'ultimo passo consiste nello scrivere una procedura per disegnare i punti in autocad, ad esempio come centri di cerchi di raggio=0.5 e inserire un'istruzione while che chiede al giocatore se vuole continuare a giocare.
;|
LF.lsp (C) 2004 by Claudio Piccini.
27 Aprile 2004 (versione 1.0)
www.cg-cad.com
Il Gioco della Vita
(The Game of Life di J.H. Conway)
|;
;|
estrae un numero casuale
da 0 a 63
Il seme e' inizializzato con la variabile DATE
in questo modo la serie di numeri casuali
e' diversa in ogni sessione di gioco.
|;
(defun rn ( / m b c)
(if (not sd) (setq sd (getvar "DATE")))
(setq m 65521 b 15937 c 33503 sd
(rem (+ (* b sd) c) m)
)
(setq sd (* (/ sd m) 64))
)
;|
inizializza la mappa
come una griglia di punti MxN = 8x8
memorizzati in liste di associazioni:
(chiave x y valore_verita'="F")
|;
(defun go_life (mXn / key)
(setq key 1000)
(while (<= M mXn)
(setq N 0)
(while (<= N mXn)
(setq mappa (append mappa
(list (list key M N "F"))
)
)
(setq key (1+ key))
(setq N (1+ N))
)
(setq M (1+ M))
)
(setq mappa mappa)
)
;|
inserisce punti "V" nella mappa
in modo casuale
|;
(defun random_life (mappa mXn /
z i k key x y
cellaF cellaV
)
(setq z 25) ; numero punti "V"
(setq i 0)
(while (< i z)
(setq k (fix (rn)))
(setq key (+ 1000 k))
(setq cellaF (assoc key mappa))
(setq x (cadr cellaF))
(setq y (caddr cellaF))
(setq cellaV (list key x y "V"))
(setq mappa (subst cellaV cellaF mappa))
(setq i (1+ i))
)
(setq mappa mappa)
)
;|
contaVicini conta i "V"
esclude dalla conta i punti di confine
della mappa a Nord e a Sud:
la mappa puo' essere vista come un
cilindro aperto sul piano.
|;
(defun contaVicini (e L / key conta_fv conta_V)
(setq key (car e))
(setq conta_fv 0)
(setq conta_V 0) ;conta i "V"
(if (assoc (- key 9) L)
(progn
(if (= (cadddr (assoc (- key 9) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (- key 8) L)
(progn
(if (= (cadddr (assoc (- key 8) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (- key 7) L)
(progn
(if (= (cadddr (assoc (- key 7) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (- key 1) L)
(progn
(if (= (cadddr (assoc (- key 1) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (+ key 1) L)
(progn
(if (= (cadddr (assoc (+ key 1) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (+ key 7) L)
(progn
(if (= (cadddr (assoc (+ key 7) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (+ key 8) L)
(progn
(if (= (cadddr (assoc (+ key 8) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (assoc (+ key 9) L)
(progn
(if (= (cadddr (assoc (+ key 9) L)) "V")
(setq conta_V (1+ conta_V))
)
(setq conta_fv (1+ conta_fv))
)
)
(if (= conta_fv 8)
(setq conta_V conta_V)
(setq conta_V -1)
)
)
;|
Disegna n cerchi
con centro in (chiave M N "V")
|;
(defun disegna_mappa (mappa / i x y valore)
(setq i 0)
(while (< i (length mappa))
(setq x (cadr (nth i mappa))) ; coordinata X del punto
(setq y (caddr (nth i mappa))) ; coordinata Y del punto
(setq valore (cadddr (nth i mappa))) ; valore V,F
(if (= valore "V")
(progn
(command "_circle" (list x y) 0.5)
(setq ent (append ent (list (entlast))))
)
)
(setq i (1+ i))
)
(setq ent ent)
)
(defun c:lf ( / snapp sd M N mXn risp ent
mappa mappa2 i j conta
key x y valore mappa2 lista
)
(setvar "cmdecho" 0)
(setq snapp (getvar "osmode"))
(command "_osnap" "_non")
(setq M 0 N 0 mXn 7)
; inizializza la mappa
(setq mappa (go_life mXn))
; inserisce casualmente punti V
(setq mappa (random_life mappa mXn))
;|
legge la lista mappa e salva la nuova
configurazione in mappa2
|;
(while
(progn
(setq i 0)
(while (< i (length mappa))
(setq conta
(contaVicini (nth i mappa) mappa)
)
(setq key (car (nth i mappa))) ; chiave di ricerca
(setq x (cadr (nth i mappa))) ; coordinata X del punto
(setq y (caddr (nth i mappa))) ; coordinata Y del punto
(setq valore (cadddr (nth i mappa))) ; valore V,F
(cond
((= conta -1) ; punto di confine
(setq lista (list key x y valore))
(setq mappa2 (append mappa2 (list lista)))
)
((= conta 0) ; se V allora diventa F
(setq lista (list key x y "F"))
(setq mappa2 (append mappa2 (list lista)))
)
((= conta 1) ; se V allora diventa F
(setq lista (list key x y "F"))
(setq mappa2 (append mappa2 (list lista)))
)
((= conta 2) ; il valore resta immutato
(setq lista (list key x y valore))
(setq mappa2 (append mappa2 (list lista)))
)
((= conta 3) ; se V resta V, se F diventa V
(setq lista (list key x y "V"))
(setq mappa2 (append mappa2 (list lista)))
)
((>= conta 4) ; se V diventa F
(setq lista (list key x y "F"))
(setq mappa2 (append mappa2 (list lista)))
)
)
(setq i (1+ i))
)
(setq mappa mappa2)
(setq mappa2 nil)
(setq ent (disegna_mappa mappa))
(initget "S s N n")
(setq risp
(getkword "\nNuova generazione? (S/N) [s]: ")
)
(cond
((or (= risp "N")(= risp "n"))
nil
)
((or (= risp "S")(= risp "s")(= risp nil))
(if (/= ent nil)
(progn
(setq j 0)
(while (< j (length ent))
(entdel (nth j ent))
(setq j (1+ j))
)
(setq ent nil)
)
)
T
)
)
)
)
(setvar "osmode" snapp)
(command "_redraw")
(setvar "cmdecho" 1)
(princ)
)
;;;eof
|
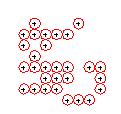 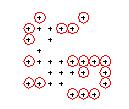 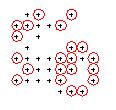 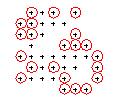 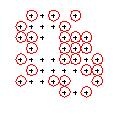
Con questa modifica al lisp la vita diventa più difficile:
...
(cond
((= conta -1) ; se punto di confine allora F
(setq lista (list key x y "F"))
(setq mappa2 (append mappa2 (list lista)))
)
...
 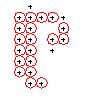 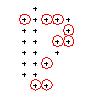 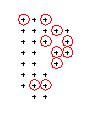  
Per approfondire:
Life... il gioco della vita di Conway
Il gioco della vita: algoritmo
Lisp »Tips 'n Tricks
Ultimo Aggiornamento_Last Update: 27 Aprile 2004
|
 |

