| Circonferenza goniometrica (r = 1) | Archi orientati |
|
|
| Quadranti della Circonferenza goniometrica | Distanza fra due punti |
|
|
d2 = x02 + y02 |
Lezione del 28/3/2001
Trigonometria
Cerchio goniometrico
| Circonferenza goniometrica (r = 1) | Archi orientati |
|
|
| Quadranti della Circonferenza goniometrica | Distanza fra due punti |
|
|
d2 = x02 + y02 |
Misura in radianti
Nel cerchio goniometrico (r = 1) la lunghezza della semicirconferenza è uguale a p
L'angolo corrispondente misura 180°
Si può mettere in corrispondenza l'arco di circonferenza con l'angolo relativo
Vale la relazione: arco = angolo * p / 180
Gli archi si misurano in radianti
Funzioni goniometriche
| Seno | Sinusoide |
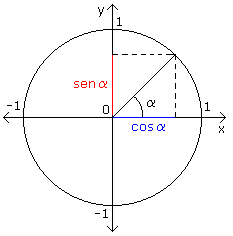 |
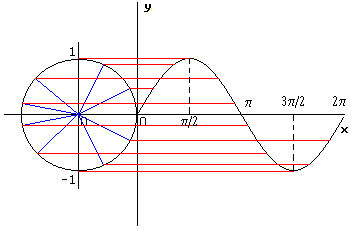 |
| E' facile vedere che: sen 0° = 0 |
|
| Coseno | Cosinusoide |
|
|
| E' facile vedere che: cos 0° = 1 |
|
| Tangente | Tangentoide |
|
|
tg a = sen a / cos a |
Nel cerchio goniometrico, per definizione, vale sempre la relazione: sin2x + cos2x = 1
Fase di una sinusoide
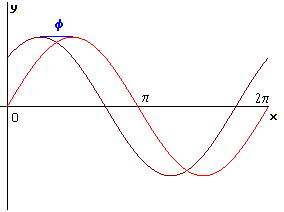 |
f è lo spostamento di fase della generica sinusoide rispetto a quella disegnata in rosso che, invece, è la sinusoide con fase 0 |
|
Sinusoide con fase a 45° (y = sen(x + p/4)) |
|
Sinusoide con fase a 90° (y = sen(x + p/2)) Viene detta in quadratura di fase Notare che è identica alla cosinusoide |
|
Sinusoide con fase a 180° (y = sen(x + p)) Viene detta in opposizione di fase |
|
Sinusoide con fase a 270° (y = sen(x + 3p/2)) |
Periodicità delle funzioni goniometriche
L'andamento, ad esempio, della sinusoide si ripete quando il punto ha percorso un giro completo del cerchio
Si dice, in questo caso, che la sinusoide è periodica di periodo 2p
La velocità con cui un punto percorre la circonferenza è in relazione diretta con la frequenza (cioè il numero di volte che il punto percorre un'intera circonferenza nell'unità di tempo)
In particolare, la velocità angolare (che si indica con w) è l'arco percorso nell'unità di tempo e si misura in rad / sec
La relazione, dunque, tra la frequenza f e w è w = 2pf
Coordinate polari e cerchio generico
| Cerchio generico e funzioni goniometriche | Coordinate polari di un punto |
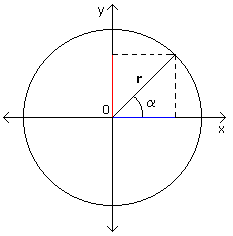 |
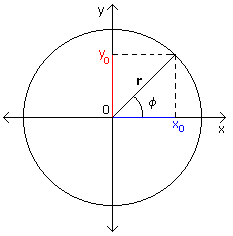 |
In questo caso cos a = x / r |
Modulo Fase |
Esercizi
- Convertire i seguenti angoli in radianti
- Trovare le seguenti formule di trasformazione
- Semplificare le seguenti espressioni
- Calcolare i valori delle rimanenti funzioni goniometriche, essendo dato:
- Discutere e disegnare il grafico della seguente espressione per diversi valori della frequenza e di A
Ho aggiunto, nella pagina della settimana scorsa, altri esercizi sui logaritmi
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia