D , y C , allora
l'applicazioneLezione del 21/3/2001
Funzioni
Una funzione, nel senso che comunemente si attribuisce alla parola, è una legge che associa a un valore di una variabile indipendente un valore di una variabile dipendente.
I valori di cui si parla sono, comunemente, numerici. Più precisamente, e sempre nell'accezione più comune, data una variabile x reale, detta indipendente, e una variabile y reale, detta dipendente, allora possiamo scrivere
y = f(x)
dove f( ) (o solo f) rappresenta la legge che associa y a x (x, in questo caso, può anche essere chiamato argomento); ad esempio
In maniera più rigorosa e generale, una funzione
può essere definita come un'applicazione tra
insiemi numerici; siano C e D
due insiemi numerici e x D , y C , allora
l'applicazione
corrisponde alla funzione y = f(x).
L'insieme D viene
chiamato dominio di esistenza (anche solo dominio)
ed è l'insieme di tutti i valori che la x può
prendere, mentre l'insieme C, detto anche codominio,
è l'insieme di tutti i valori possibili per la y. Ad
esempio la funzione y
= 1/x è definita per tutti i valori
che la x può prendere tranne che per x = 0
(per cui D = 
- {0} che si può anche scrivere come {x: x ¹ 0}); altro esempio:
il dominio della funzione sqrt(x) è {x: x ³ 0}
(sqrt indica la radice quadrata; dall'inglese SQuare RooT)
Se D,C 
e x D allora la f(x)
viene chiamata funzione reale di variabile reale
ed è il tipo più comune di funzione.
Se D 
e C e n D allora la funzione y = f(n) (che possiamo trovare scritta come y = fn o y =
xn ; n, in questo caso, è
detto anche indice) viene chiamata successione
o sequenza. Ad esempio quando viene registrato
su un calcolatore elettronico un segnale audio questo può essere
visto come una successione di numeri a causa del campionamento e
dell'acquisizione; in questo caso è possibile applicare il ricco
sistema di tecniche matematiche che va sotto il nome di Digital
Signal Processing (elaborazione numerica dei segnali)
Se D 
e C e x D allora la funzione y = f(x) viene detta funzione complessa di
variabile complessa o anche funzione analitica
oppure funzione olomorfa. Le funzioni olomorfe
sono molto importanti nella trattazione dell'analisi di
Fourier; quest'ultima è un insieme di tecniche matematiche
che permettono, ad esempio, di estrarre molte informazioni sulla
composizione armonica di un evento sonoro.
Data un'applicazione
se esiste un'applicazione
allora la funzione g( ) viene detta funzione inversa di f( ); in altre parole, sia y = f(x): allora x = g(y) è la sua funzione inversa.
Una funzione viene detta continua
intorno ad un valore x0 D
se, fissati i valori d,
e > 0 (d, e ) piccoli a piacere,
e se |x - x0| < d, allora
|f(x) - f(x0)| < e. In altre parole, una funzione è continua se una
piccola variazione della x non produce una
grande variazione della y o addirittura uno
"scatto" da un valore a un altro. Una funzione è
continua se è continua in tutti i suoi punti.
|
|
Funzione continua |
Funzione discontinua |
Le funzioni reali di variabile reale (d'ora in poi semplicemente funzioni) possono essere di due tipi
Una funzione algebrica è costituita da una quasiasi espressione contenente termini in x elevati a qualsiasi potenza intera o frazionaria; ad es.
Una funzione algebrica del tipo
y = anxn + an-1xn-1 + .... + a1x1 + a0x0
viene detta anche polinomio di grado n in x e indicata con Pn(x). I polinomi sono funzioni algebriche molto importanti e sono molto utili, ad es., nell'approssimazione di generiche funzioni.
La precedente espressione può anche essere scritta, in maniera più compatta, come
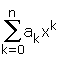
che si legge: sommatoria, per k cha va da 0 a n, di a con k per x alla k.
Una funzione trascendente non può, invece, essere espressa come una semplice combinanzione di potenze della x. Esempi di tale categoria di funzioni sono
La funzione y = ax è molto importante e gode di interessanti proprietà; qui sotto ne vediamo alcune
x }
, y > 0} (1)
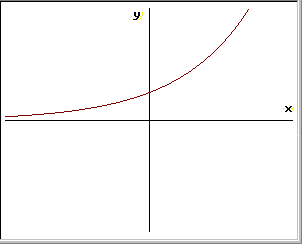
Funzione esponenziale
La funzione logaritmo è ancora più importante ed ha numerose applicazione nella scienza e nella tecnica; nel nostro caso, per fare un solo esempio, viene usato in Acustica per esprimere i livelli di pressione sonora rispetto un valore di riferimento: stiamo parlando del deciBel (dB), unità logaritmica di misura (relativa) per le ampiezze (non obbligatoriamente di grandezze acustiche).
Dato che la funzione logaritmo è stata definita come funzione inversa dell'esponenziale y = ax, possiamo definirla come
x = logay (leggasi logaritmo in base a di y)
cioè il logaritmo è l'esponente a cui bisogna elevare la base a per ottenere l'argomento y. Dalle proprietà della funzione esponenziale, abbiamo
, x > 0} (1)y
}
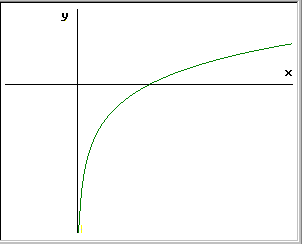
Funzione logaritmo
In matematica si usano solo alcune basi standard; queste sono:
il numero e detto numero di Nepero; e è un numero reale trascendente e vale 2.718.... ed è il più usato nella teoria. Un logaritmo in base e viene anche chiamato logaritmo naturale e si scrive: y = ln x (che sostituisce logex)
il numero 10, molto usato nelle applicazioni tecniche; ad esempio il deciBel è un'unità logaritmica in base 10. Il logaritmo in base 10 si scrive: y = logx (che sostituisce log10x)
il numero 2, molto usato in informatica. I logaritmi in questa base vengono chiamati anche duali e si scrivono: y = ld x (che sostituisce log2x).
E' comunque possibile esprimere qualsiasi logaritmo in qualsiasi base usando la formula di trasformazione
logax = ln x / ln a
nel caso in cui vogliamo rappresentarlo come logaritmo naturale
_______________________________
Nota 1: affermazione valida solo se a > 0
Nota 2: questa proprietà, e le seguenti, è valida se x,z > 0
- Determinare il dominio di esistenza delle seguenti funzioni
- Risolvere le seguenti espressioni discutendone il campo di validità
- Dimostrare la formula di trasformazione
- Svolgere i seguente esercizi
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia
