Mentire con le statistiche

Questo articolo completa alcune osservazioni
contenute nel testo originale
e nei commenti all’edizione italiana
di How to Lie with Statistics di Darrell Huff.

L’utilità dei numeri imprecisi

Giancarlo Livraghi – novembre 2008

Disponibile anche in pdf
(migliore come testo stampabile)

Si pensa, in generale, che un dato statistico sia tanto più utile e rilevante quanto più è preciso. Questa è spesso un’illusione, quando non è un inganno. Non è raro il caso che un numero dettagliato, magari con i decimali, dia una falsa percezione di esattezza.

Per esempio 10,52 può voler dire, in realtà, “pressappoco fra 9 e 12” (o, in molti casi, essere ancora meno preciso). Non solo a causa dell’intrinseca inesattezza di ogni studio basato su un “campione” (come è chiaramente spiegato nel libro di Darrell Huff e in ogni buon testo di statistica) ma anche per la natura sostanziale dei dati, il cui significato è spesso diverso da ciò che può sembrare a un osservatore disattento – o a chi, più o meno intenzionalmente, vuole usare i numeri per dare senso a un’osservazione arbitraria o strumentale. (Vedi Dare i numeri).

Qualcuno potrebbe osservare che in varie mie analisi (vedi la sezione dati) ci sono indici numerici più precisi di quanto in realtà possano essere significativi. Avrebbe ragione, se non ci fossero in quelle pagine osservazioni sulla non esattezza delle fonti. Il motivo per cui ci sono alcuni “dati con i decimali” è lontano da qualsiasi tentazione di “falsa certezza”. Al contrario, è un modo per segnalare che talvolta le differenze (in particolare quando si tratta di indici o percentuali) sono troppo piccole per poter essere rilevanti. Questo è uno dei motivi per cui molti confronti sono semplificati in grafici (mai manipolati nei modi che Darrell Huff spiega nei capitoli 5 e 6 del suo libro e che ho riassunto in Il morbo di powerpoint). Non si tratta solo di rendere facilmente percettibile il senso di un’analisi, ma anche di interpretare con semplice evidenza il fatto che i numeri non sono più precisi e attendibili di quanto risulta da una intenzionalmente approssimata percezione visiva.

Non si tratta solo di “dare una seconda occhiata”, come consiglia Huff, ma anche di avere un’idea chiara di che cosa un dato possa significare. Uno dei modi per capire meglio è “triangolare” l’informazione. Come si concilia una certa affermazione con ciò che sappiamo su quell’argomento o con altre e diverse analisi dello stesso tema? Non solo le coerenze, ma anche le discordanze, sono strumenti per capire meglio – o almeno per avere un dubbio, che può essere il punto di partenza per un utile cambiamento di prospettiva (vedi Errori di prospettiva, capitolo 21 di Il potere della stupidità).

Ma non sempre è un problema che i dati siano imprecisi. Ci sono concetti utili e validi nonostante il fatto che non hanno alcuna pretesa di esattezza numerica né significatività statistica.

Per esempio la Legge di Sturgeon “il novanta per cento di tutto è spazzatura” può essere espressa (come infatti accade) anche con altre percentuali. Che si dica 99 o 80 per cento non ne cambia il significato. Basta capire che “molta” spazzatura non è un motivo sufficiente per ignorare il fatto che c’è un uno o dieci o venti per cento di qualcosa che non lo è – e vale la pena di scoprirlo.

La proverbiale frase one percent inspiration, 99 percent perspiration non vuole necessariamente dire che si tratti di “sudore”. Afferma con chiarezza il fatto che un’intuizione può essere illuminante, ma non basta, ci vuole impegno perché produca risultati. È generalmente attribuita a scrittori e riferita a opere di letteratura o di arte, ma è interessante constatare che l’autore più probabile è Thomas Edison – e che comunque riguarda anche la scienza e la tecnologia. Ovviamente il numero è irrilevante, si tratta di un concetto e non di un dato statistico che sarebbe impossibile misurare. Ma la sua “assoluta incertezza” numerica non rende l’affermazione meno utile e interessante.

Può accadere che un criterio, inizialmente basato su un’ipotesi statistica, assuma significati più estesi, perdendo valore numerico, ma non per questo validità pratica. Per esempio il “principio di Pareto”, noto come tale in mezzo mondo, ebbe origine quando Vilfredo Pareto aveva rilevato, circa cent’anni fa, che l’80 % del reddito in Italia andava al 20 % della popolazione.

Che quelle percentuali fossero esatte è improbabile, che il fatto fosse vero è molto credibile. In epoche successive la situazione era migliorata (non solo in Italia) con una distribuzione meno squilibrata del reddito, mentre in anni recenti abbiamo avuto un arretramento (qualcuno assurdamente lo chiamava “progresso”) di cui stiamo constatando le perverse conseguenze sociali, umane, culturali ed economiche – con miope e tardiva stupidità.

Un fatto interessante, quanto desolante, è che un’analisi contenuta nel United Nations Development Program Report del 1992 indica, nel 1989 e su scala “globale”, una situazione molto simile a quella rilevata tanti anni prima da Pareto: l’83 % del reddito (“prodotto interno lordo”) nel mondo appare concentrato nel 20 % degli abitanti.

Ma il “principio di Pareto” ha avuto, e continua ad avere, anche altre e più estese applicazioni. Ha assunto il significato generico di “il venti per cento di qualcosa ha (o equivale a) l’ottanta per cento di qualcos’altro”. O viceversa. Dove ovviamente l’ipotetica esattezza aritmetica ha perso ogni significato (anche se è curioso constatare che in parecchi casi concreti il rapporto non è molto lontano da 20-80).

Non è questa la sede per entrare nelle complesse analisi statistiche basate sulla “distribuzione probabilistica di Pareto”, non solo in economia, ma anche in sociologia, biologia, logistica, geofisica e varie altre applicazioni scientifiche o tecniche. Come, per esempio, in questi istogrammi.

     

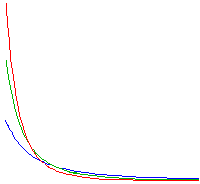
Queste elaborazioni si riferiscono al tema originale delle analisi di Pareto,
cioè alla distribuzione del reddito in un’economia “normale”
(diversa da quella patologica in cui stiamo vivendo).
Come già osservato, i criteri sono applicati anche ad altri generi di studi.
L’interpretazione dei grafici, nel loro specifico significato,
è tutt’altro argomento – ma è eloquente la loro semplicità.

Una delle applicazioni del “principio di Pareto” si trova nel marketing. È diventato un “modo di dire”, per esempio, che “il 20 per cento dei consumatori usa (o acquista) l’80 per cento del prodotto”. Oppure ci possono essere differenze stagionali, geografiche, demografiche, culturali eccetera – non sempre così ovvie come si possono immaginare. Può sembrare una generica banalità, ma spesso è vero (anche se non necessariamente in quella proporzione). E ovviamente se ne possono dedurre conseguenze pratiche. Per esempio concentrare le attività sulle persone più interessate – oppure cercare di allargare l’uso a categorie più ampie.

Questo, ovviamente, è solo uno di tanti esempi di come il concetto si può applicare, in modi diversi e in un’infinità di settori. Ed è, di fatto, applicato anche da chi non sa o non ricorda che si tratta del “principio di Pareto”.

Si possono fare ragionamenti analoghi anche su altri parametri, espressi come “princìpi” di vari autori o definiti in altri modi. Ci sono vari criteri utili (come ci sono molte idee sballate) che si esprimono in termini numerici senza avere verifica statistica o precisione matematica.

Insomma un concetto che non ha, o ha perduto, significato statistico può rimanere valido e concretamente utile. Basta sapere che cos’è e come funziona. E ovviamente evitare di trarne deduzioni o proiezioni numeriche troppo precise, da cui potrebbero derivare “false certezze” e perciò linee d’azione pericolosamente rigide o schematiche.

Con un’adeguata dose di buon senso (e con la sempre necessaria flessibilità nelle applicazioni pratiche) ci sono valutazioni “spannometriche” o “a lume di naso” che hanno un serio valore concreto e possono essere più utili di elaborazioni complesse in cui spesso si nascondono errori che diventano più insidiosi per la loro apparente “scientificità”.

home