Il paradosso di Achille e la Tartaruga

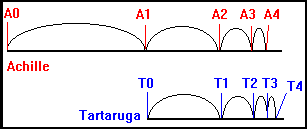Quando Achille si trova in Ao la tartaruga è in To. Achille corre per raggiungerla ed arriva in A1. La tartaruga nel frattempo si è spostata in T1, avendo percorso metà della distanza di Achille, ma restando sempre in vantaggio. Il processo si ripete, apparentemente fino all'infinito e sembra proprio che Achille non raggiunga mai la tartaruga. Svolgiamo però il calcolo delle distanze, cosi come dei tempi, supponendo che la velocità di Achille sia v =1 m/s e ricordando che la distanza AoA1 è di dieci metri. Achille percorre una distanza pari a Da = 10+5+2.5+... metri, in un tempo t = 10+5+2.5+... secondi. La tartaruga percorre una distanza Dt = 5+2.5+1.25+... metri in un tempo uguale. Si vede subito che si tratta di tre serie geometriche convergenti, p.es. Da = 10(1+1/2+1/4+...) = 10(1/(1-1/2)) = 10(2) = 20 metri. Dt è la metà di tale valore mentre il tempo impiegato è t = 10(1+1/2+1/4+...) = 10(1/(1-1/2)) = 10(2) = 20 secondi. Dunque dopo venti secondi, dopo aver percorso venti metri in tutto, Achille raggiunge la tartaruga e un attimo dopo la supera definitivamente. La vittoria dell'uno o dell'altra dipende da dove viene posto il traguardo. L'errore nel ragionamento è quello di ritenere che una somma di infiniti termini debba dare sempre un risultato infinito. Alla luce delle moderne conoscenze matematiche la soluzione è addirittura banale e si riduce ad un semplicissimo esercizio di cinematica.