Ritorna alla pagina di presentazione
Propagazione delle onde e principio di sovrapposizione
Lorenzo Roi (aprile 2009)
Propagazione
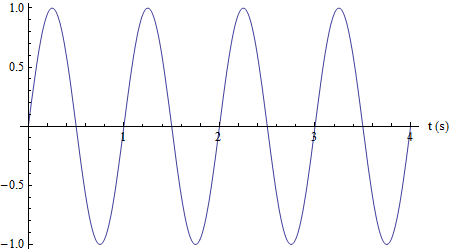
Grafico del moto armonico di un punto; l'ordinata rappresenta lo spostamento e in ascissa il tempo. È sostanzialmente la riproduzione di quanto si ottiene dall'oscilloscopio nel caso del suono di un diapason (in laboratorio, un La 440 Hz) oppure dalla registrazione dello stesso e la sua visualizzazione in un editor di files sonori (figura successiva).
La funzione tracciata possiede una pulsazione pari a 2π: ne segue che il periodo è pari ad T =1 s.

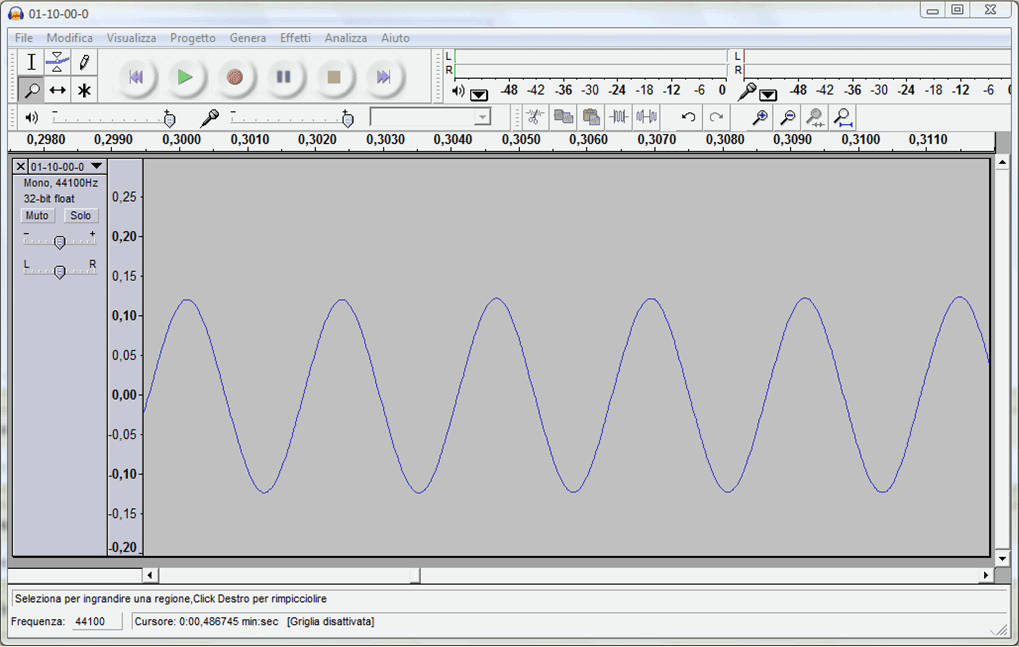
Registrazione sonora del suono emesso da un diapason di frequenza La 440 Hz.
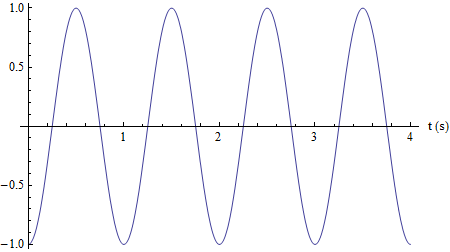
Il medesimo grafico con un angolo di fase pari a π/2: appare traslato verso destra di un quarto di periodo cioè di 0.25 s.
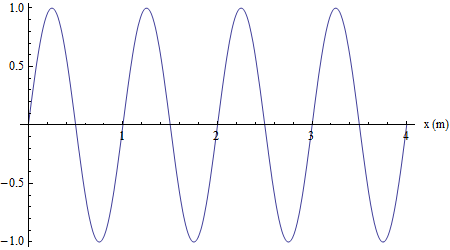
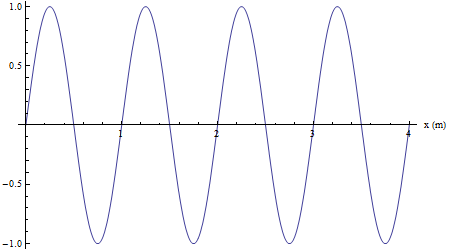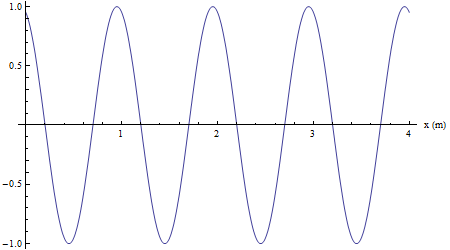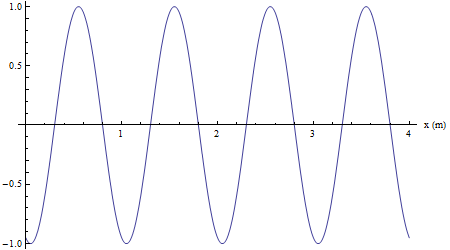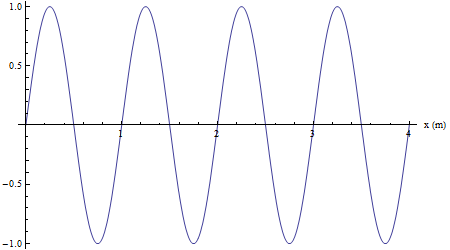
"Foto" di un'onda su una corda: questa volta in ordinata la grandezza fisica è lo spostamento da una posizione di equilibrio e in ascissa la distanza dalla "sorgente" (posta nell'origine). La periodicità spaziale è evidente ed è pari, in questa rappresentazione, alla lunghezza d'onda: λ=2π/2π=1 m.
Ancora sostanzialmente il medesimo grafico con aggiunto un angolo di fase pari a -![]() : si noti come la curva sia stata traslata verso destra (di quanti...metri?).
: si noti come la curva sia stata traslata verso destra (di quanti...metri?).
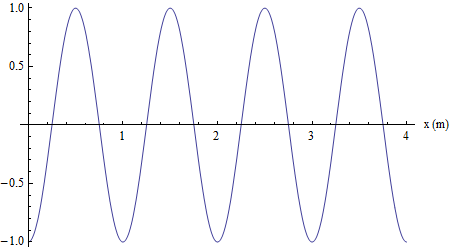
Costruiamo un'animazione dove si possa variare, nel tempo t, l'angolo di fase: in particolare, tale angolo assume valori via via crescenti e proporzionali a t. Ciò simula la successione di foto che si otterrebbero riprendendo, per esempio, una corda soggetta ad onde trasversali.
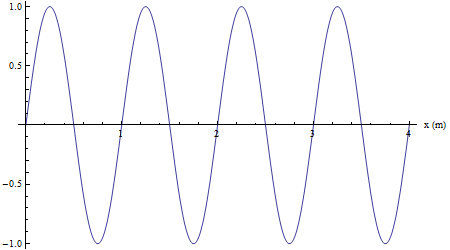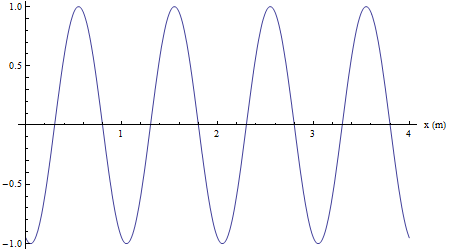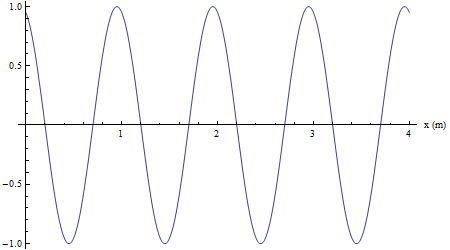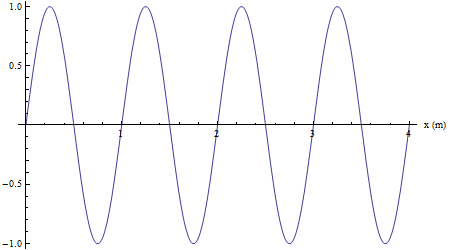
Nella successiva animazione si mette in evidenza il moto armonico della sorgente (punto rosso).
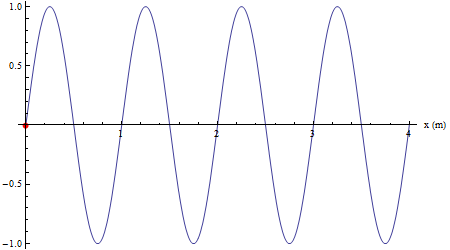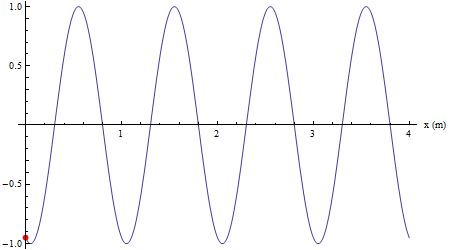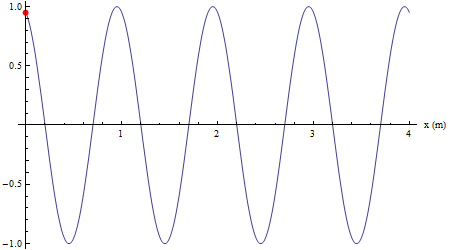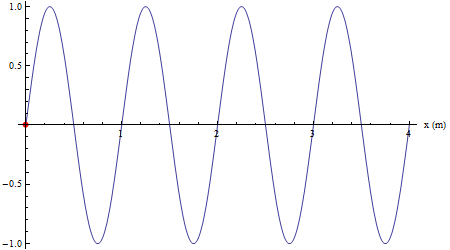
Infine si mostra come un qualsiasi altro punto investito dalla perturbazione riproduca il moto armonico della sorgente con un ritardo collegato alla velocità di propagazione (in color nero un punto in concordanza di fase con la sorgente, in verde un punto in opposizione di fase con la sorgente).

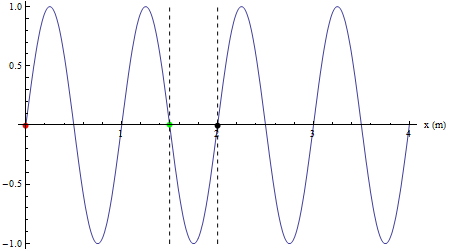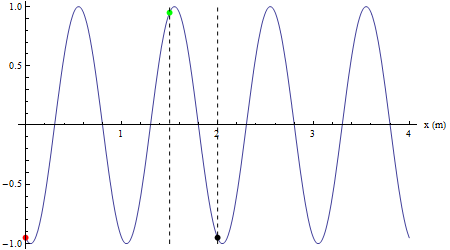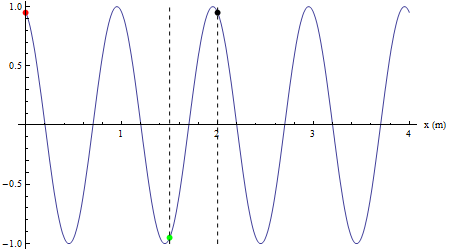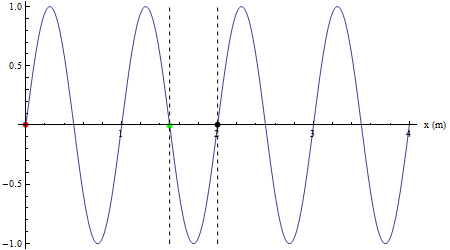
Verso della propagazione
L'animazione sottostante mostra come un cambio nel segno del coefficiente della variabile t implichi una propagazione nel verso delle ascisse negative dell'asse spaziale ossia l'onda possiede velocità opposta alle onde precedenti. Nel caso di componente negativa della velocità l'onda si dice regressiva (se positiva invece, si dice progressiva).
Velocità di propagazione
La successiva animazione mostra un singolo impulso sinusoidale generato da un'unica oscillazione armonica completa della sorgente. La durata di questa oscillazione è di un periodo T e nel frattempo l'onda si propaga ad una distanza pari alla sua lunghezza d' onda λ.
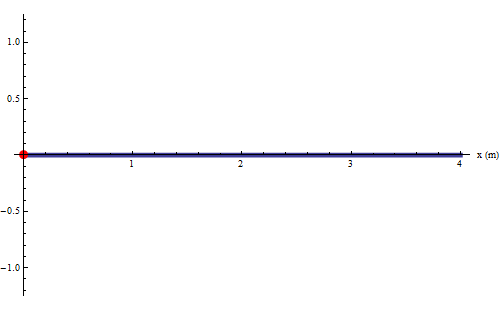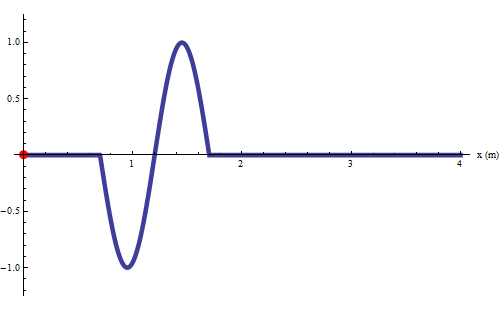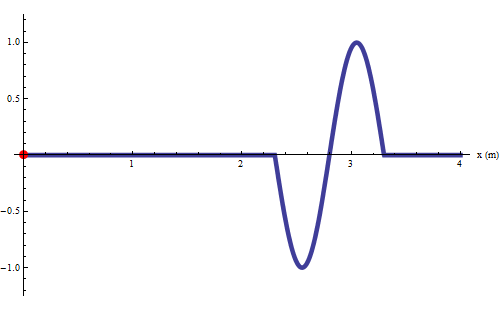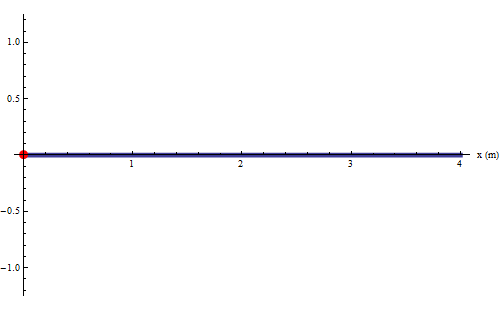
La velocità di propagazione è pertanto
![]()
essendo f=1/T la frequenza.
Battimenti e principio si sovrapposizione
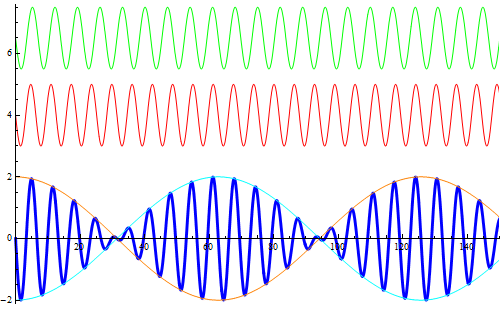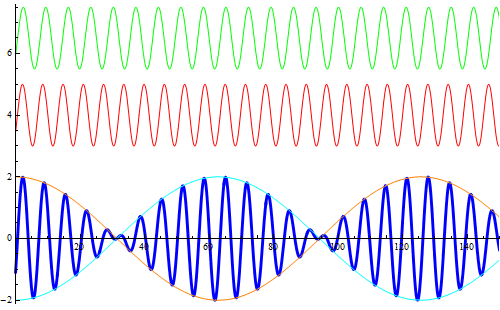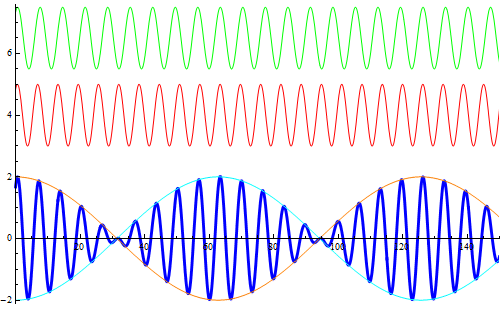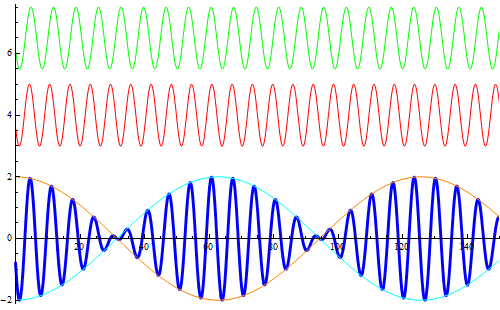
Si rappresentano due onde armoniche (l'asse orizzontale è un asse temporale) con frequenze leggermente diverse (la prima di ![]() , la seconda di
, la seconda di ![]() ) e, in blu, la loro sovrapposizione al variare della fase. La simulazione descrive ottimamente il fenomeno dei battimenti sonori la cui registrazione appare in un editor sonoro come nella figura successiva.
) e, in blu, la loro sovrapposizione al variare della fase. La simulazione descrive ottimamente il fenomeno dei battimenti sonori la cui registrazione appare in un editor sonoro come nella figura successiva.

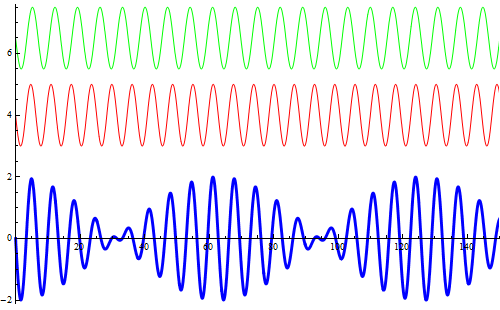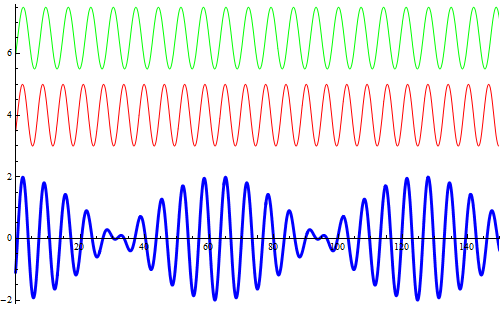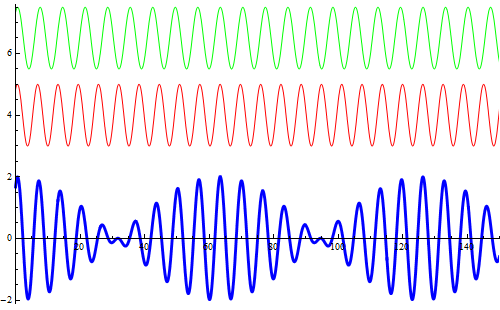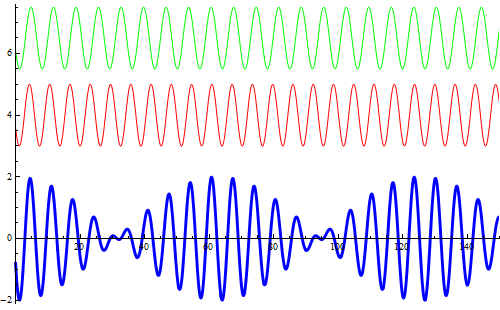
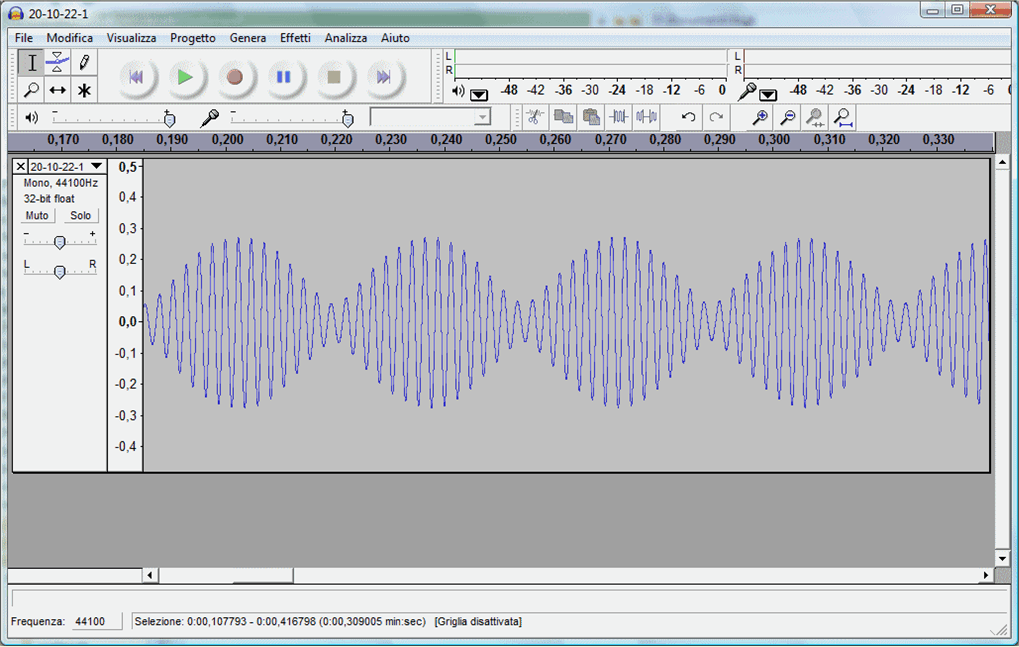
Registrazione sonora di un battimento tra due diapason.
Nella figura successiva viene visualizzata la curva responsabile della modulazione dell'ampiezza.
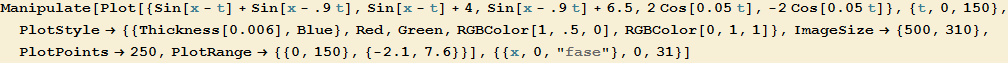
Onde stazionarie e principio di sovrapposizione
Onde che si propagano in versi opposti ma caratterizzate dalla medesima frequenza e lunghezza d'onda danno luogo, sovrapponendosi, ad onde stazionarie che non mostrano alcuna propagazione ma solo una oscillazione armonica di ciascun punto. Le posizioni dei ventri e dei nodi sono ben definite così come la loro distanza dalla sorgente (origine).


Impulsi e principio di sovrapposizione
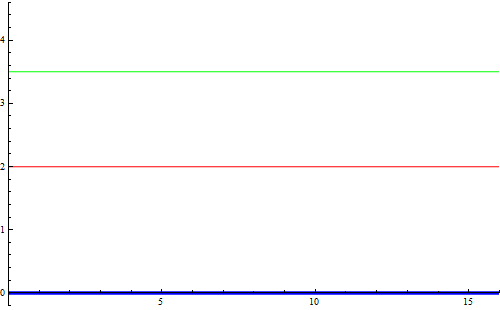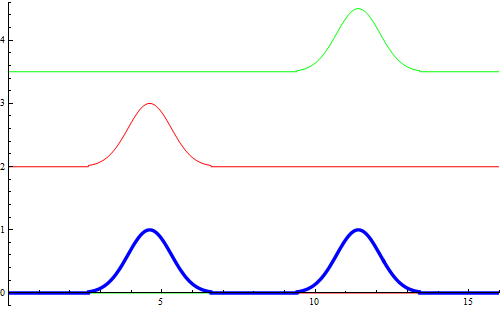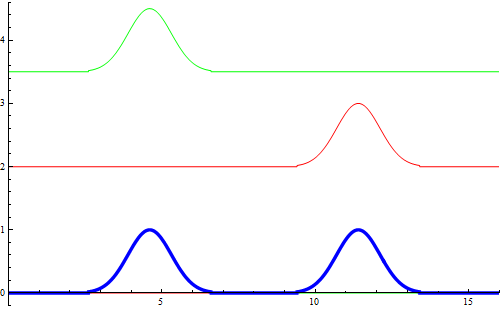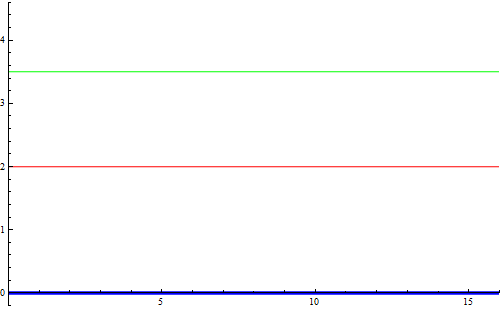
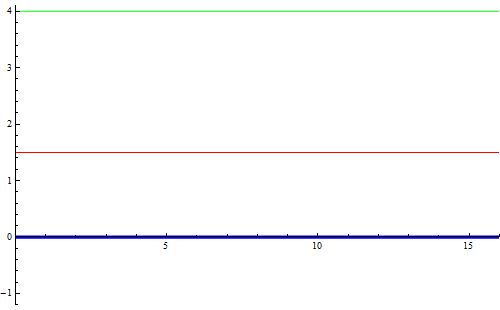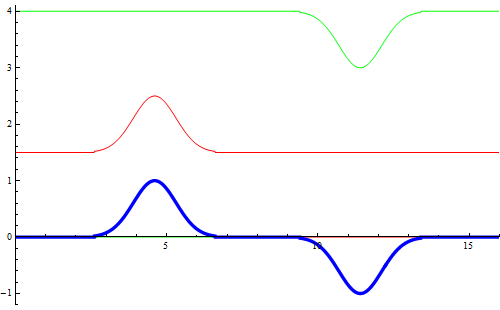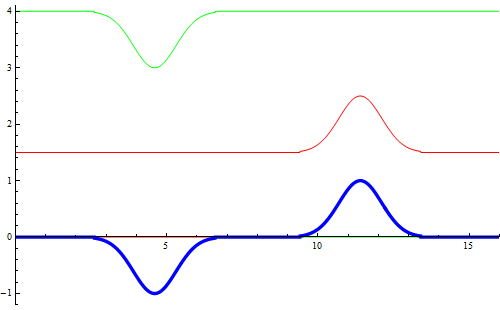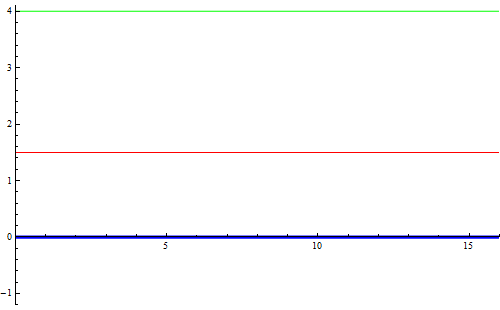
La figura mostra l'interferenza di due impulsi che si propagano in verso opposto ed interferiscono. Ciascuno si propaga indipendentemente dall'altro e l'impulso risultante (in blu) è semplicemenente la somma di ciascuno.
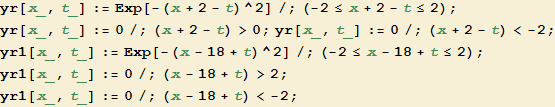
Due impulsi simili che si propagano in verso opposto ed interferiscono

Interferenza di due impulsi di valore opposto e che si propagano in verso opposto.

Ritorna alla pagina di presentazione