Lorenzo Roi (novembre 2009)
Generalizzazione
In quest'ultima parte cercheremo di generalizzare il concetto di curvatura esplicitando la dipendenza della derivata presente a primo membro della relazione dimostrata per la circonferenza
![]()
in termini delle funzioni rappresentative che descrivono la curva. A tale scopo daremo delle espressioni per i due differenziali che la costituiscono.
Sia quindi γ : {x(t),y(t)} una curva regolare descritta parametricamente. Se dt è il differenziale del parametro t, in corrispondenza di tale variazione sappiamo che i differenziali di ciascuna coordinata del punto generico P sono
| | (7) |
Questi descrivono la variazione delle coordinate del punto P per cui il vettore ds parallelo e concorde al versore tangente e il cui modulo esprime la lunghezza dell'arco ds, si ottiene facilmente con il teorema di Pitagora (figura 22) ed è dato da
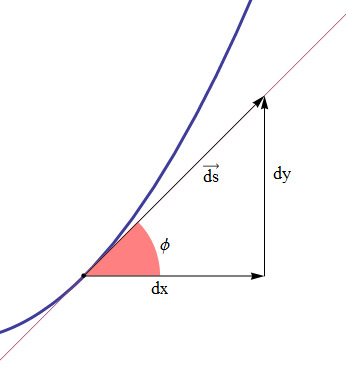
figura 22
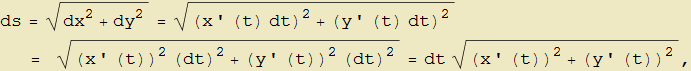
e se omettiamo la derivazione rispetto al parametro t si riscrive come
| | (8) |
Determiniamo ora l'espressione del differenziale dell'angolo che il versore tangente fa con una direzione qualsiasi per esempio quella dell'asse x di un sistema cartesiano. Questo differenziale coincide con il differenziale dell'angolo al centro della circonferenza osculatrice che, come visto, descrive pure la rotazione di tale versore. Riferendoci sempre alla figura 22 risulta che la tangente goniometrica dell'angolo φ è data da
![]()
che per le espressioni (7) diviene
![]()
Supposto che sia x'(t) ≠ 0 deduciamo pure
![]()
per cui non ci resta che eseguire la differenziazione
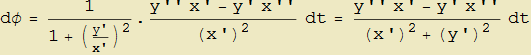
relazione che rimane valida anche indipendentemente dalla condizione x'(t) ≠ 0. Mettendo assieme quest'ultima con la (8) possiamo infine ottenere il rapporto dφ/ds come
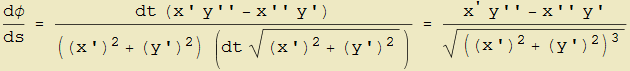
e quindi, dato che tale grandezza può essere negativa, definire la curvatura orientata di una curva γ : {x(t), y(t)} come
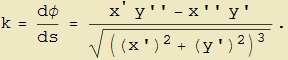 | (9) |
Questa espressione ci permette finalmente di determinare la seconda caratteristica intrinseca di una curva piana e, cosa particolarmente importante, indipendentemente dal calcolo esplicito, spesso arduo, della derivata dell'angolo rispetto alla lunghezza d'arco.
Volendo infine salvaguardare il collegamento tra curvatura e raggio di curvatura, grandezza quest'ultima positiva, si dovrà invece considerare il valore assoluto della curvatura orientata per cui
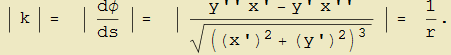 | (10) |
Applichiamo l'importante risultato (9), inizialmente per confermare quanto ottenuto con approccio geometrico in precedenza per la parabola e l'ellisse. In seguito determineremo l'andamento della curvatura di alcune curve chiarendo il significato del suo segno.
La curvatura dell'ellisse ε : {a cos t, b sen t} di semiassi a e b che si deduce dalla (9) è
![]()
che, nel caso di a = 2 e b = 1 coincide, a meno di trasformazioni goniometriche con il risultato già trovato.
Per la parabola ![]() si ha
si ha
![]()
che pure coincide con il risultato già dedotto se si pone a = 1.
Funzione seno
Se parametrizziamo la funzione seno come {t, sin t} la sua curvatura assume la forma

il cui grafico è riportato nella figura 23 assieme alla funzione stessa dato che l'ascissa coincide con il parametro.
![Graphics:FormBox[StyleBox[RowBox[{Funzione sin(x) e sua curvatura orientata, Cell[]}], RGBColor[0, 0, 1], FontFamily -> Helvetica, StripOnInput -> False], TraditionalForm]](HTMLFiles/index_187.gif)
figura 23
Funzione cubica
Data la funzione cubica dispari di equazione ![]() parametrizzata in
parametrizzata in ![]() la sua curvatura è
la sua curvatura è
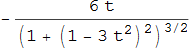
che, rappresentata assieme alla stessa cubica, mostra l'andamento di figura 24
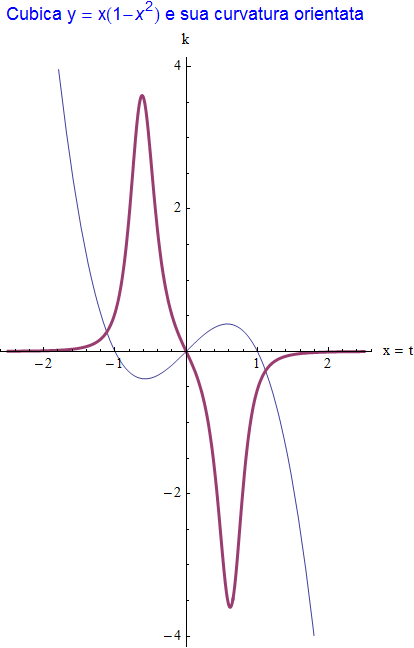
figura 24
Funzione di Lissajous
Definita la funzione di Lissajous lj : {2 cos t, sin (2t)}, della quale abbiamo già fornito il grafico nella prima parte, la sua curvatura risulta
mentre il grafico (fig. 25) è
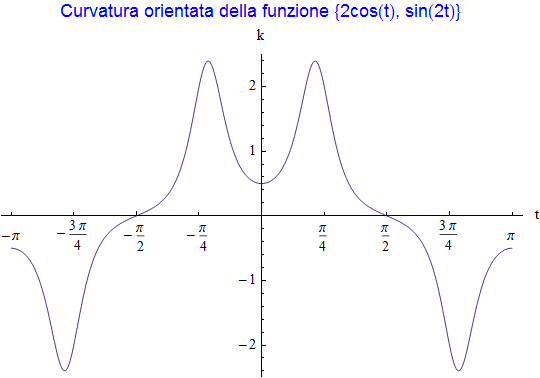
figura 25
Circonferenza
Riprendiamo infine il semplice esempio della circonferenza di raggio unitario per fornire la chiave interpretativa del segno della curvatura. Nella prima rappresentazione grafica (fig. 26a) la curva, parametrizzata come {cos t, sin t}, viene percorsa in verso antiorario e la curva piega verso sinistra rispetto alla direzione del versore tangente: nella seconda (fig. 26b) la medesima curva parametrizzata come γ : {cos(-t), sin(-t)} è percorsa in verso orario e quindi la circonferenza piega verso destra. In corrispondenza il versore tangente ruota in verso antiorario nel primo caso (e quindi la variazione dell'angolo è positiva), ruota in verso orario nel secondo. Tutto ciò si riflette sul segno della curvatura, positiva e unitaria nel primo, pari a -1 nel secondo.
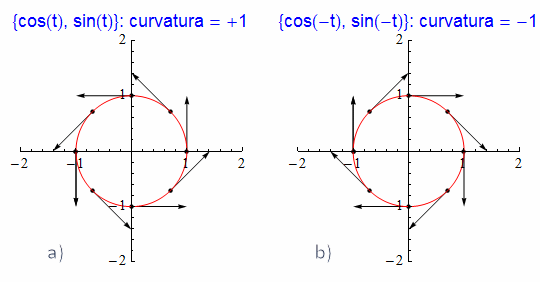
figura 26 a, b
Alla stessa conclusione si perviene osservando gli esempi precedenti del seno, della cubica o della funzione di Lissajous. Difatti, individuata la direzione del versore tangente, là dove la curva piega rispetto a questa direzione verso sinistra ossia il versore tangente tende a ruotare in verso antiorario la curvatura orientata appare di segno positivo mentre al contrario, la curvatura è negativa se la curva piega verso destra e il versore tangente ruota in verso orario.
Osservazione
La rappresentazione finora utilizzata della circonferenza con centro nell'origine è stata la seguente: γ : {r cos t, r sin t} con r misura del raggio e 0 ≤ t < 2π. Una rappresentazione parametrica alternativa meno nota è invece
![]()
che, comunque, non comprende il punto (-r, 0). A conferma dell'indipendenza della curvatura dalla particolare parametrizzazione entrambe forniscono come curvatura il valore 1/r.
Centro di curvatura ed evoluta
Per completare il percorso seguito intendiamo qui dedurre le coordinate del centro di curvatura per poi rappresentarne l'andamento in corrispondenza di alcune curve. A tal fine vanno riprese due osservazioni già esposte:
Queste due osservazioni ci permettono di risolvere con relativa facilità il problema. Difatti data la curva γ : {x(t),y(t)},
la retta normale nel punto ![]() corrispondente al valore
corrispondente al valore ![]() del parametro è individuata non appena si abbia il versore normale. Per quanto visto tale versore è
del parametro è individuata non appena si abbia il versore normale. Per quanto visto tale versore è
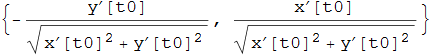
e si ottiene da quello tangente con una rotazione antioraria di 90°. La retta normale è quindi in forma parametrica
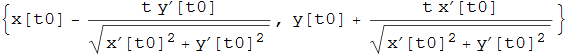
dove il parametro t esprime sostanzialmente la coordinata di un punto sulla normale a partire da ![]() considerato come origine. Pertanto se sostituiamo a t il valore con segno del raggio di curvatura
considerato come origine. Pertanto se sostituiamo a t il valore con segno del raggio di curvatura ![]() potremo correttamente individuare il centro C: difatti se
potremo correttamente individuare il centro C: difatti se ![]() il centro sarà disposto ad una distanza
il centro sarà disposto ad una distanza ![]() da
da ![]() concordemente al versore normale (animazione di fig. 27 con t < 0) mentre se
concordemente al versore normale (animazione di fig. 27 con t < 0) mentre se ![]() apparterrà alla semiretta normale che non contiene il versore normale (fig. 27 e t > 0).
apparterrà alla semiretta normale che non contiene il versore normale (fig. 27 e t > 0).
figura 27
Non ci resta che sostituire al parametro t nella retta normale il valore del raggio di curvatura nel punto ![]() ottenendo
ottenendo
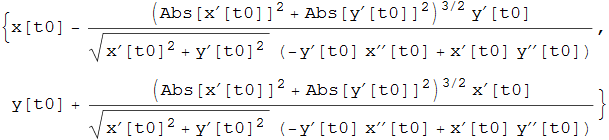
Riportando il tutto in funzione di t, otteniamo infine il luogo dei centri di curvatura
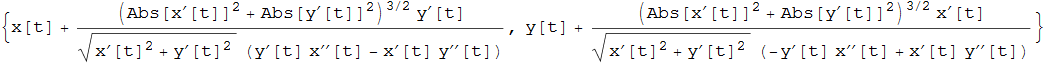
Tale luogo viene detto evoluta della curva. Siamo quindi in grado di associare ad ogni curva regolare una seconda curva, la sua evoluta. Di seguito riportiamo alcuni esempi di curve e rispettive evolute evidenziando in colore i raggi di curvatura di un opportuno numero di punti della curva.
Di seguito e in conclusione, presentiamo un piccolo catalogo prevalentemente visuale di curve e relative evolute tracciando in colore pure un certo numero di raggi di curvatura.
Astroide
La curva dell'astroide (detta anche asteroide) si rappresenta parametricamente tramite la coppia di funzioni ![]() . Il centro di curvatura è descritto dalla coppia di funzioni seguente e la fig. 28 ne riporta il grafico assieme a quello della curva originaria.
. Il centro di curvatura è descritto dalla coppia di funzioni seguente e la fig. 28 ne riporta il grafico assieme a quello della curva originaria.
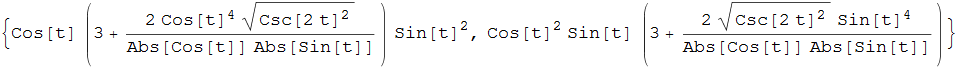
figura 28
Se in aggiunta, tracciamo anche un certo numero di rette normali la figura che emerge (fig. 29) suggerisce come l'evoluta si possa considerare anche come quella curva tangente a ciascuna retta normale ossia costituisca l'inviluppo delle rette normali.
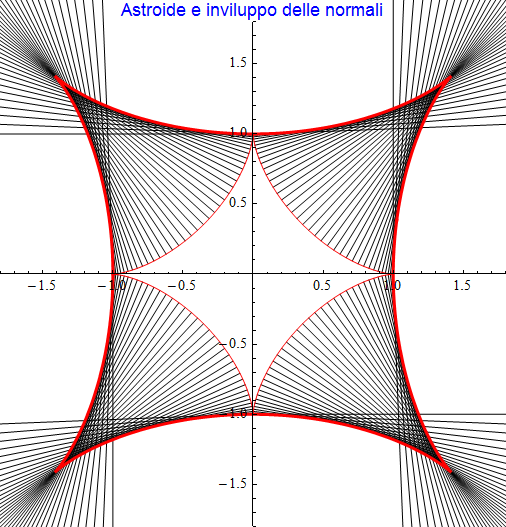
figura 29
Tracciando solo i raggi dei cerchi osculatori si ottiene una conferma grafica di ciò (fig. 30).
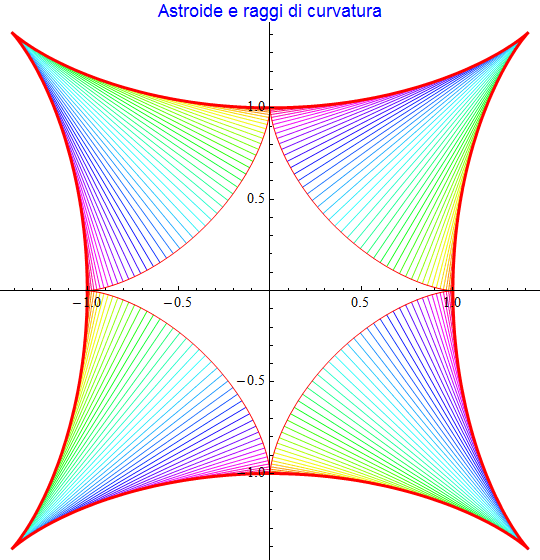
figura 30
Cardioide
L'evoluta di una cardioide {2 cos(t) - cos(2t), 2 sin(t) - sin(2t)} è un'altra cardioide in quanto il luogo dei centri di curvatura è dato da
figura 31
Nella figura 32 e nella analoghe che seguono, forniamo entrambe le curve con evidenziati in colore un certo numero di raggi di curvatura.
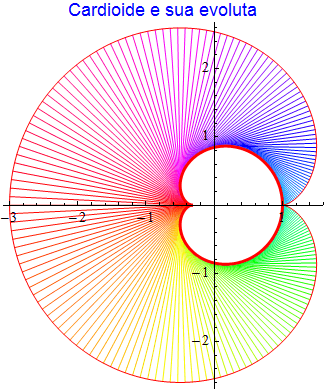
figura 32
Cissoide di Diocle
Le funzioni che descrivono la cissoide di Diocle sono {t2/(1 + t2), t3/(1 + t2)} e, in corrispondenza, l'evoluta risulta
figura 33
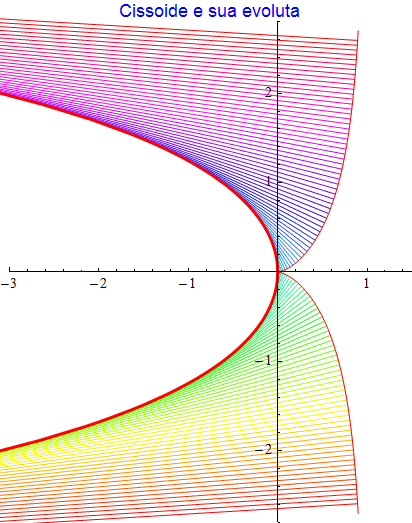
figura 34
Strofoide
La strofoide è data dalla coppia {(t2 - 1)/(1 + t2), t(t2 - 1)/(1 + t2)} e in corrispondenza il luogo dei centri di curvatura risulta
figura 35
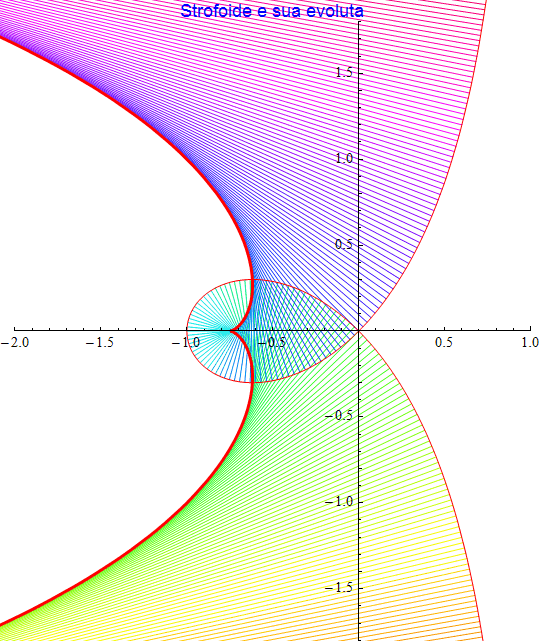
figura 36
Lemniscata di Bernoulli
La lemniscata di Bernoulli è rappresentata come {sin(t)/(1 + cos2(t)), (sin(t)cos(t))/(1 + cos2(t))} mentre la sua evoluta risulta
figura 37
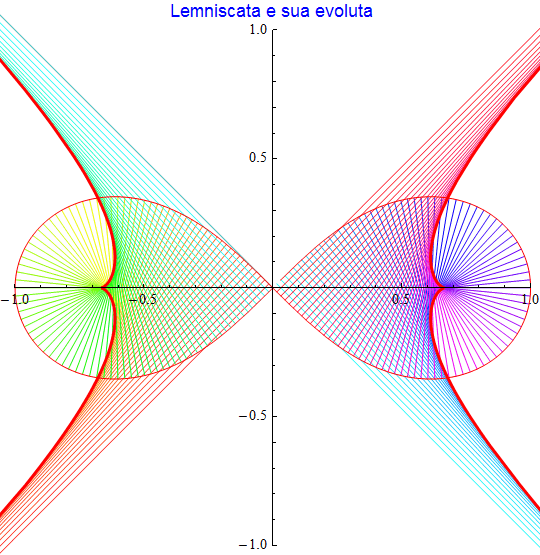
figura 38
Versiera della Agnesi
La rappresentazione della curva versiera è {2 t, 2/(1 + t2)} e possiede l'evoluta
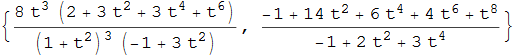
figura 39
La curvatura di tale curva mostra l'andamento di fig. 40
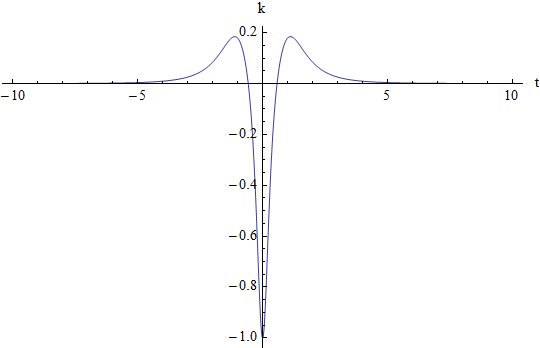
figura 40
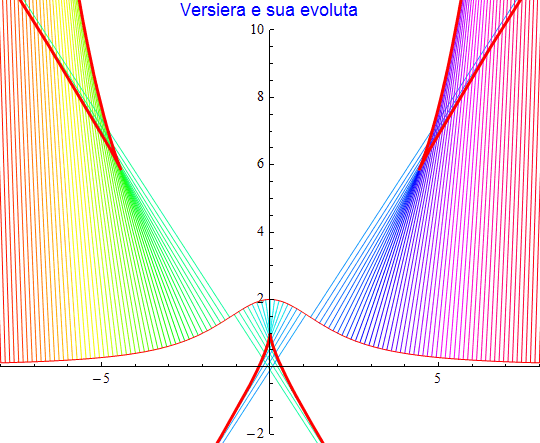
figura 41
Cicloide
Come la curva cardioide anche l'evoluta di una cicloide {t - sin(t), 1 - cos(t)} è ancora una cicloide come appare dalla rappresentazione seguente.
figura 42
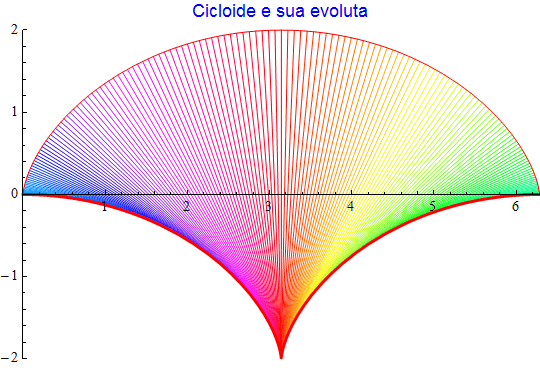
figura 43
Spirale logaritmica
Anche la spirale logaritmica descritta dalle {exp(t/7) cos(t), exp(t/7) sin(t)} possiede una evoluta dello stesso tipo
mentre la sua curvatura è sostanzialmente la funzione esponenziale
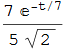
figura 44
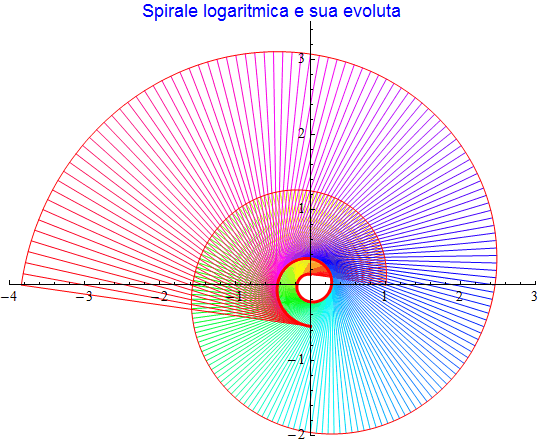
figura 45
Nella successiva immagine sono invece tracciate le circonferenze osculatrici con in evidenza nella parte centrale l'evoluta.
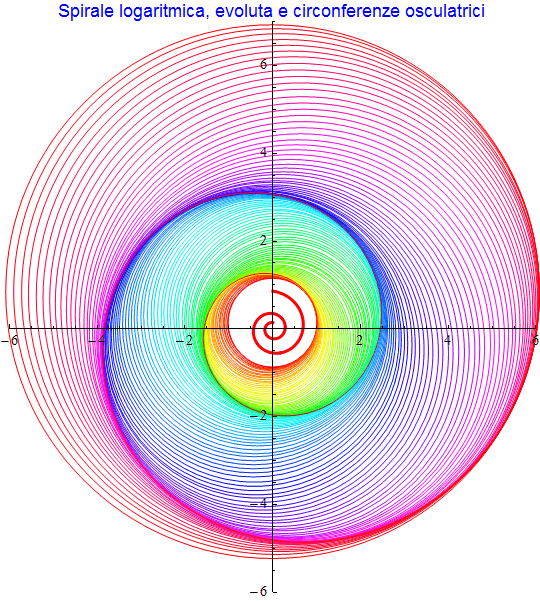
figura 46
Cubica
La funzione cubica parametrizzata come {t, t2(1 - t)} possiede evoluta descritta dalla coppia di funzioni
figura 47
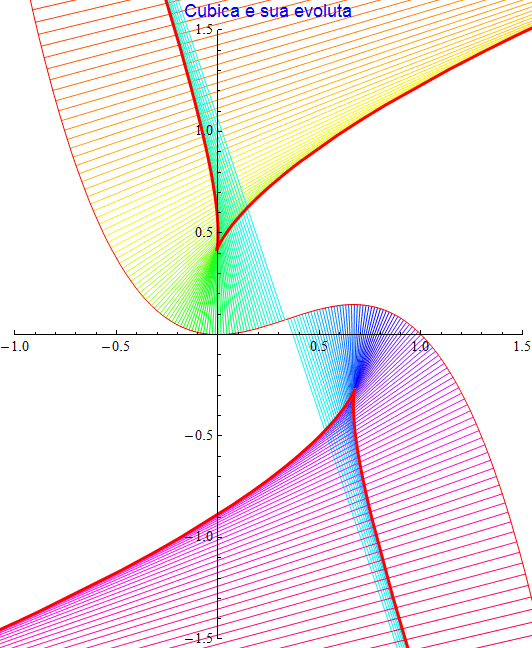
figura 48
Bibliografia
Ritorna all'inizio.