Lorenzo Roi (novembre 2009)
Parte seconda: sulla curvatura di una circonferenza
Nella prima parte di questo lavoro abbiamo visto che il versore tangente a una curva in un suo punto dipende solo dall'orientazione ma non dalla particolare rappresentazione della curva. Come detto quindi, tale versore descrive una proprietà locale della curva stessa indipendente dal parametro scelto ma dipendente solo dal punto della curva. In questa parte approfondiamo una seconda importante proprietà delle curve regolari ossia la loro curvatura: per far ciò dovremo chiarire come varia il versore tangente.
È evidente che se si considera la rappresentazione discussa nella prima parte di una retta la cui direzione sia individuata dal vettore u
![]()
il versore tangente t si ottiene dividendo u per il suo modulo ![]() e questo, al variare del punto P sulla retta, non modifica la sua direzione ossia, detto in altro modo, non subisce alcuna rotazione o ancora in modo equivalente, il suo angolo di rotazione è nullo. È per questo che, a livello intuitivo, associamo ad una retta una curvatura nulla. In un qualsiasi altro caso il versore t potrà invece variare la sua direzione ossia subirà una rotazione di qualche angolo. Vediamo come possiamo tener conto di ciò nel caso particolare della circonferenza.
e questo, al variare del punto P sulla retta, non modifica la sua direzione ossia, detto in altro modo, non subisce alcuna rotazione o ancora in modo equivalente, il suo angolo di rotazione è nullo. È per questo che, a livello intuitivo, associamo ad una retta una curvatura nulla. In un qualsiasi altro caso il versore t potrà invece variare la sua direzione ossia subirà una rotazione di qualche angolo. Vediamo come possiamo tener conto di ciò nel caso particolare della circonferenza.
Se ![]() è il versore associato ad un punto A della circonferenza γ : {r cos t, r sin t} con centro nell'origine del sistema cartesiano e raggio r mentre
è il versore associato ad un punto A della circonferenza γ : {r cos t, r sin t} con centro nell'origine del sistema cartesiano e raggio r mentre ![]() corrisponde al punto B molto prossimo ad A e ottenuto sommando al parametro t l'incremento h, la rotazione subita da t nel passaggio tra A e B è rappresentata dall'angolo h = dφ di figura 13 e definito dall'intersezione delle rette tangenti in A e B.
corrisponde al punto B molto prossimo ad A e ottenuto sommando al parametro t l'incremento h, la rotazione subita da t nel passaggio tra A e B è rappresentata dall'angolo h = dφ di figura 13 e definito dall'intersezione delle rette tangenti in A e B.
figura 13
Se C è il punto d'intersezione di queste rette tangenti, collegando A e B con il centro O della circonferenza, si viene a formare un quadrilatero OACB con gli angoli ∠AOB e ∠ACB supplementari. Ne segue che l'angolo dφ di cui è ruotato t è anche uguale all'angolo al centro ∠AOB = dφ essendo supplementari allo stesso angolo ∠ACB. Poiché in corrispondenza di questa variazione angolare il tratto di circonferenza che collega A con B ossia la lunghezza dell'arco sotteso dall'angolo al centro dφ risulta pari a ds = r dφ, ne discende che il rapporto tra queste due variazioni (differenziali) è
![]()
Pensando il punto B variabile sulla circonferenza, il rapporto a primo membro in sostanza collega la rotazione subita dal versore tangente con la corrispondente lunghezza del tratto di curva percorso dallo stesso punto. Siccome tali osservazioni si possono estendere immutate a qualsiasi altro punto della circonferenza, possiamo affermare che in una circonferenza il rapporto dei differenziali dφ/ds ossia la derivata dell'angolo di rotazione del versore tangente eseguita rispetto alla lunghezza dell'arco corrispondente, è una costante pari a 1/r. Una seconda esemplificazione ci permetterà di perfezionare ulteriormente il concetto intuitivo di curvatura.
Consideriamo pertanto due circonferenze ![]() e
e ![]() , con raggi rispettivamente
, con raggi rispettivamente ![]() ,
, ![]() e tali che
e tali che ![]() . Da un punto di vista formale, per quanto precede, la derivata dφ/ds assume in ciascun punto delle due circonferenze, rispettivamente i valori
. Da un punto di vista formale, per quanto precede, la derivata dφ/ds assume in ciascun punto delle due circonferenze, rispettivamente i valori
![]()
e dove per le condizioni poste, la prima è maggiore della seconda
![]()
Ne segue che a parità di arco percorso da un punto generico sulle due circonferenze, l'angolo di rotazione del versore tangente è maggiore nella prima circonferenza rispetto a quello nella seconda. Questo fatto si può cogliere anche visivamente se rappresentiamo l'angolo di rotazione di t (figura 14):
figura 14
in ciascuna circonferenza la lunghezza dell'arco che collega il punto iniziale A con quello finale B è la medesima ma evidentemente l'angolo di rotazione appare maggiore nel caso della circonferenza di raggio minore. In particolare, essendo nella figura ![]() l'angolo di cui ruota il versore nella prima è sempre il doppio della seconda. Tutto ciò giustifica come si possa intuitivamente associare alla prima circonferenza una curvatura maggiore della seconda e pertanto definire provvisoriamente il concetto di curvatura k tramite la derivata k = dφ/ds.
l'angolo di cui ruota il versore nella prima è sempre il doppio della seconda. Tutto ciò giustifica come si possa intuitivamente associare alla prima circonferenza una curvatura maggiore della seconda e pertanto definire provvisoriamente il concetto di curvatura k tramite la derivata k = dφ/ds.
In ultima analisi, per una circonferenza la curvatura è costante in tutti i suoi punti e si ottiene con il rapporto tra la variazione di angolo al centro qualsiasi (anche infinitesimo) e l'arco che lo sottende. Sempre per la circonferenza abbiamo pure una relazione che lega la curvatura con il raggio: le due grandezze sono inversamente proporzionali. In particolare, se r → ∞ la curvatura k → 0 per cui tende ad annullarsi. Quest'ultima osservazione è, ancora una volta, coerente con la nozione intuitiva di curvatura giacché una circonferenza con raggio via via più grande tende ad assomigliare ad una retta e quindi ad assumere una curvatura nulla.
Esempi di curvatura
Così come si è costruito il versore tangente in un punto di una curva regolare vediamo se
Consideriamo la semplice parabola di equazione esplicita ![]() e che nella sua parametrizzazione più immediata e già utilizzata diviene
e che nella sua parametrizzazione più immediata e già utilizzata diviene ![]() . Se
. Se ![]() è un suo punto, detto h un incremento positivo, siano
è un suo punto, detto h un incremento positivo, siano
![]()
due altri suoi punti. Nel caso non siano allineati si potrà certamente associare a questi tre punti una circonferenza e quindi il relativo centro C(α, β) e raggio r.
Con il supporto simbolico di Mathematica (si veda la funzione cfr3Punti e relativi commenti nel notebook associato), le coordinate del centro e del raggio sono le soluzioni del sistema,
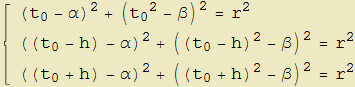
e risultano, per il centro C
mentre il raggio è
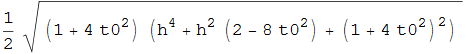
Evidentemente queste grandezze dipendono dal punto ![]() e quindi dal parametro
e quindi dal parametro ![]() e dall'incremento h: se fissiamo
e dall'incremento h: se fissiamo ![]() e h=0.8 otteniamo la figura 15 che rappresenta sia la parabola e sia la circonferenza con relativo centro C.
e h=0.8 otteniamo la figura 15 che rappresenta sia la parabola e sia la circonferenza con relativo centro C.
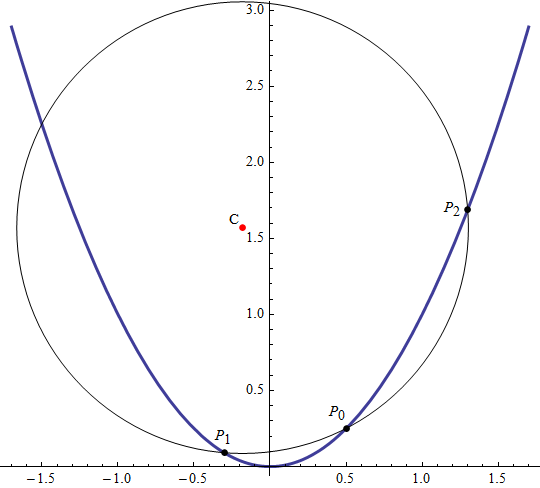
figura 15
Nello stesso modo seguito per la costruzione del vettore tangente potremo associare al punto ![]() una circonferenza univocamente determinata se esistono finiti al tendere allo zero dell'incremento h, il limite del raggio
una circonferenza univocamente determinata se esistono finiti al tendere allo zero dell'incremento h, il limite del raggio
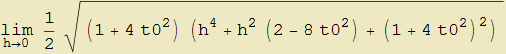
e ciascuno dei due limiti riguardanti le coordinate del centro
![]()
Nell'esempio questi limiti non presentano particolari difficoltà (conducono dopo opportune semplificazioni a funzioni continue di h) e forniscono rispettivamente il raggio (che chiameremo raggio di curvatura locale)
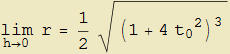
mentre i rimanenti danno le coordinate del centro (detto centro di curvatura locale)
![]()
ossia
![]()
La supposizione iniziale appare quindi percorribile: siamo in grado di associare ad ogni punto ![]() della parabola una circonferenza (detta osculatrice) di opportuni centro e raggio. Utilizzando la proporzionalità inversa tra curvatura k e raggio r rilevata per la circonferenza, potremo ottenere la curvatura della parabola nel punto
della parabola una circonferenza (detta osculatrice) di opportuni centro e raggio. Utilizzando la proporzionalità inversa tra curvatura k e raggio r rilevata per la circonferenza, potremo ottenere la curvatura della parabola nel punto ![]() come
come
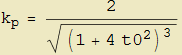
Un'altra conseguenza geometrica di tale approccio si deduce osservando che le rette secanti la curva e passanti rispettivamente per le coppie di punti ![]() ,
, ![]() e per
e per ![]() ,
, ![]() convergono entrambe alla retta tangente in
convergono entrambe alla retta tangente in ![]() in quanto
in quanto ![]() e
e ![]() nello stesso modo con cui abbiamo ottenuto il vettore tangente. Ne segue che tale circonferenza avrà in
nello stesso modo con cui abbiamo ottenuto il vettore tangente. Ne segue che tale circonferenza avrà in ![]() la medesima tangente della curva γ e le due curve sono quindi mutuamente tangenti. Si dice, in tale contesto, che esse hanno un contatto in
la medesima tangente della curva γ e le due curve sono quindi mutuamente tangenti. Si dice, in tale contesto, che esse hanno un contatto in ![]() almeno di ordine tre. L'avere la medesima tangente comporta la coincidenza anche della retta normale per
almeno di ordine tre. L'avere la medesima tangente comporta la coincidenza anche della retta normale per ![]() per questo nel seguito potremo individuare il centro istantaneo di curvatura come quel punto della normale avente distanza dal punto
per questo nel seguito potremo individuare il centro istantaneo di curvatura come quel punto della normale avente distanza dal punto ![]() pari al raggio di curvatura.
pari al raggio di curvatura.
Nella simulazione di fig. 16 è possibile variare il punto ![]() sulla parabola così come l'incremento h: portandolo a valori prossimi allo zero ci si può rendere conto come le circonferenze convergano verso quella osculatrice. Se invece si pone il valore dell'incremento pari allo zero si può analizzare come variano le circonferenze osculatrici al variare di
sulla parabola così come l'incremento h: portandolo a valori prossimi allo zero ci si può rendere conto come le circonferenze convergano verso quella osculatrice. Se invece si pone il valore dell'incremento pari allo zero si può analizzare come variano le circonferenze osculatrici al variare di ![]() e, in particolare, seguire il luogo dei centri di curvatura.
e, in particolare, seguire il luogo dei centri di curvatura.
figura 16
L'immagine seguente (fig. 17) associa, codificati con il medesimo colore, ad alcuni punti della parabola le corrispondenti circonferenze osculatrici e relativi centri.
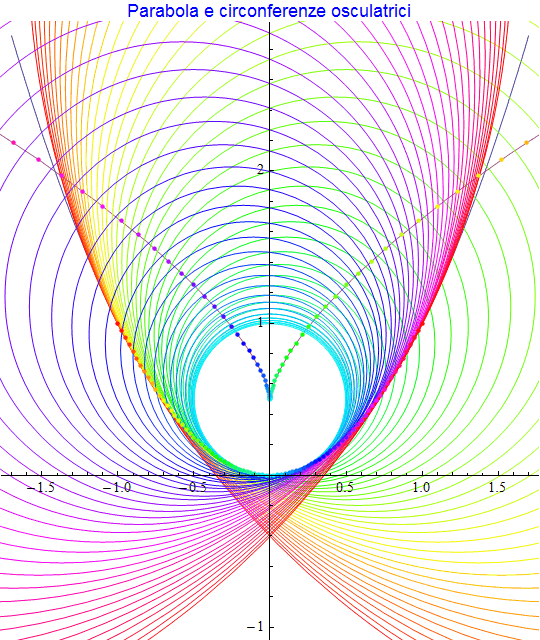
figura 17
Infine il grafico della curvatura ![]() della parabola (fig. 18) mostra come questa sia massima in corrispondenza del vertice
della parabola (fig. 18) mostra come questa sia massima in corrispondenza del vertice ![]() mentre tenda ad annullarsi per valori molto grandi del parametro.
mentre tenda ad annullarsi per valori molto grandi del parametro.
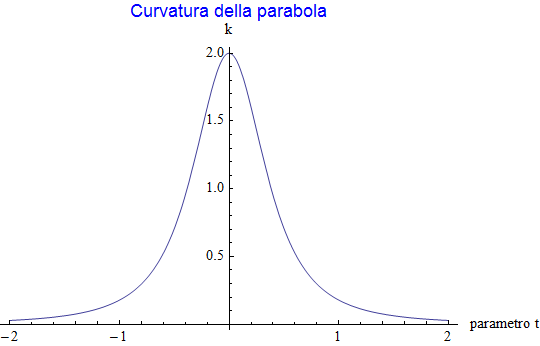
figura 18
Quale secondo esempio proponiamo lo studio della curvatura della ellisse con il semiasse orizzontale lungo 2 e quello verticale unitario: la sua rappresentazione è quindi ε : {2cos t, sin t}. Nello stesso modo seguito per la parabola, le coordinate del centro di una circonferenza passante per i suoi tre punti ![]() ,
, ![]() ,
, ![]() (definiti come nella parabola) risultano
(definiti come nella parabola) risultano
mentre il corrispondente raggio è
Passando al limite si ricavano le coordinate del centro di curvatura in funzione del parametro che individua il punto ![]()
e il raggio di curvatura
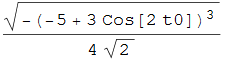
Nell'animazione seguente (fig. 19) variando il punto ![]() sull'ellisse in corrispondenza dell'incremento nullo si può seguire il luogo dei centri di curvatura mentre se h ≠ 0 viene visualizzata la circonferenza passante per i punti
sull'ellisse in corrispondenza dell'incremento nullo si può seguire il luogo dei centri di curvatura mentre se h ≠ 0 viene visualizzata la circonferenza passante per i punti ![]() ,
, ![]() ,
, ![]() .
.
figura 19
In alternativa si riporta un certo numero di circonferenze osculatrici (fig. 20) ciascuna avente un colore corrispondente al proprio centro e al punto di contatto con l'ellisse.
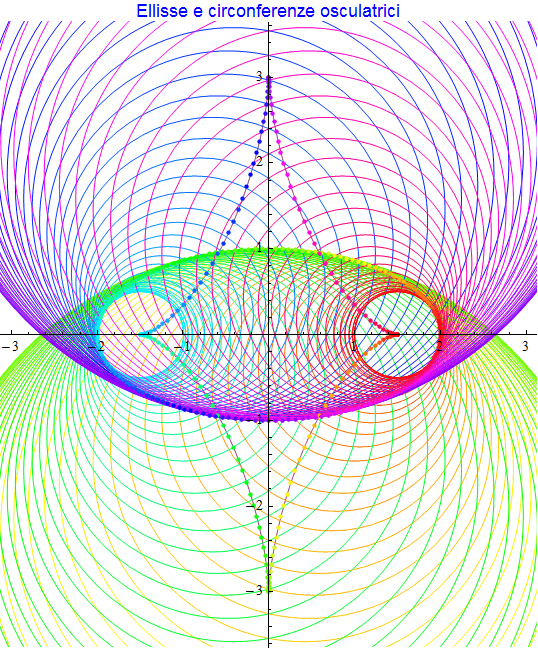
figura 20
Infine l'andamento della curvatura è dato dalla figura 21: appare manifestamente periodico (T = π) essendo l'ellisse una curva chiusa e simmetrica: la curvatura oscilla tra un valore massimo che viene raggiunto nei vertici di ascissa ±2 mentre nei rimanenti vertici assume la curvatura minima
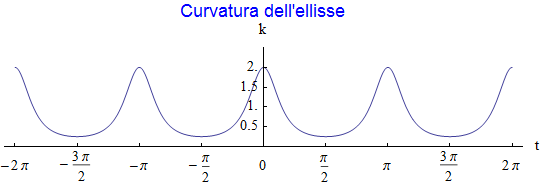
figura 21
Gli esempi sopra confermano la possibilità di associare ad ogni punto di una curva una circonferenza e quindi un raggio di curvatura r da cui derivare, per quanto detto nella sezione precedente, una curvatura k = 1/r. Siamo pure in grado di determinare il centro di curvatura identificandolo con il centro della circonferenza osculatrice.
Continua nella terza parte.