Ritorna alla pagina di presentazione
Sviluppi di Fourier di alcune forme d'onda
Lorenzo Roi (7 gennaio 2011)
Presentiamo in questa pagina gli sviluppi di Fourier delle principali forme d'onda (a dente di sega, triangolare, quadra) assieme alle rappresentazioni grafiche dell'ampiezza delle prime armoniche in relazione alla frequenza fondamentale e quindi come la loro sovrapposizione tenda ad approssimare la forma d'onda originaria.
(Le immagini che rappresentano la somma delle armoniche sono dei link a delle animazioni Flash)
Onda a dente di sega
La funzione d'onda a dente di sega è definita come
![]()
è periodica con periodo T e il suo sviluppo di Fourier è dato dalla serie
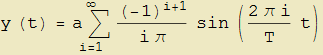
Il suo grafico (a = 1 e T = 1) risulta

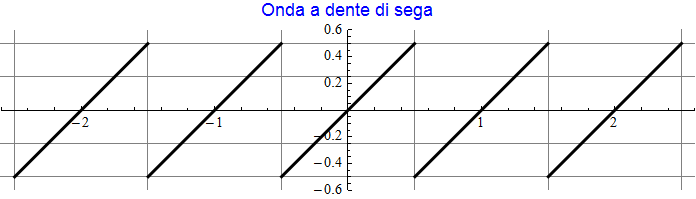
mentre le prime cinque armoniche sono
![]()

Supposta l'ampiezza dell'armonica fondamentale pari ad 1 così come la sua frequenza, l'ampiezza delle successive armoniche in funzione della frequenza è rappresentata dall’istogramma

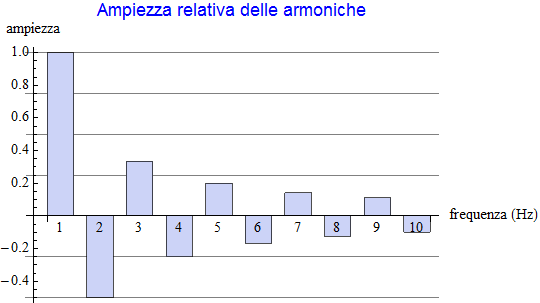
mentre la rappresentazione grafica che si ottiene al variare del numero di armoniche secondarie (per un massimo di 20) che la approssimano nella somma è data dal grafico seguente.

Onda triangolare
La funzione per un'onda triangolare è definita come
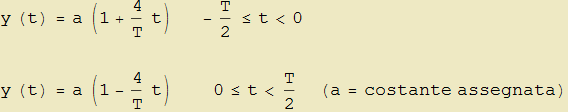
è periodica con periodo T e lo sviluppo di Fourier è
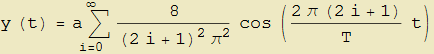
Il suo grafico (a = 1 e T = 1) è

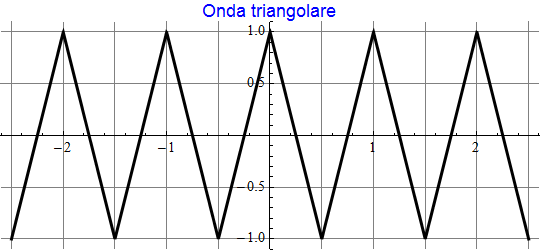
mentre le sue prime cinque armoniche sono le funzioni
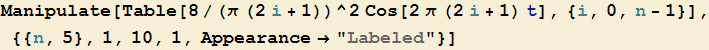

Supposta pari ad 1 l'ampiezza dell'armonica fondamentale così come la sua frequenza, l'ampiezza delle successive armoniche in funzione della frequenza è rappresentata dall'istogramma

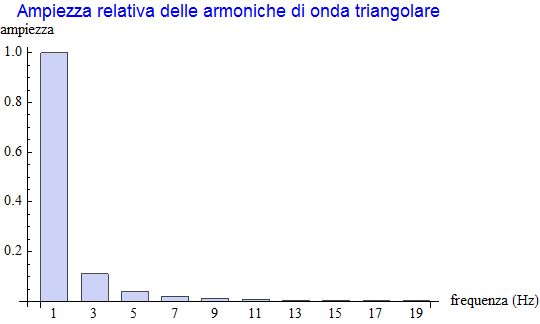
che mostra come l'ampiezza decresca rapidamente all'aumentare della frequenza. La rappresentazione grafica che si ottiene al variare del numero di armoniche secondarie (per un massimo di 10) è

Onda quadra
L'importante funzione onda quadra è definita come
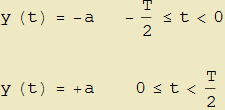
e possiede, come le precedenti, periodo T. Il suo sviluppo di Fourier è
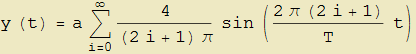
mentre il suo grafico risulta (a = 1 e T = 1)

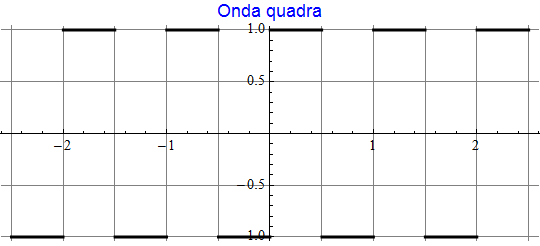
Le sue prime cinque armoniche sono le funzioni


e la loro ampiezza in rapporto all'armonica fondamentale decresce all'aumentare della frequenza come mostrato dall'istrogramma

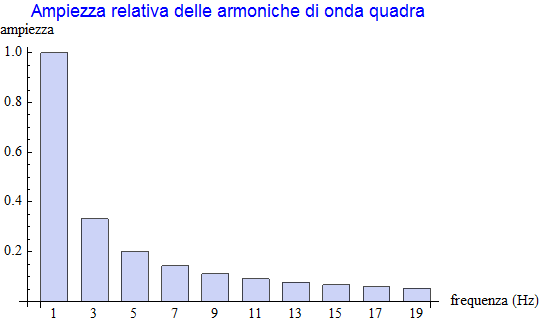
Infine, la somma delle armoniche fino ad un ordine massimo di 20 fornisce la rappresentazione grafica seguente

Ritorna alla pagina di presentazione