Parabola: costruzione n. 3

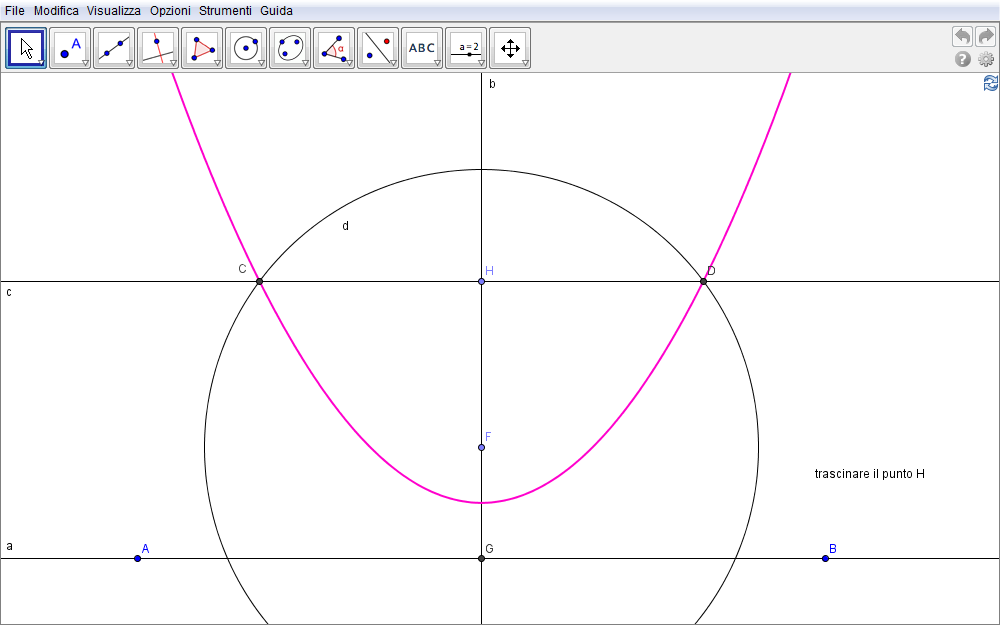
La costruzione si fonda sulla definizione di parabola e parte con l'assegnare

• la direttrice a
• e il punto F (il fuoco).
• Tracciato l'asse b perpendicolarmente alla direttrice per F, sia
• G la sua intersezione con a.
• Detta c una retta parallela alla direttrice passante per il generico punto H di b,
• si disegni quindi la circonferenza di centro F e raggio pari alla distanza HG di c da a. A tal fine si utilizzi lo strumento Compasso .
• I punti di intersezione P e Q di tale circonferenza con c sono equidistanti dal fuoco e dalla direttrice per cui, per definizione, appartengono alla parabola.

Figura 1.5. parabola05.ggb.

Trascinare il punto H per osservare l'appartenenza dei punti D e C alla parabola (tracciata come luogo).

Deduzione dell'equazione

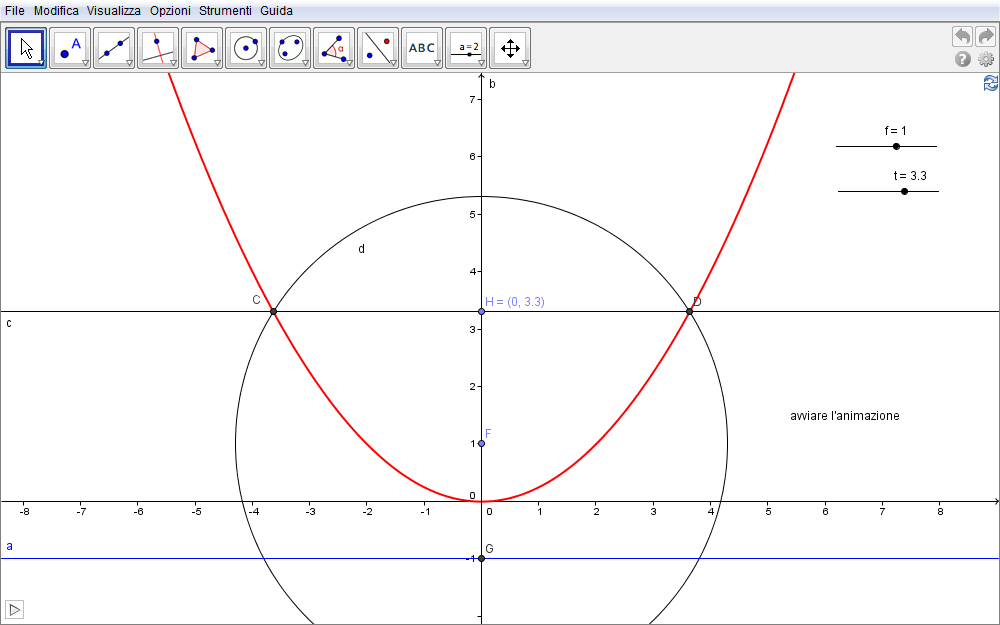
Per determinare l'equazione rappresentativa nella situazione descritta nella sezione precedente definiamo un sistema cartesiano con l'origine nel vertice V, punto medio del segmento GF (fig. 1.6).

Figura 1.6. parabola06.ggb.

Definiamo innanzitutto uno slider f cui faremo corrispondere l'ordinata del fuoco \(F(0,f)\) cosicché la direttrice avrà equazione \(y=-f\) e questa interseca in G l'asse delle ordinate. Un secondo slider t rappresentarà invece l'equazione del fascio di rette \(c:y=t\) per H e parallele alla direttrice. A parte gli slider, i punti F, G, la direttrice a, la retta c e la circonferenza d, sono introdotti nella fig. 1.6 tramite la barra di inserimento: per esempio, la retta c come y=t, la circonferenza come x^2 + (y - f)^2 = (t + f)^2 mentre C è individuato dal comando Intersezione[d, c].
Definito il punto \(H(0,t)\), il raggio della circonferenza di centro F risulta pari a \(GH=t-(-f)=t+f\) per cui i punti C e D di intersezione tra la retta c e questa circonferenza con coordinate \((x,y)\), sono le soluzioni del sistema \begin{equation}\cases{y=t\cr (x-0)^2+(y-f)^2=(t+f)^2.\cr}\end{equation} Volendo determinare il legame tra le coordinate x e y, è sufficiente inserire la prima nella seconda equazione ed eliminare la dipendenza da t, eseguire i quadrati e quindi ottenere \begin{equation}x^2+y^2-2fy+f^2=y^2+f^2+2fy\quad\Rightarrow\quad 4f y=x^2\quad\Rightarrow\quad y=\biggl(\!{1\over 4f}\!\biggr)x^2\end{equation} del tutto analoga all'equazione aspettata e già dedotta in altro modo.
Nella figura 1.6 avviare l'animazione dello slider t per osservare l'appartenenza dei punti C e D alla parabola definita, in questo caso, dall'equazione \(y=1/(4 f)\, x^2\) digitata direttamente dalla barra di inserimento.