Parabola: costruzione n. 1
La prima costruzione della parabola parte dalla sua definizione come luogo ossia
luogo geometrico dei punti P del piano tali da avere la distanza da un punto fisso F (il fuoco) uguale alla distanza da una retta data (la direttrice).
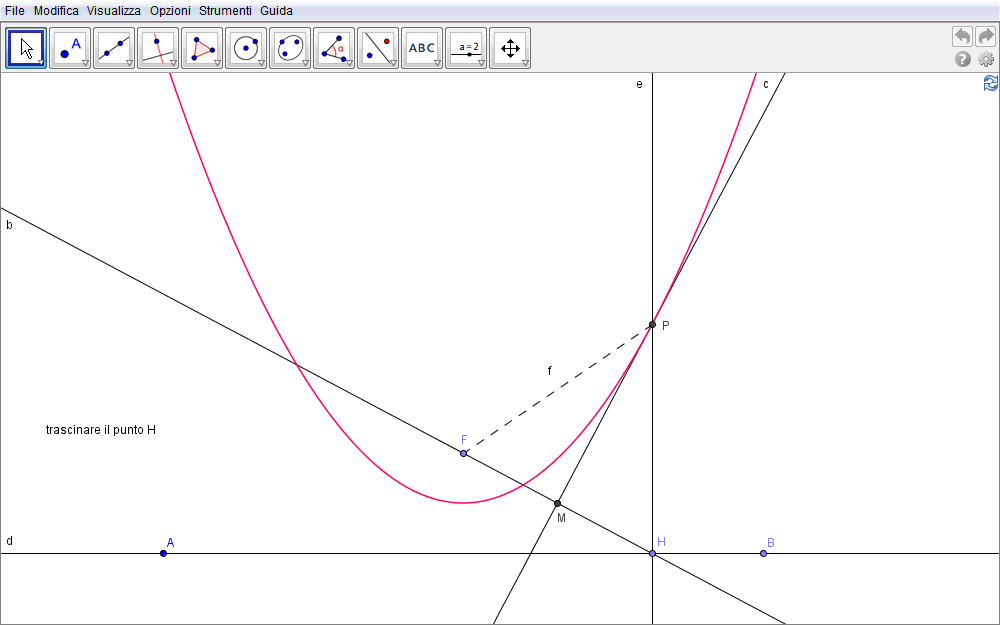
In riferimento alla figura sottostante
- sono assegnati una retta d (la direttrice, nella figura, orizzontale ottenuta come retta per i punti A e B) ed un punto F, il fuoco.
- Su tale retta si consideri un punto H qualsiasi e
- si tracci la retta FH.
- Individuato il punto medio M del segmento FH,
- si costruisca l'asse di FH.
- Costruita poi la retta per H perpendicolare alla direttrice d,
- questa incontra l'asse precedente in un punto P appartenente alla parabola.
Difatti
P, essendo equidistante da
H e
F perché appartenente all'asse del segmento con tali estremi, lo è pure dalla
retta
d e dal punto
F. Nella figura 1.1, trascinando il punto
H con il mouse (tasto
Muovi
![]() ) si fa
percorrere al punto
P l'arco di parabola cui appartiene (attivare con un clic destro sul punto
P la
Traccia attiva
) si fa
percorrere al punto
P l'arco di parabola cui appartiene (attivare con un clic destro sul punto
P la
Traccia attiva
![]() perché i punti
siano visibili). Per visualizzare il luogo selezionare il comando Luogo
perché i punti
siano visibili). Per visualizzare il luogo selezionare il comando Luogo
![]() .
.
Figura 1.1. parabola01.ggb.
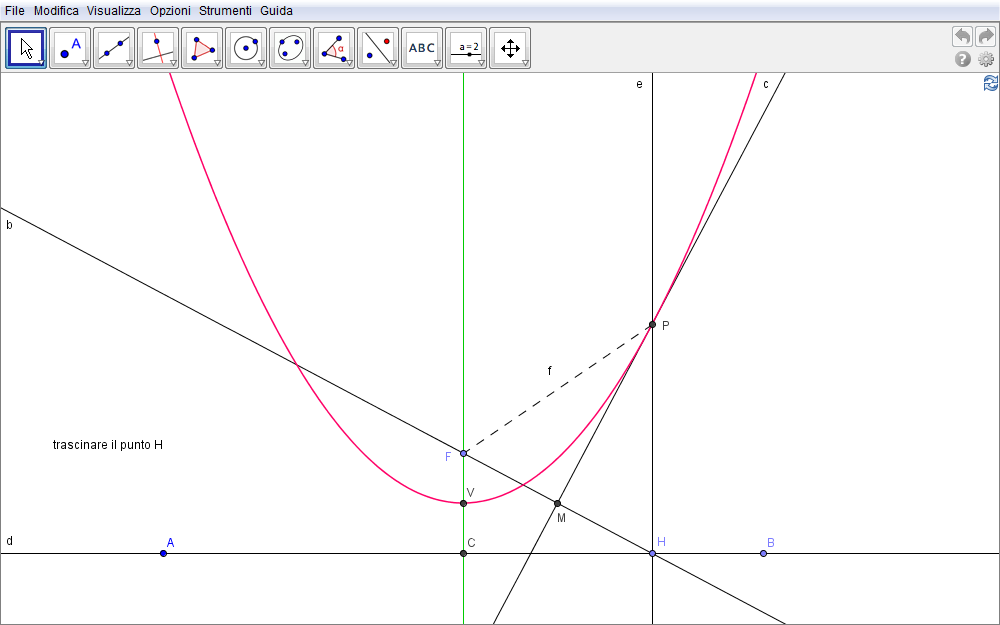
Appare evidente dalla costruzione come la parabola sia un insieme di punti simmetrico
rispetto ad una retta passante per il suo fuoco e perpendicolare alla direttrice. Tale
retta è detta
asse della parabola. Nella figura 1.2 che segue la si ottiene tracciando la
perpendicolare alla direttrice passante per il fuoco
F
![]() . In
tale configurazione il punto della parabola appartenente all'asse e punto medio del
segmento con estremi il piede C della perpendicolare condotta da
F alla direttrice ed
F stesso, è pure un punto importante e viene detto
vertice
V della parabola.
. In
tale configurazione il punto della parabola appartenente all'asse e punto medio del
segmento con estremi il piede C della perpendicolare condotta da
F alla direttrice ed
F stesso, è pure un punto importante e viene detto
vertice
V della parabola.
Figura 1.2. parabola02.ggb.
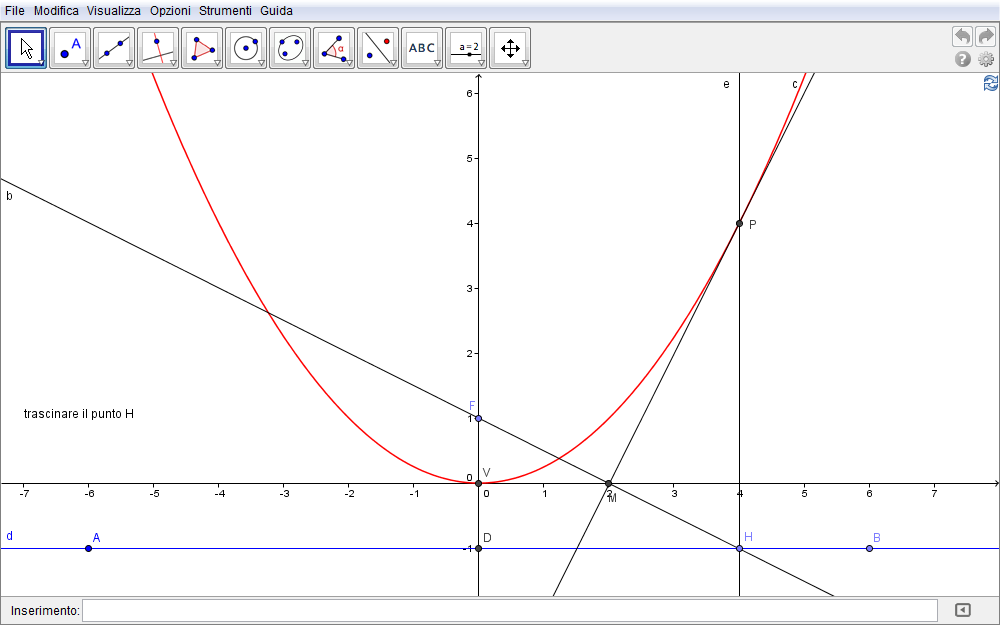
Se ora associamo alla retta passante per il vertice e parallela alla direttrice AB l'asse x di un sistema cartesiano, alla retta CF l'asse delle ordinate, il vertice V risulta in tal modo l'origine del sistema (fig. 1.3). Definite le coordinate del fuoco come \(F(0,f)\), l'equazione della direttrice è \(y=-f\) mentre le coordinate del punto P sono \(P(x,y)\), la condizione imposta dalla definizione geometrica \(PF=PH\) si traduce algebricamente in \begin{equation}PF=PH\quad\Rightarrow\quad \sqrt{(x-0)^2+(y-f)^2}=\bigl|y-(-f)\bigr|.\end{equation} Quadrando, riducendo i termini simili e dividendo per \(4 f\) otteniamo infine l'equazione \begin{equation}x^2+y^2+f^2-2fy=y^2+f^2+2fy \quad\Rightarrow\quad y=\biggl(\!{1\over 4f}\!\biggr)x^2\end{equation} che mostra una dipendenza quadratica dell'ordinata di P dalla sua ascissa. A conferma visiva di tale deduzione, nella fig. 1.3, la parabola è stata definita riportando nella barra di inserimento la sua equazione \(y=(1/4)\,x^2\) (si è scelto \(f=1\)) anziché, come nelle precedenti, ottenuta con il comando Luogo.
Figura 1.3. parabola03.ggb.