Iperbole: costruzione n. 2
La costruzione che proponiamo di seguito generalizza alcuni aspetti della precedente. Difatti anziché partire da una circonferenza ed un punto esterno,
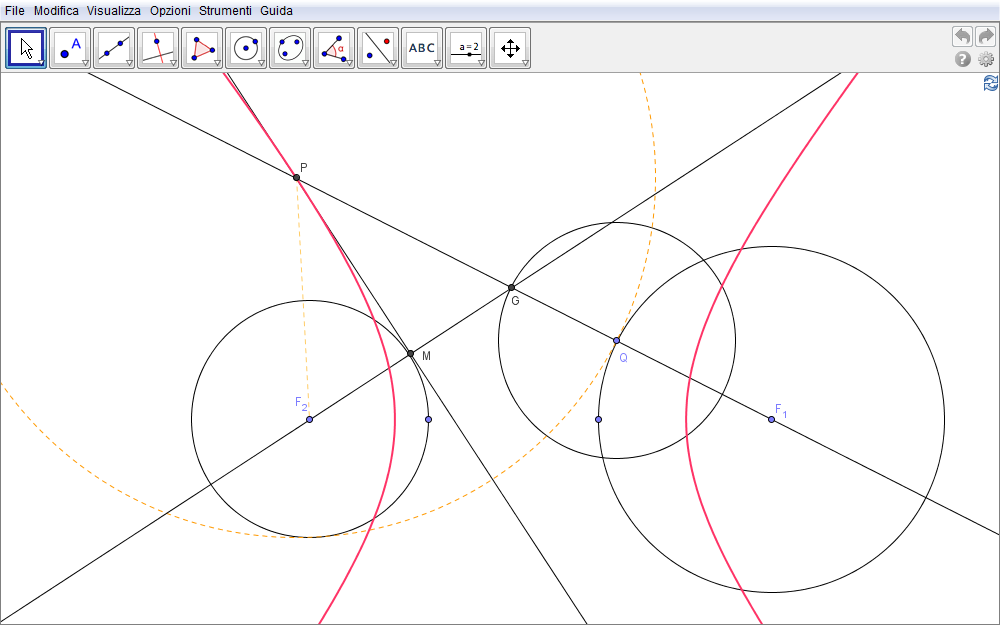
- costruiamo due circonferenze una esterna all'altra, di centri \(F_1\) e \(F_2\) e raggi, rispettivamente \(r_1\) e \(r_2\) (fig. 3.3).
- Preso ancora un qualsiasi punto Q della circonferenza di centro \(F_1\),
- tracciamo la circonferenza di centro Q e raggio \(r_2\).
- Il prolungamento del raggio \(F_1Q\) incontra quest'ultima circonferenza in G, punto esterno alla prima circonferenza.
- Individuato il punto medio M del segmento \(F_2G\),
- il suo asse incontra infine in P la retta \(F_1Q\).
Se ora tracciamo la circonferenza di centro P e raggio PQ notiamo che questa è tangente non solo alla prima circonferenza ma pure a quella di centro \(F_2\). Difatti l'appartenza di P all'asse del segmento \(F_2G\) assicura che \(PF_2=PG\) mentre la distanza massima di P dal punto più lontano della circonferenza di centro \(F_2\) è \(PF_2+r_2\). D'altra parte \begin{equation}PF_2+r_2=PG+r_2=PG+GQ=PQ\end{equation} che è appunto il raggio della circonferenza di centro P. Trascinando il punto Q nella figura 3.3 seguente è immediato notare l'appartenenza di P all'iperbole di fuochi \(F_1\) e \(F_2\).
Figura 3.3. iperbole03.ggb.
La dimostrazione di questa osservazione è altrettanto immediata: difatti, tenendo conto dell'uguaglianza \(PF_2=PG\), la differenza delle distanze di P dai fuochi risulta \begin{equation}PF_1-PF_2=(PG+GF_1)-PF_2=PG+GF_1-PF_2=GF_1=r_1+r_2\end{equation} ed essendo costante la somma dei raggi delle due circonferenza, P soddisfa alla definizione data di iperbole. Come detto inizialmente, questa costruzione generalizza la precedente: difatti quest'ultima si riduce alla precedente nel caso che il raggio della seconda (o alternativamente della prima) circonferenza si riduca a zero.
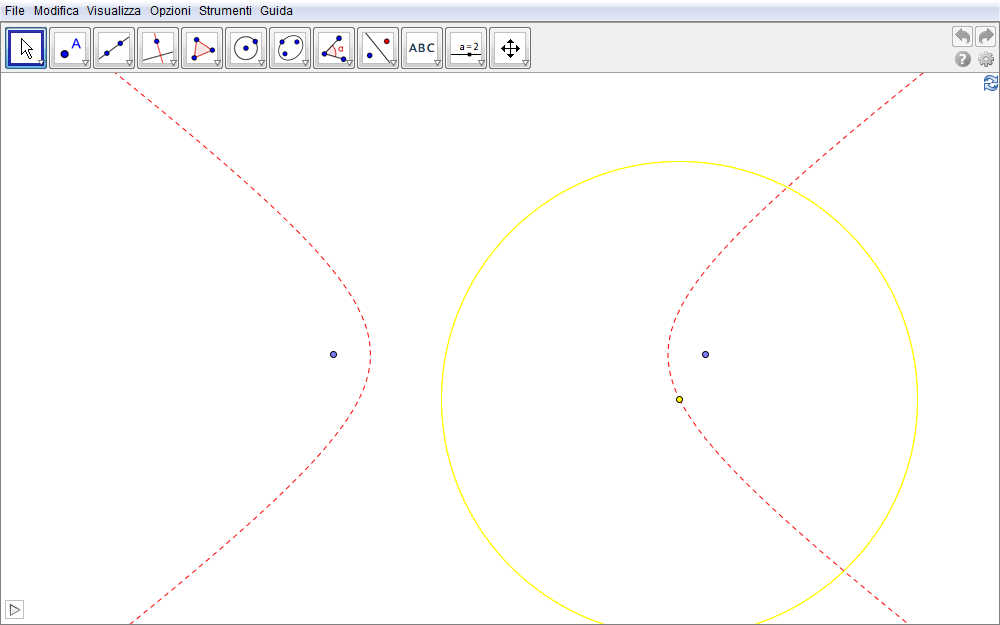
L'animazione seguente mostra in colore alcune circonferenze della famiglia di centro P e, nel medesimo colore, i corrispondenti centri.
Figura 3.4. iperbole04.ggb.