Iperbole: costruzione n. 1
Le costruzioni dell'iperbole seguono in genere quelle dell'ellisse con piccole ma sostanziali modifiche per cui, nel seguito, si ricalca in diversi punti quanto già esposto per l'ellisse. Dalla definizione di iperbole come il
luogo geometrico dei punti P del piano tali da avere costante il valore assoluto della differenza delle distanze da due punti fissi assegnati (i fuochi)
deriva la prima costruzione che proponiamo.
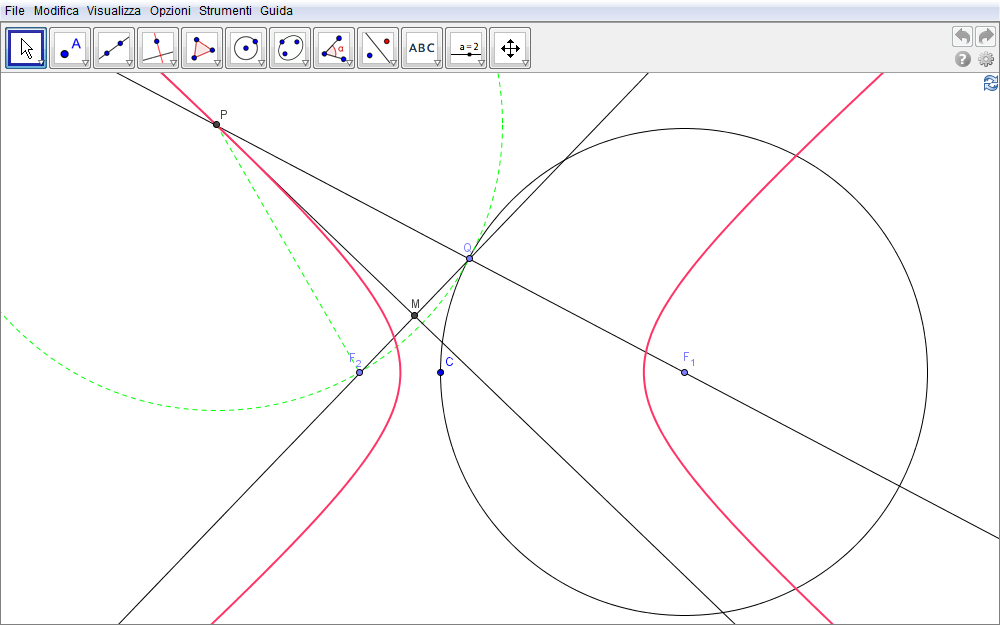
- Siano dati i due punti (i fuochi \(F_1\) e \(F_2\) nella figura 3.1) e sia \(2a\) la differenza (in valore assoluto) delle distanze da questi di un punto P dell'iperbole.
- Geometricamente identifichiamo tale valore con il raggio di una circonferenza centrata in uno di questi fuochi (\(F_1\) nell'animazione successiva). L'altro fuoco \(F_2\) dev'essere, diversamente che nell'ellisse, esterno a tale circonferenza.
- Consideriamo un punto qualsiasi Q della circonferenza centrata in \(F_1\) e
- tracciamo la retta che lo collega con il fuoco \(F_1\).
- Tracciamo poi la retta che collega questo punto con l'altro fuoco \(F_2\) e quindi
- costruiamo il punto medio M del segmento \(F_2Q\) definito da questi due punti.
- Costruita la retta asse del segmento \(F_2Q\),
- questa incontra la retta \(F_1Q\) in un punto P.
Figura 3.1. iperbole01.ggb.
Poiché questo punto appartiene all'asse del segmento \(F_2Q\)
risulta \(PF_2=PQ\) cosicché P soddisfa alla
proprietà \[PF_1-PF_2=PF_1-PQ=QF_1\]
ed evidentemente la differenza delle distanze di P dai due punti dati è quindi
pari al raggio scelto ossia è una costante al variare di Q su tale
circonferenza.
Il punto P appartenente all'iperbole è pure il centro della circonferenza passante,
- per il fuoco F2 e
- per il punto arbitrario Q, nonché
- tangente in Q alla circonferenza originaria in quanto P appartiene alla retta QF1.
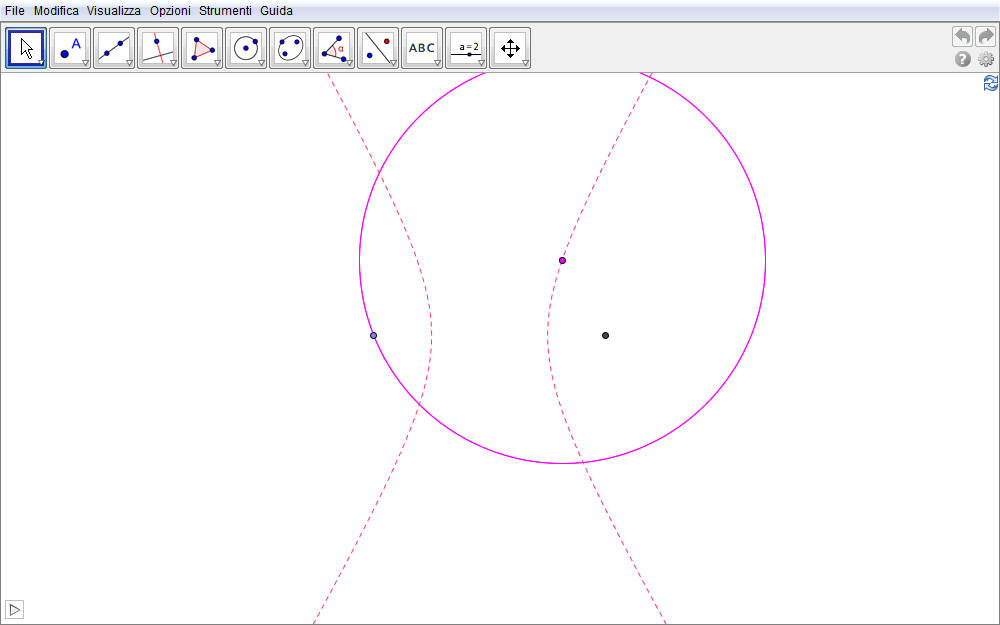
Per tale motivo l'iperbole si può interpretare quindi anche come il luogo dei centri della famiglia di circonferenze passanti per un punto esterno ad una data circonferenza e a questa tangente esternamente o internamente. Attivata l'animazione, la figura 3.2 seguente mostra alcune circonferenze di tale famiglia con i centri corrispondenti evidenziati nello stesso colore.
Figura 3.2. iperbole02.ggb.