Ellisse: costruzione n. 1
Richiamata la tradizionale definizione di ellisse:
luogo geometrico dei punti P del piano tali da avere la somma delle distanze da due punti fissi F1 e F2 (i fuochi) uguale ad una costante.
determiniamo con gli strumenti della geometria euclidea un punto che la soddisfi.
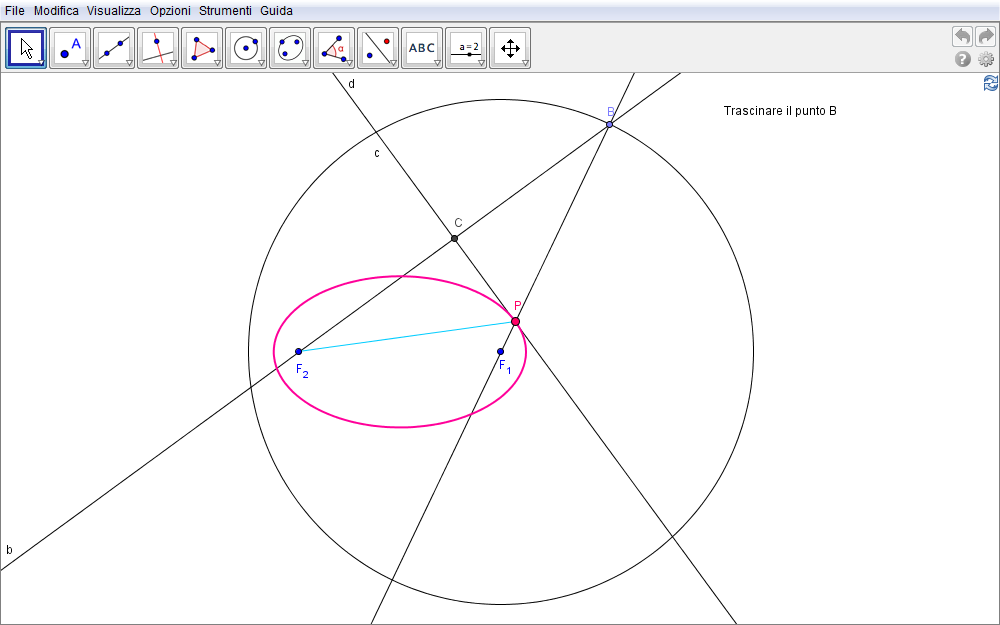
Figura 2.1. ellisse01.ggb.
Siano dati i due punti (i fuochi \(F_1\) e \(F_2\) nella figura 2.1) e sia 2a la somma delle distanze da questi di un punto P dell'ellisse \(PF_1+PF_2=2a\). La disuguaglianza triangolare applicata a \(\triangle F_1PF_2\) implica che sia \(PF_1+PF_2>F_1F_2\) per cui, se identifichiamo il valore \(2a\) con il raggio \(F_1A\) di una circonferenza centrata in uno di questi fuochi, per esempio \(F_1\), l'altro fuoco dovrà essere interno a tale circonferenza.
- Nascosto il punto A,
- consideriamo un punto qualsiasi B di tale circonferenza e
- tracciamo la retta che lo collega con il fuoco \(F_1\) scelto come centro.
- Possiamo ora tracciare la retta che collega questo punto con l'altro fuoco e quindi
- ottenere il punto medio C del segmento definito da questi due ultimi punti.
- Costruita la retta asse del segmento \(F_2B\),
- questa incontra il raggio \(F_1B\), tracciato inizialmente, in un punto P.
Poiché questo punto appartiene all'asse del segmento \(F_2B\) risulta \(PF_2=PB\) cosicché P soddisfa alla proprietà \begin{equation}PF_2+PF_1=PB+PF_1=F_1B\end{equation} per cui evidentemente la somma delle sue distanze dai due punti dati è pari al raggio scelto ossia è costante.
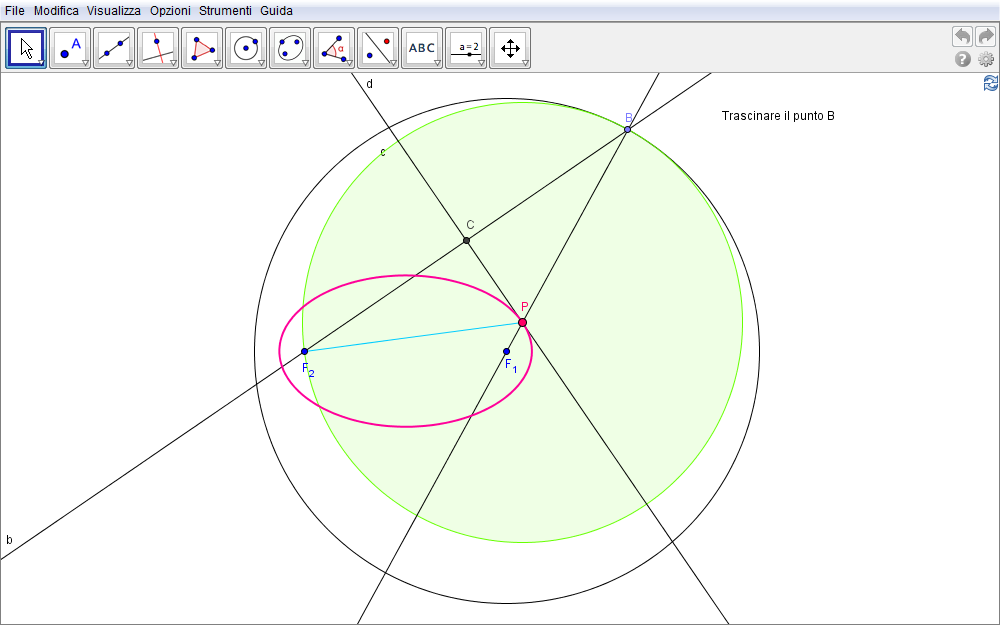
Poiché il punto P appartenente all'ellisse si può considerare come il centro della circonferenza passante per il fuoco \(F_2\), il punto arbitrario B e, in quanto P appartiene pure al raggio della circonferenza iniziale, tangente internamente a quest'ultima, l'ellisse si può interpretare anche come il luogo dei centri della famiglia di circonferenze passanti per un punto interno ad una data circonferenza e a questa tangente. La figura 2.2 seguente aggiunge alla precedente questo ulteriore elemento geometrico. Notiamo inoltre come la retta d, asse di \(F_2B\) sembri al variare di B sempre tangente all'ellisse.
Figura 2.2. ellisse02.ggb.
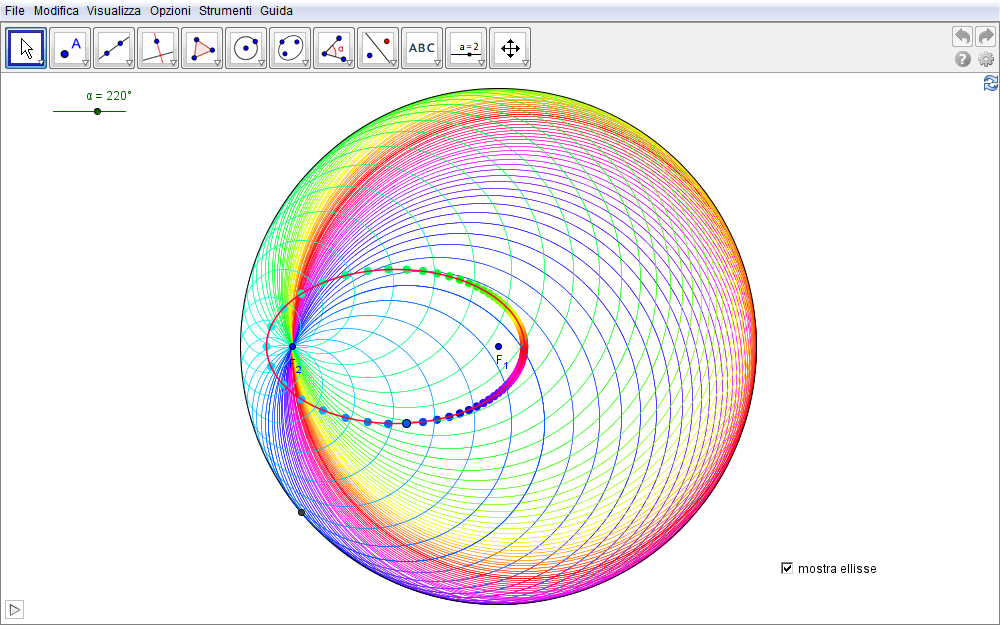
L'animazione sottostante (per avviarla in GeoGebra clic sulla freccia in basso a sinistra) traccia un certo numero di punti dell'ellisse ottenuti con la costruzione precedente ed inoltre rappresenta con il medesimo colore le circonferenze passanti per un fuoco, tangenti alla circonferenza originaria e aventi i punti dell'ellisse come centri. Un clic sulla casella in basso a destra per nascondere o mostrare il luogo percorso dal punto in colore.
Figura 2.3. ellisse03.ggb.