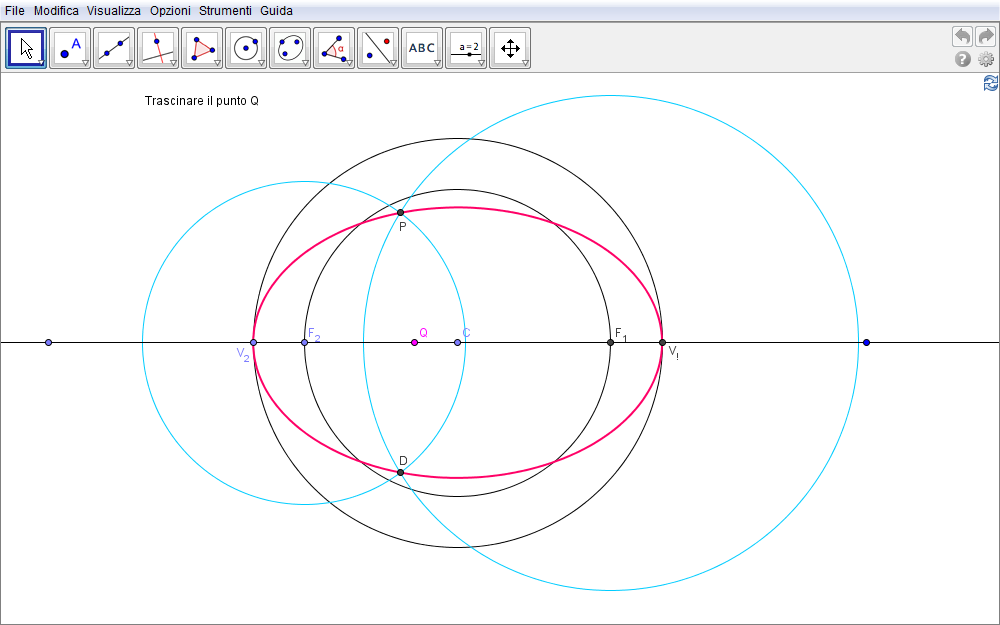
Ellisse: costruzione n. 4
- Il primo passo della costruzione consiste nel tracciare una retta e quindi,
- considerato un suo punto C,
- costruire una circonferenza avente un dato raggio.
- Questa incontra la retta in due punti, \(V_1\) e \(V_2\).
- Con lo stesso centro si tracci una seconda circonferenza di raggio inferiore alla precedente e siano
- \(F_1\) e \(F_2\) le sue intersezioni con il diametro \(V_1V_2\) della precedente.
- Sia Q un punto qualsiasi del diametro \(F_1F_2\).
- Si tracci ora la circonferenza di centro \(F_1\) e raggio pari alla lunghezza di \(V_1Q\)
 .
.
- Allo stesso modo si tracci la circonferenza di centro \(F_2\) e raggio \(V_2Q\).
Figura 2.11. ellisse11.ggb.
Evidentemente i punti P e D di intersezione di queste ultime due circonferenze sono simmetrici rispetto alla retta iniziale e distano da \(F_1\) una distanza pari a \(V_1Q\) e da \(F_2\) la lunghezza di \(V_2Q\) cosicché la loro somma è costante e pari a \(V_1V_2\). Tali punti appartengono quindi ad una ellisse. Al variare del punto Q sul segmento \(F_1F_2\) si ottiene l'ellisse cercata.
Deduzione analitica
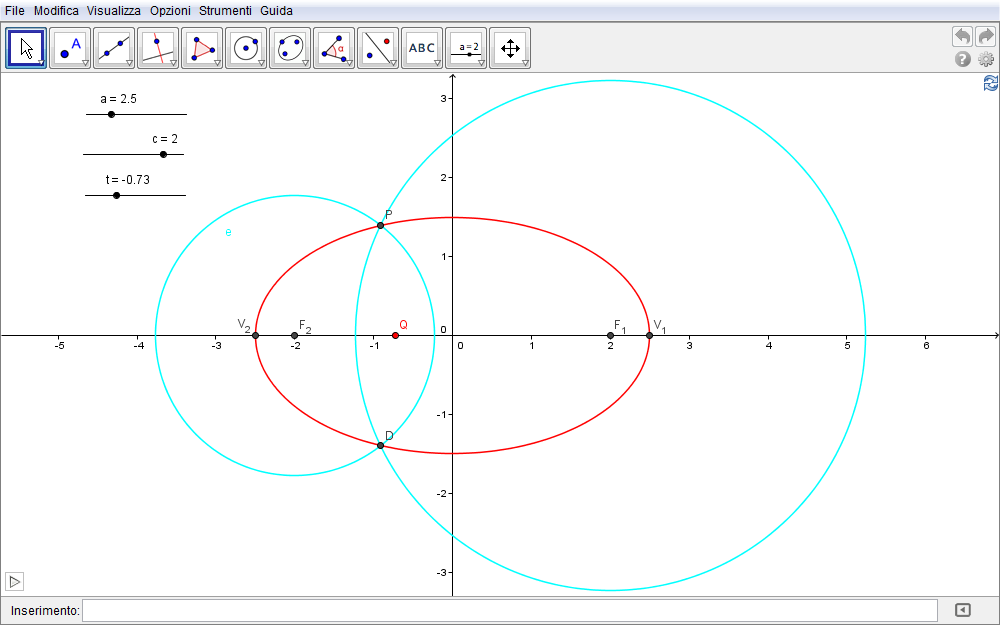
In questa sezione intendiamo riprodurre la precedente costruzione nelle forme della geometria analitica associando ai parametri della costruzione opportuni slider e immettendo i vari elementi geometrici e algebrici dalla barra di inserimento di GeoGebra. Pertanto, introdotto un sistema cartesiano, lo slider a, variabile tra 0 e 10, determina le ascisse dei vertici \(V_1(a,0)\) e di \(V_2(-a,0)\). Analogamente lo slider c, variabile tra 0 e a, definirà i fuochi \(F_1(c,0)\), \(F_2(-c,0)\). Infine allo slider t associamo l'ascissa del punto \(Q\) ossia \(Q(t,0)\) variabile tra gli estremi \(-c\leq t\leq c\). Tutti questi quattro punti sono inseriti in GeoGebra tramite la barra di inserimento (fig. 2.12).
Figura 2.12. ellisse12.ggb.
L'equazione della circonferenza di centro \(F_1\) e raggio \(V_1Q=a-t\) è allora \begin{equation}d:(x-c)^2+y^2=(a-t)^2\end{equation} mentre quella di centro \(F_2\) e raggio \(V_2Q=t-(-a)=t+a\) risulta \begin{equation}e:(x+c)^2+y^2=(t+a)^2.\end{equation} Per determinare i loro punti di intersezione, P e D, dobbiamo evidentemente risolvere il sistema (di II grado) \begin{equation}\cases{(x-c)^2+y^2=(a-t)^2\cr (x+c)^2+y^2=(t+a)^2\cr}\quad\Rightarrow\quad \cases{x^2+c^2-2cx+y^2=a^2+t^2-2at\cr x^2+c^2+2cx+y^2=a^2+t^2+2at.\cr}\end{equation} Moltiplicando per \(-1\) la prima e sommando in colonna, si ha facilmente \begin{equation}4xc=4at\quad\Rightarrow\quad x={at\over c}.\label{eq:4}\end{equation} Introdotto quest'ultimo risultato nella prima equazione \begin{equation}{a^2t^2\over c^2}+c^2-2c\cdot {at\over c}+y^2=a^2+t^2-2at\quad\Rightarrow\quad {a^2t^2\over c^2}+c^2-2at+y^2=a^2+t^2-2at\end{equation} si giunge dopo qualche semplificazione algebrica all'equazione \begin{equation}y^2={(a^2-c^2)(c^2-t^2)\over c^2}\label{eq:6}\end{equation} che, date le limitazioni poste \(a\geq c\) e \(t\in[-c,c]\), fornisce le due soluzioni \begin{equation}y=\pm{\sqrt{(a^2-c^2)(c^2-t^2)}\over c}.\end{equation} I punti P e D (fig. 2.12) hanno quindi coordinate \begin{equation}P\biggl({at\over c},{\sqrt{(a^2-c^2)(c^2-t^2)}\over c}\biggr),\qquad D\biggl({at\over c},-{\sqrt{(a^2-c^2)(c^2-t^2)}\over c}\biggr)\end{equation}
Immesse queste espressioni in GeoGebra, per completare questa traduzione analitica manca la deduzione dell'equazione dell'ellisse. A tale scopo riprendiamo i risultati \eqref{eq:4} e \eqref{eq:6} \begin{equation}\cases{x={at\over c}\cr \cr y^2={(a^2-c^2)(c^2-t^2)\over c^2}.\cr}\end{equation} Tale coppia di equazioni esprime l'ascissa e il quadrato dell'ordinata dei punti dell'ellisse in termini del parametro \(t\). Siamo quindi di fronte ad una rappresentazione parametrica di tale curva e pertanto, per ottenere la classica rappresentazione implicita, dovremo eliminare la dipendenza da \(t\). Dalla prima equazione segue quindi \(t=(cx)\,/a\) cosicché la seconda diviene \begin{equation}y^2={(a^2-c^2)(c^2-c^2x^2/a^2)\over c^2}\end{equation} che si semplifica in \begin{equation}y^2=(a^2-c^2)\biggl(1-{x^2\over a^2}\biggr).\end{equation} Se dividiamo per \(a^2-c^2\) otteniamo infine \begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}+{y^2\over a^2-c^2}=1}\end{equation} che è l'equazione del luogo da immettere in GeoGebra: avviare l'animazione in fig. 2.12 per verificare l'appartenenza dei punti all'ellisse. Infine se poniamo \(b^2=a^2-c^2\) l'equazione precedente assume la già nota forma canonica.