Ellisse: costruzione n. 2
La costruzione che proponiamo di seguito generalizza alcuni aspetti della precedente. Difatti anziché partire da una circonferenza e un punto interno,
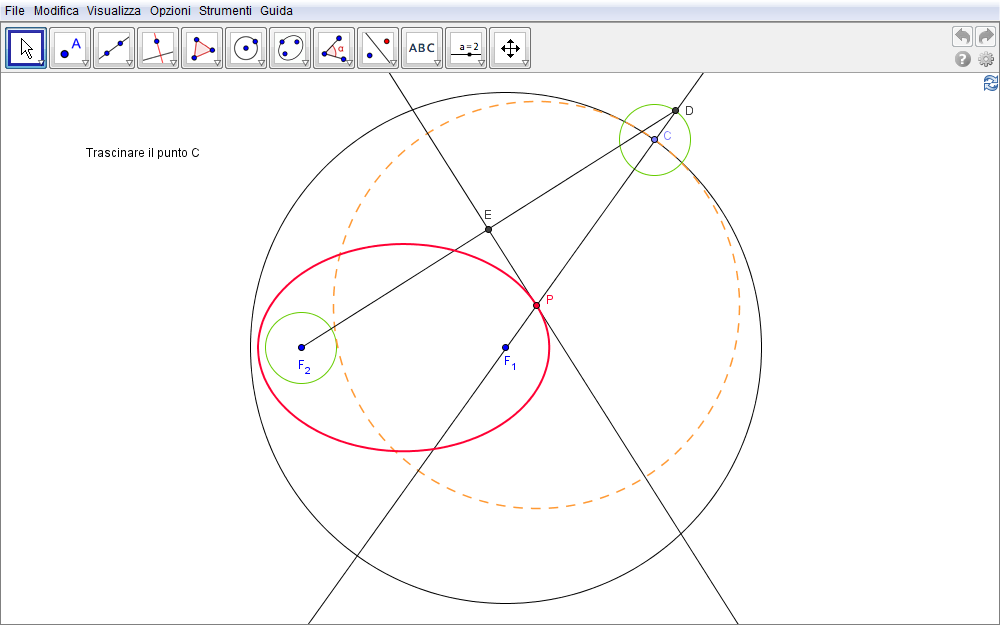
- costruiamo due circonferenze una interna all'altra, di centri \(F_1\) e \(F_2\) e raggi, rispettivamente \(r_1\) e \(r_2\) con \(r_1>r_2\) (in fig. 2.4 i punti A e B serviti per definire i raggi sono stati nascosti).
- Preso ancora un qualsiasi punto C della circonferenza di raggio maggiore,
- tracciamo la circonferenza di centro C e raggio \(r_2\).
- La retta \(F_1C\) incontra quest'ultima circonferenza in D, punto esterno alla prima circonferenza.
- Individuato il punto medio E del segmento \(F_2D\),
- il suo asse interseca infine in P il raggio \(F_1C\).
- Se ora tracciamo la circonferenza di centro P e raggio PC (in tratteggio nella figura) notiamo che questa è tangente non solo alla prima circonferenza ma pure a quella di centro \(F_2\).
Difatti l'appartenza di P all'asse del segmento \(F_2D\) assicura che \(PF_2=PD\) dalla quale si ha che la distanza \(PF_2-r_2\) di P da un qualsiasi punto della circonferenza di centro \(F_2\) è \begin{equation}PF_2-r_2=PD-r_2=PD-CD=PC\end{equation} che è appunto il raggio della circonferenza di centro P. Trascinando il punto C sulla circonferenza di raggio maggiore appare evidente come P giaccia su una ellisse avente \(F_1\) e \(F_2\) come fuochi.
Figura 2.4. ellisse04.ggb.
La dimostrazione di questa osservazione è immediata: difatti, tenendo conto che \(PF_2=PD\), la somma delle distanze di P dai fuochi risulta \begin{equation}PF_1+PF_2=PF_1+PD=F_1D=r_1+r_2\end{equation} ed essendo costante la somma dei due raggi, P soddisfa alla definizione data di ellisse.
Come detto inizialmente questa costruzione generalizza la precedente in quanto quest'ultima si riduce alla precedente nel caso che il raggio della seconda circonferenza si riduca a zero.
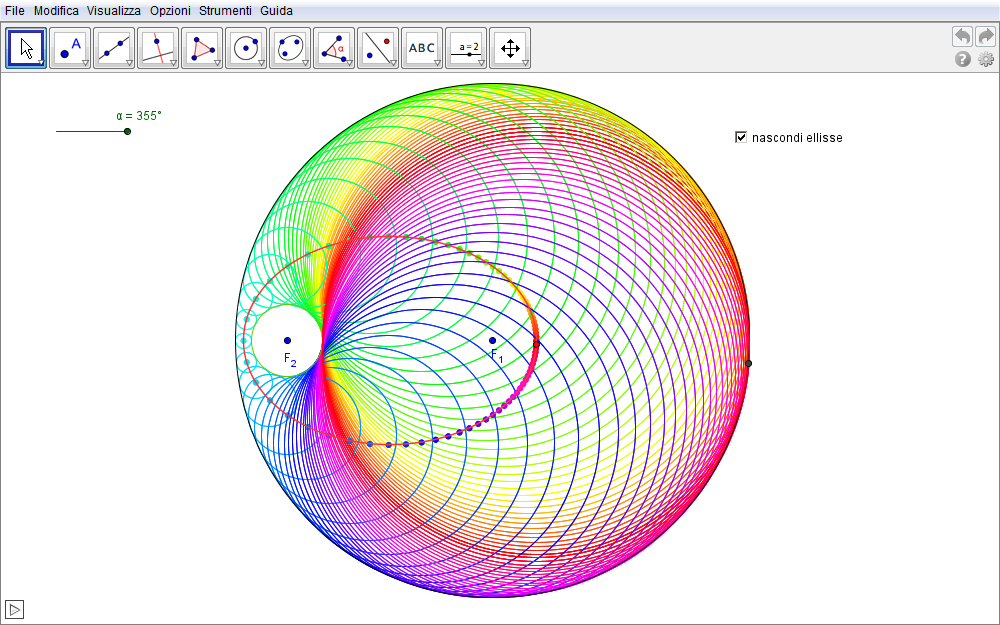
La figura seguente associa con lo stesso colore punti dell'ellisse con le circonferenze che hanno questi stessi punti come centri.
Figura 2.5. ellisse05.ggb.
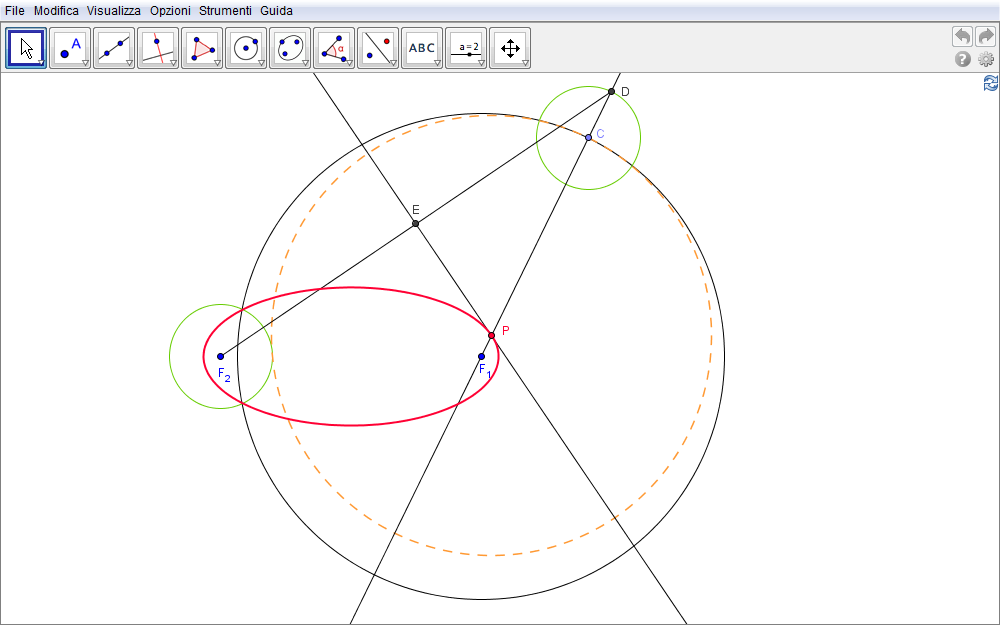
Variando la distanza tra i fuochi osserviamo che la costruzione rimane valida anche quando il centro della seconda circonferenza è esterno alla prima (fig. 2.6): è necessario comunque che queste abbiano dei punti di intersezione altrimenti il luogo dei centri delle circonferenze tangenti alle due date cambia completamente.
Figura 2.6. ellisse06.ggb.
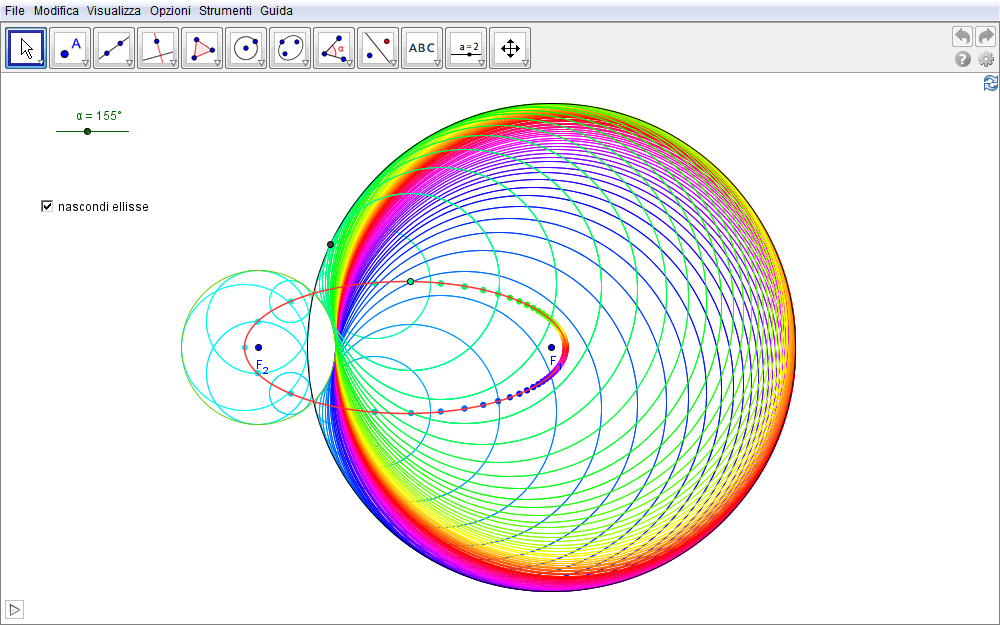
Infine, la figura sottostante mostra alcuni punti dell'ellisse e le corrispondenti circonferenze aventi questi come centri. Come detto inizialmente, queste ultime sono sempre tangenti alle circonferenze di centri \(F_1\) e \(F_2\).
Figura 2.7. ellisse07.ggb.