
Ritorna alla pagina di presentazione

Elementi di...arcobaleno
Dedicato a coloro che, guardandolo, ancora si meravigliano.
Lorenzo Roi
(dicembre 2010)
Introduzione

Foto 1. Arcobaleno completo (http://it.wikipedia.org/wiki/Arcobaleno).
Osservazioni iniziali
Tutti noi sappiamo che cos'è l'arcobaleno: l'arco che lo forma e i colori che manifesta sono uno spettacolo che, pur effimero, da sempre attrae e affascina. L'esperienza ci suggerisce che tale fenomeno si manifesta in alcune situazioni particolari specie dopo una pioggia quando riappare la luce solare e le nuvole temporalesche si trovano dalla parte opposta al sole. Anche i colori dell'arcobaleno ci sono familiari ma, probabilmente, non per averli effettivamente colti nell'arcobaleno ma per averli associati, già dai primi anni di scuola, alla classica sequenza costituita dal rosso, arancione, giallo, verde, blu, indaco e violetto, introdotta da Newton allo scopo di suddividere lo spettro dei colori visibili in sette classi in analogia con le sette note musicali.
Per una spiegazione scientifica esauriente di tale fenomeno naturale si richiedono conoscenze fisiche e matematiche avanzate ma già un approccio che sfrutti principalmente le leggi dell'ottica geometrica ossia le semplici leggi della riflessione e della rifrazione (ritenute dei prerequisiti per la lettura di questo scritto), dà conto delle sue principali caratteristiche. In quanto segue ci si propone di spiegare le caratteristiche essenziali dell'arcobaleno per poterle riconoscere con consapevolezza durante il fenomeno e secondariamente, almeno accennare, ad altre meno conosciute peculiarità.
All'approccio geometrico classico associamo un certo numero di inserti, interattivi per chi possiede Mathematica (versione 7 o successive). In quest’ultimo caso si potrà sperimentare con il file notebook (arcobaleno.nb) dal quale si è tratta questa pagina HTML.
Sole e pioggia
Un arcobaleno si può osservare solo in situazioni particolari: ci si deve comunque trovare tra il sole e, dalla parte opposta, vi deve essere una regione del cielo ancora investita dalla pioggia. Il sole, come vedremo, dev'essere sufficientemente basso all'orizzonte. L'arcobaleno appare sempre dalla parte opposta ai raggi solari per cui, rivolto all'arcobaleno, l'osservatore ha sempre alle spalle il sole. Arcobaleni si possono osservare anche in vicinanza delle cascate o si possono generare con relativa facilità in giardino con uno spruzzo d'acqua disposto dalla parte opposta al sole. In tutte queste situazioni vengono coinvolte gocce d'acqua colpite dai raggi solari ed è pertanto su queste che ci si deve concentrare per spiegarne il meccanismo.
Consideriamo una goccia d'acqua di indice di rifrazione pari a n = 4/3 (nei calcoli numerici sarà questo il valore standard per l'indice di rifrazione che, fino ad un certo punto, associeremo alle gocce) colpita da un raggio di luce monocromatico cioè di un'unica lunghezza d'onda. Se il raggio della goccia è inferiore al millimetro la forma della goccia sospesa in aria è praticamente una sfera perfetta in quanto la forza di gravità non riesce a deformarla vincendo le forze di tensione superficiale. Consideriamo quindi gocce di tale forma: il raggio sarà nella nostra analisi un parametro ininfluente per cui potremo considerarlo, per comodità, unitario. (Nelle funzioni utilizzate per il calcolo tale parametro è introdotto principalmente per motivi di controllo dimensionale).
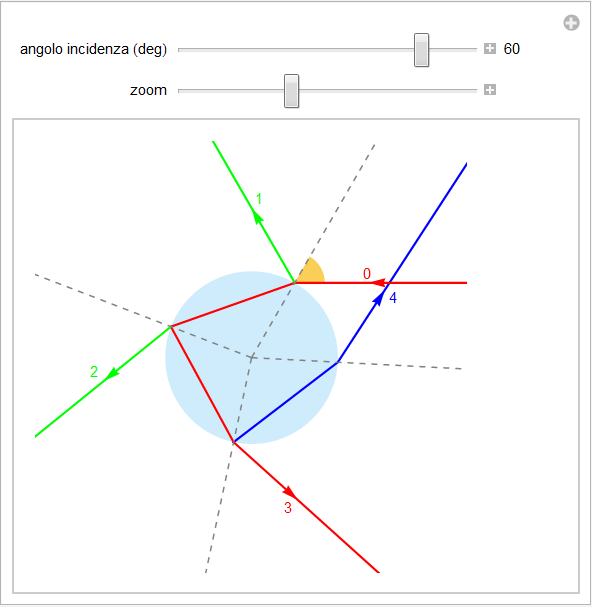
Figura 1. Percorsi di un raggio di luce in una goccia d'acqua.
In riferimento alla figura 1 analizziamo i fenomeni cui è soggetto un raggio di luce incidente sulla goccia e i percorsi che ne derivano. Se quindi indichiamo con il numero 0 il raggio incidente (colore rosso), l'angolo con cui esso incide appare nella figura in colore arancio (le linee tratteggiate indicano le normali nei diversi punti di incidenza). Nel punto di incidenza aria/acqua il raggio incidente si suddivide in un raggio riflesso (verde, identificato dal n. 1) e in uno rifratto (rosso). Questo incide poi sulla parete posteriore della goccia e subisce un'ulteriore suddivisione in uno riflesso internamente (rosso) e in un raggio rifratto (verde, n. 2). Il raggio interno riflesso incide nuovamente dall'interno sulla superficie della goccia e, per la seconda volta, viene separato in un raggio riflesso internamente (blu) e in un raggio rifratto (rosso, n. 3). Ovviamente ad ogni riflessione/rifrazione l'intensità luminosa diminuisce ma tale fatto sarà da noi trascurato. Il raggio riflesso internamente già due volte (rosso/blu) procede con un terzo contatto con la superficie di separazione acqua/aria ed emerge, per rifrazione, un ulteriore raggio (blu, n. 4). Si può ulteriormente procedere con tale successione ma, come vedremo, già i raggi 3 e 4 permetteranno di spiegare adeguatamente e nei limiti che ci siamo dati, le principali caratteristiche dell'arcobaleno.
Arcobaleno primario
Diffusione di un raggio luminoso monocromatico
In questa sezione intendiamo studiare nello specifico la geometria che si accompagna al percorso evidenziato in rosso nella immagine precedente (figura 1) ossia si vuole approfondire il comportamento di un raggio monocromatico che subisce internamente alla goccia una sola riflessione emergendo quindi diffuso ad un certo angolo nella successiva rifrazione (rosso, n. 3). In particolare, dedurremo la deviazione subita da un raggio incidente al variare dell'angolo di incidenza fornendo poi il grafico del suo angolo supplementare.
Sia quindi n l'indice di rifrazione dell'acqua e indicati con i l'angolo di incidenza e con r l'angolo di rifrazione, la legge della rifrazione
| (1) |
permette di esprimere l'angolo di rifrazione r in termini dell'angolo di incidenza ossia
| (2) |
da cui, passando alla funzione inversa, abbiamo
| (3) |
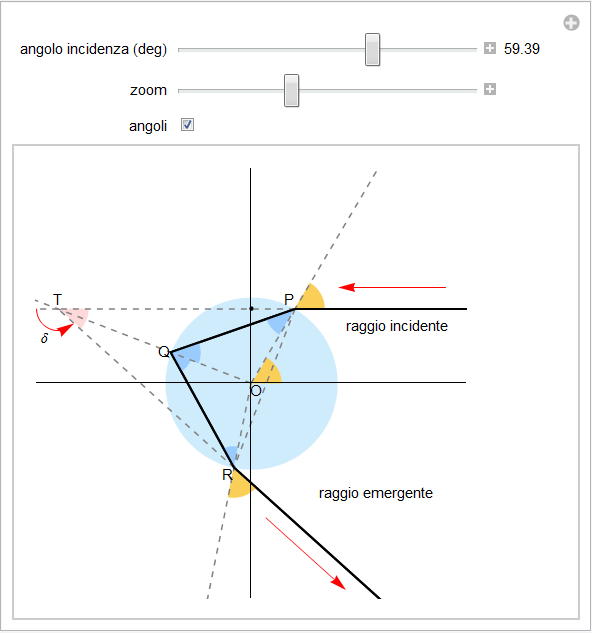
Figura 2. Percorso di un raggio incidente ed angolo di deviazione.
In base alla figura 2 che rappresenta una goccia d'acqua sferica in sezione assieme agli angoli coinvolti, ricaviamo la deviazione δ subita da un raggio incidente e che emerge dopo una sola riflessione interna. Possiamo procedere in diversi modi il primo dei quali fa uso della geometria del triangolo mentre il secondo tratta delle singole deviazioni.
a) Notiamo innanzitutto che i triangoli OPQ e OQR sono uguali, isosceli, con angoli alla base pari a r (in blu nella figura 2) mentre gli angoli al vertice misurano ∠POQ = ∠QOR = π - 2r. Inoltre poiché nella rifrazione che avviene nel punto R l'angolo di incidenza è pari ad r mentre quello di rifrazione è i si ha pure
| (4) |
Quindi pure i triangoli OPT e ORT sono uguali avendo due angoli e il lato compreso uguali e, pertanto, △PTR è isoscele con altezza e bisettrice la retta OT. Definita la deviazione δ del raggio emergente rispetto alla direzione originaria, quest'angolo appare essere adiacente esterno all'angolo al vertice di △PTR per cui
| (5) |
Essendo ∠OQP =∠PTQ +∠QPT in quanto angolo adiacente esterno, la precedente diviene
| (6) |
e quindi, sostituendo i valori già discussi ∠OQP = r e ∠QPT = i - r, si ha in definitiva
| (7) |
Dalla geometria della precedente figura si ricava facilmente che il cosiddetto angolo di diffusione α, ossia l'angolo acuto formato dal raggio incidente e dal raggio diffuso verso l'osservatore, osservatore che immaginiamo posizionato sempre in basso e a destra rispetto alla goccia, (α è evidenziato in rosa nelle figure 2 o 3) è collegato all'angolo di incidenza i e a quello di rifrazione r dalla importante relazione
| (8) |
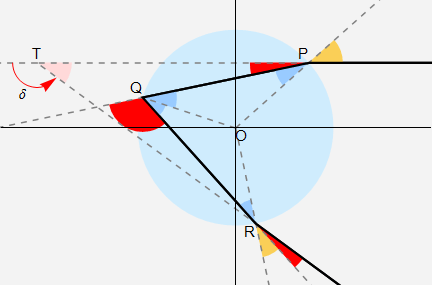
Figura 3. Singole deviazioni e angolo di diffusione.
b) Un metodo alternativo per giungere a tale risultato consiste nel valutare la deviazione totale δ come somma delle tre deviazioni (figura 3, in rosso) subite dal raggio incidente nel suo percorso complessivo. Risulta che
nella prima rifrazione la deviazione ![]() è pari a
è pari a ![]() ,
,
nella prima riflessione interna ![]() ,
,
nella seconda rifrazione è ancora ![]() ,
,
da cui si ottiene ancora
| (9) |
e quindi ritroviamo il risultato già dedotto per l'angolo di diffusione α.
Importanza dell'angolo di diffusione
Per capire l'importanza dell'angolo di diffusione conviene rappresentare la situazione nella quale viene a trovarsi un osservatore quando è disposto tra il sole ed una regione nella quale vi sia uno numero sufficiente di gocce d'acqua colpite dai raggi solari (figura 4).
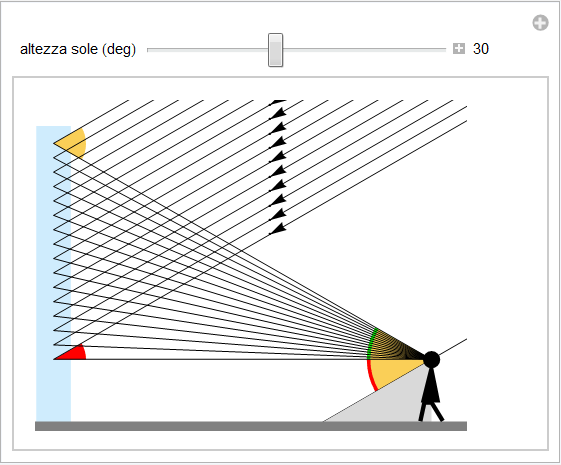
Figura 4. Angoli di diffusione delle gocce d'acqua.
I raggi solari incidono parallelamente sullo strato verticale di pioggia (in azzurro nella figura 4), vengono parzialmente diffusi all'indietro con angoli di diffusione diversi a seconda della loro posizione e quindi convergono verso l'osservatore. Questi coglierà la luce diffusa da tale regione entro un certo intervallo angolare i cui estremi si possono individuare una volta definiti alcuni elementi di carattere geometrico. Consideriamo perciò
1. il raggio solare che passa per l'osservatore e che proietta poi l'ombra dell'osservatore stesso sul terreno: il punto opposto al sole che in tal modo si individua al suolo è detto punto antisolare: è rispetto a tale direzione che successivamente rileveremo le dimensioni angolari dell'arcobaleno.
2. i raggi diffusi dalle gocce di pioggia che si trovano appena sopra l'orizzonte e che convergono all'osservatore parallelamente al terreno. Infine
3. i raggi solari diffusi verso l'osservatore e provenienti dalle gocce che stanno nella parte superiore della regione investita dalla pioggia.
L'angolo di diffusione per le gocce in prossimità del suolo è evidentemente pari all'altezza angolare hsole del sole sull'orizzonte (evidenziata in rosso nella figura 4) e questo valore è pure il valore minimo dell'angolo (arancio con margine rosso in figura 4) definito dal punto antisolare e dai raggi diffusi che convergono all'osservatore parallelamente al terreno e provenienti dalla zona inferiore dello strato di pioggia.
Se invece consideriamo le gocce che stanno nella parte superiore di tale regione, il loro angolo di diffusione (in arancio nella figura 4) coincide ancora con l'angolo che l'osservatore rileva tra il punto antisolare e la luce proveniente da tale zona (arancio con margini verde e rosso) ma in quest'ultimo caso tale valore è la somma dell'altezza hsole del sole (arancio con margine rosso) con l'altezza rispetto all'orizzonte della zona stessa (arancio con margine verde nella figura 4). Evidentemente tale angolo, che individuiamo come ![]() , dipende dalla distanza dell'osservatore dalla regione investita dalla pioggia e dalla sua elevazione ma è comunque sempre maggiore dell'altezza del sole sull'orizzonte.
, dipende dalla distanza dell'osservatore dalla regione investita dalla pioggia e dalla sua elevazione ma è comunque sempre maggiore dell'altezza del sole sull'orizzonte.
Poiché, come vedremo, l’angolo di formazione dell'arcobaleno rispetto al punto antisolare è costante (per un dato colore o lunghezza d’onda) ciò ci permetterà di comprendere perché l'arcobaleno si può osservare solo quando l'altezza del sole sull’orizzonte assume determinati valori.
In definitiva la regione investita dalla pioggia diffonde verso l'osservatore dei raggi solari ad angoli θ che soddisfano la disuguaglianza
| (10) |
essendo ![]() un valore certamente maggiore dell'altezza hsole del sole sull'orizzonte.
un valore certamente maggiore dell'altezza hsole del sole sull'orizzonte.
Angolo di arcobaleno e addensamento dei raggi emergenti
Sostituendo nella (8) l'angolo di rifrazione r espresso dalla (3), possiamo studiare l'andamento dell'angolo di diffusione al variare dell'angolo di incidenza i. Si ottiene la funzione α(i)
| (11) |
Per i valori di i ∈ [0°,90°], α(i) possiede il grafico di figura 5 e da tale rappresentazione emerge come gli angoli "permessi" per la diffusione appartengano ad un intervallo ben definito.
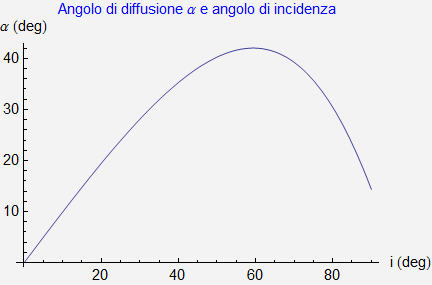
Figura 5. Grafico degli angoli di diffusione al variare dell'angolo di incidenza.
In particolare gli angoli permessi appartengono all'intervallo compreso tra 0°, e in tal caso il raggio viene diffuso all'indietro verso il sole, e un valore massimo che, relativamente all'indice di rifrazione n = 4/3, risulta essere approssimativamente di ![]() e corrisponde ad un angolo di incidenza i di circa 60°.
e corrisponde ad un angolo di incidenza i di circa 60°.
Un andamento analogo si ottiene se si sostituisce all'angolo di incidenza il parametro d'impatto y, grandezza che ci sarà utile per studiare la distribuzione in intensità dei raggi luminosi. Tale grandezza esprime la distanza del raggio incidente dal centro della goccia e, geometricamente, è l'ordinata del punto P nella figura 2 una volta che la goccia sia rappresentata da un cerchio di raggio R centrato nell'origine di un sistema cartesiano. Se R è il raggio della goccia, tale parametro potrà variare nell'intervallo [-R, R]. Il legame tra y e l'angolo i è dato in tale sistema dalla relazione y = R sen(i) per cui l'angolo di diffusione primario risulta espresso in termini di y dalla funzione
| (12) |
Il grafico, per y ∈ [0, R] con R = 1, è rappresentato in colore nella parte destra della figura 6. L'animazione da cui la figura è tratta permette, al variare del parametro d'impatto, di associare il corrispondente angolo di diffusione emergente dalla goccia. Difatti variando il parametro y in intorni del valore 0.86 in corrispondenza del quale α(y) raggiunge il valore massimo ossia studiando i raggi incidenti sulla goccia prossimi a tale valore, si può intuire come i corrispondenti raggi emergenti si addensino attorno al massimo della curva che risulta, come detto, un valore prossimo ai 42°.
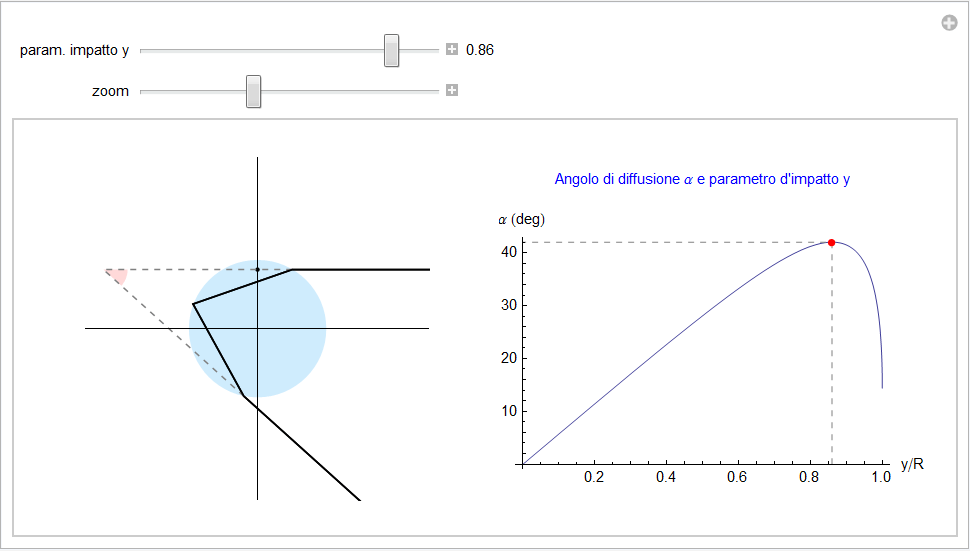
Figura 6. Angolo di diffusione e parametro d'impatto. Situazione geometrica.
Queste osservazioni qualitative si possono tradurre ulteriormente in forma grafica se si rappresenta l'intensità uniforme dei raggi incidenti sulla goccia come un insieme di linee egualmente spaziate nell'intervallo [0, R]: la corrispondente distribuzione dei raggi emergenti appare quindi graficamente in ordinata (figura 7).
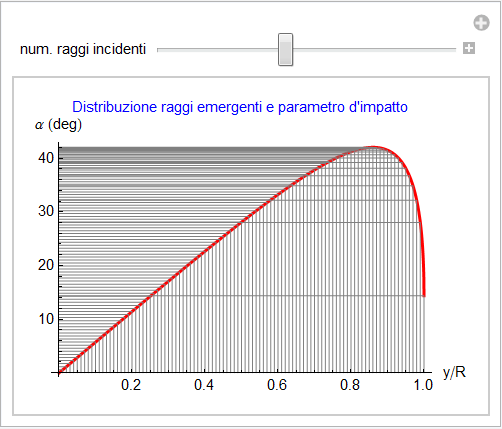
Figura 7. Distribuzione dei raggi emergenti e loro addensamento attorno all'angolo di arcobaleno.
Appare ora più evidente l'addensamento dei raggi attorno al valore massimo della curva in questione. Il valore di y (che indicheremo con ![]() , y critico) in corrispondenza del quale viene raggiunto il massimo si può determinare con i metodi dell'Analisi Matematica e risulta
, y critico) in corrispondenza del quale viene raggiunto il massimo si può determinare con i metodi dell'Analisi Matematica e risulta
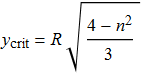 |
(13) |
per cui nel caso sia n = 4/3 ed R = 1, si ottiene
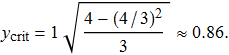 |
(14) |
L'angolo in corrispondenza del quale si ha la massima intensità luminosa per i raggi emergenti, angolo che definiamo come angolo di arcobaleno primario ![]() o, più brevemente, angolo di arcobaleno, si deduce sostituendo tale valore nella funzione α espressa dalla (12) e risulta
o, più brevemente, angolo di arcobaleno, si deduce sostituendo tale valore nella funzione α espressa dalla (12) e risulta
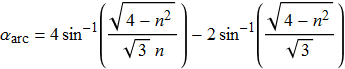 |
(15) |
Quest'ultimo risultato mostra una dipendenza dal solo indice di rifrazione mentre è indipendente dal raggio della goccia: gocce con raggio diverso diffondono i raggi solari responsabili dell'arcobaleno primario nello stesso modo. L'angolo di arcobaleno relativo all'indice di rifrazione n = 4/3, è quindi pari a
| (16) |
In conclusione, i raggi che incidono sulla goccia ad una distanza prossima (un po' inferiore o un po' maggiore) a 0.86 R, escono dalla medesima approssimativamente con un angolo di ![]() . Come detto, ciò significa che attorno a questo valore si forma una concentrazione di raggi che si traduce in una maggiore intensità luminosa rispetto alla luce diffusa dalla goccia nelle regioni relative ad angoli inferiori: è tale fatto che dà origine all'arcobaleno primario.
. Come detto, ciò significa che attorno a questo valore si forma una concentrazione di raggi che si traduce in una maggiore intensità luminosa rispetto alla luce diffusa dalla goccia nelle regioni relative ad angoli inferiori: è tale fatto che dà origine all'arcobaleno primario.
Le due figure successive aiutano a cogliere con una rappresentazione più realistica la formazione dell'arcobaleno primario: un certo numero di raggi paralleli ed equispaziati (la goccia è quindi illuminata uniformemente) e incidenti sulla parte superiore della goccia escono da essa in diverse direzioni ma addensandosi in prossimità dell'angolo di arcobaleno: nella prima si tracciano 40 raggi incidenti mentre nella seconda i raggi incidenti sono in numero di 100 per evidenziare tale addensamento.
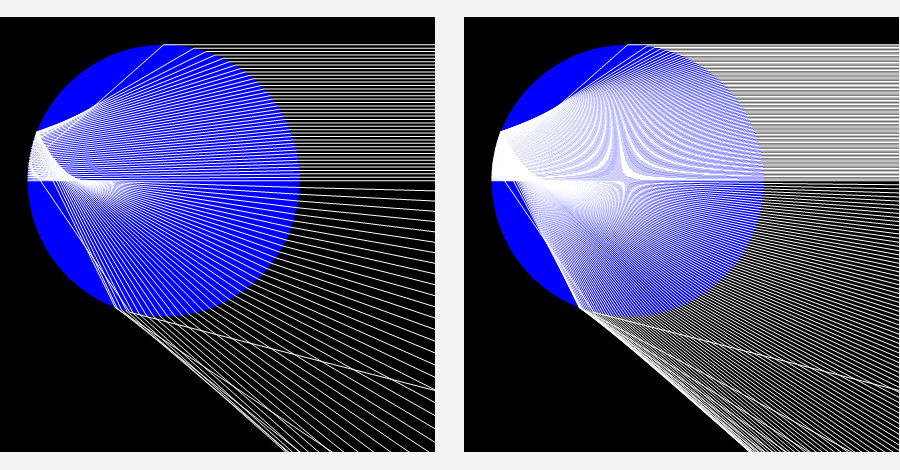
Figura 8. Addensamento dei raggi emergenti attorno all'angolo di arcobaleno: il numero di raggi è di 40 a sinistra, di 100 alla destra.
Nella figura 9 il numero di raggi incidenti è aumentato a 400 ma sono distribuiti su tutta la superficie della goccia d'acqua e sono stati eliminati i raggi incidenti e il loro percorso interno: ciò mette in evidenza non solo l'addensamento attorno al valore critico ma pure come una goccia d'acqua costituisca un significativo centro di diffusione luminosa. Più avanti evidenzieremo la maggiore intensità luminosa in corrispondenza dell'angolo di arcobaleno tramite una simulazione numerica.

Figura 9. Distribuzione di 400 raggi emergenti da una goccia.
Infine una rappresentazione in 3D (figura 10) dove si evidenza il percorso seguito da un certo numero (40) di raggi incidenti aventi lo stesso parametro d'impatto. Variando tale parametro nella corrispondente animazione si possono riprodurre le osservazioni fatte a proposito della figura 2 iniziale.
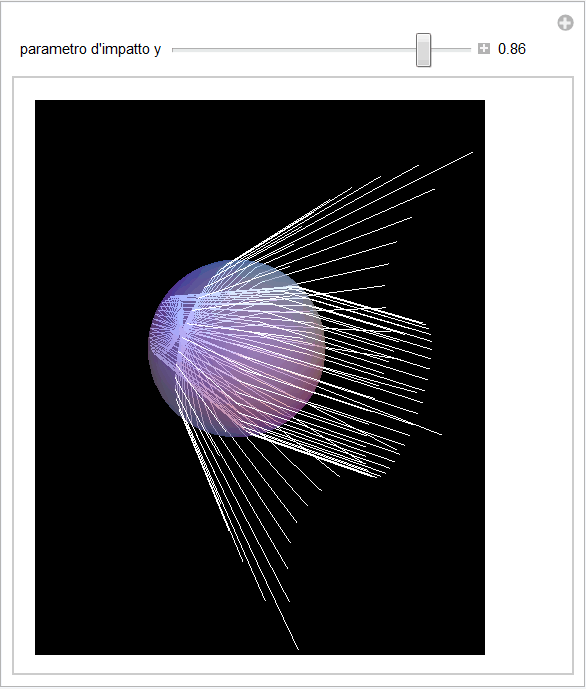
Figura 10. Rappresentazione 3D di 40 raggi incidenti e i corrispondenti raggi emergenti.
Condizioni per osservare l'arcobaleno primario
Nella sezione precedente abbiamo concluso che la massima intensità diffusa verso l'osservatore dalle gocce di pioggia si colloca ad un angolo attorno i 42°. La regione di pioggia che rimanda all'osservatore i raggi di luce con tale angolo dovrà pertanto apparire più luminosa delle regioni vicine che invece diffondono ad angoli diversi e, per quanto detto, evidentemente minori: è questa regione che quindi costituisce l'arcobaleno.
Per poter osservare tale fenomeno i raggi diffusi dalle gocce devono poter convergere verso l'osservatore con tale angolo, che è fisso, e pari appunto a circa ![]() .
.
Se quindi ![]() è l'altezza angolare del sole sull'orizzonte (angolo evidenziato in rosso nella figura 11), sappiamo che i raggi solari incidono parallelamente sia sulla regione investita dalla pioggia (in azzurro) sia sull'osservatore (si veda anche la precedente figura 4). Se, come detto, richiamiamo la definizione di punto antisolare, individuabile praticamente dalla posizione dell'ombra del capo dell'osservatore sul terreno (foto 2), per raggiungere la regione dell'arcobaleno è sufficiente tracciare una linea che formi con questa direzione un angolo pari ad
è l'altezza angolare del sole sull'orizzonte (angolo evidenziato in rosso nella figura 11), sappiamo che i raggi solari incidono parallelamente sia sulla regione investita dalla pioggia (in azzurro) sia sull'osservatore (si veda anche la precedente figura 4). Se, come detto, richiamiamo la definizione di punto antisolare, individuabile praticamente dalla posizione dell'ombra del capo dell'osservatore sul terreno (foto 2), per raggiungere la regione dell'arcobaleno è sufficiente tracciare una linea che formi con questa direzione un angolo pari ad ![]() (in arancio nella figura 11).
(in arancio nella figura 11).

Foto 2. Arcobaleno e punto antisolare (http://it.wikipedia.org/wiki/Arcobaleno).
L'intersezione di tale linea con la regione investita dalla pioggia individua la posizione l'arcobaleno. Difatti dal punto di vista geometrico, tale linea non è altro che una trasversale di un fascio di rette parallele, i raggi solari, che forma con tali rette angoli alterni interni pari a ![]() (figura 11).
(figura 11).

Figura 11. Altezza angolare del sole e osservabilità dell'arcobaleno.
È ora immediato determinare le condizioni per osservare l'arcobaleno in quanto tale regione dev'essere al di sopra dell'orizzonte (linea tratteggiata in figura 11) ossia la sua altezza angolare ![]() (in arancio con bordo verde) dovrà essere maggiore di zero,
(in arancio con bordo verde) dovrà essere maggiore di zero, ![]() . Poiché tra gli angoli discussi sussiste la semplice relazione (e
. Poiché tra gli angoli discussi sussiste la semplice relazione (e ![]() , lo ripetiamo, è costante)
, lo ripetiamo, è costante)
| (17) |
si ricava ![]() cosicché la condizione
cosicché la condizione
| (18) |
implica
| (19) |
È pertanto possibile osservare l'arcobaleno primario se è solo se l'altezza del sole sull'orizzonte è inferiore ai 42°: questo spiega il fatto che in pieno giorno non si osservano arcobaleni mentre questi si rilevano solo nelle prime ore del mattino o verso sera, in particolare fino a circa tre ore dopo l'alba o approssimativamente entro le tre ore prima del tramonto (si tenga presente che la velocità angolare terrestre è di 15° all'ora).
In base alla relazione (18), l'altezza dell'arcobaleno sarà massima quando ![]() ossia quando il sole si trova all'orizzonte: in tal caso l'altezza è pari a
ossia quando il sole si trova all'orizzonte: in tal caso l'altezza è pari a ![]() . Comunque, per ogni valore dell'altezza del sole compresa
. Comunque, per ogni valore dell'altezza del sole compresa ![]() l'osservatore si può pensare nel vertice di un cono di apertura fissa
l'osservatore si può pensare nel vertice di un cono di apertura fissa ![]() e con asse coincidente con il raggio solare passante per l'osservatore e il punto antisolare (figura 13). Quest'ultima osservazione permette di interpretare geometricamente l'arcobaleno come quella linea che si ottiene dalla sezione di tale cono con il piano verticale contenente le gocce di pioggia. Quindi, se poniamo l'ipotesi restrittiva che tale strato abbia uno spessore trascurabile rispetto alla distanza dall'osservatore potremo aggiungere queste ulteriori considerazioni di carattere geometrico: il tipico arco dell'arcobaleno potrà essere un semicirconferenza solo nel caso in cui l'altezza solare sia nulla: in tal caso l'asse del cono e il piano delle gocce sono perpendicolari. In tutti gli altri casi, non potrà che essere un arco di ellisse dato che questa è la sezione che si ottiene tra piano e cono quando l'asse di quest'ultimo formi con il piano stesso angoli maggiori della sua apertura e minori di 90°.
e con asse coincidente con il raggio solare passante per l'osservatore e il punto antisolare (figura 13). Quest'ultima osservazione permette di interpretare geometricamente l'arcobaleno come quella linea che si ottiene dalla sezione di tale cono con il piano verticale contenente le gocce di pioggia. Quindi, se poniamo l'ipotesi restrittiva che tale strato abbia uno spessore trascurabile rispetto alla distanza dall'osservatore potremo aggiungere queste ulteriori considerazioni di carattere geometrico: il tipico arco dell'arcobaleno potrà essere un semicirconferenza solo nel caso in cui l'altezza solare sia nulla: in tal caso l'asse del cono e il piano delle gocce sono perpendicolari. In tutti gli altri casi, non potrà che essere un arco di ellisse dato che questa è la sezione che si ottiene tra piano e cono quando l'asse di quest'ultimo formi con il piano stesso angoli maggiori della sua apertura e minori di 90°.
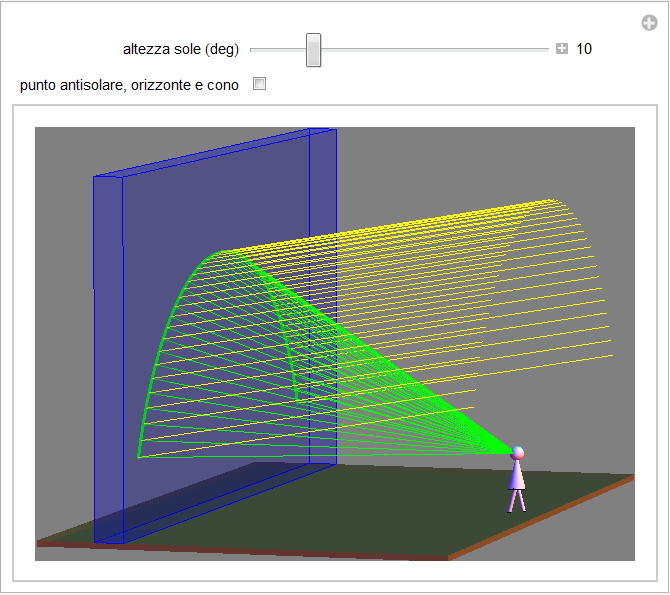
Figura 12. Raggi solari e arcobaleno visto dall'osservatore.
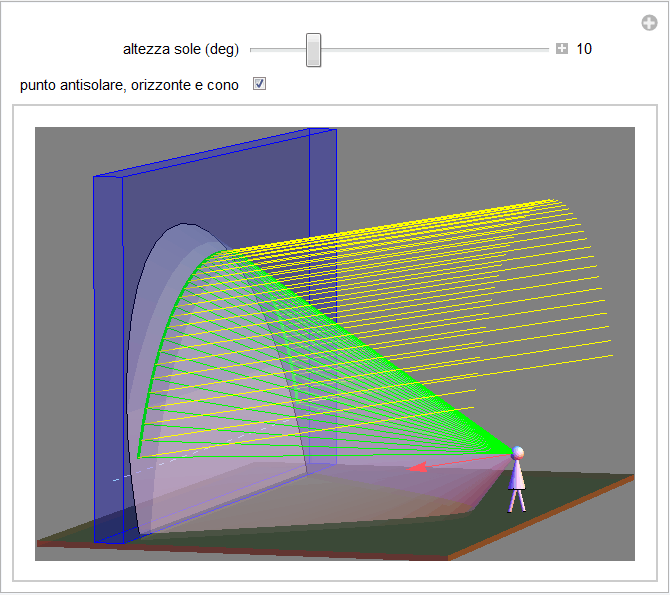
Figura 13. Raggi di arcobaleno, cono dell'osservatore e direzione antisolare.
I colori del primario
La dispersione
Per ottenere la spiegazione di una caratteristica fondamentale dell'arcobaleno e cioè dei suoi colori e della loro successione va considerato che quanto esposto nelle sezioni precedenti vale per un raggio monocromatico cioè di una particolare lunghezza d'onda (nel nostro caso quella del colore verde). In effetti abbiamo sempre considerato un indice di rifrazione pari a n = 4/3 mentre questa grandezza dipende, seppur leggermente, con la lunghezza d'onda della luce incidente. Il legame tra indice di rifrazione n e lunghezza d'onda λ non possiede una rappresentazione analitica semplice per cui anziché fornirne una analitica approssimata preferiamo interpolare i dati sperimentali riportati nella tavola 1 seguente (si veda quale riferimento [1]): questa associa alla lunghezza d'onda λ, espressa in multipli di ![]() m, il corrispondente indice di rifrazione e il colore associato.
m, il corrispondente indice di rifrazione e il colore associato.
| lunghezza d'onda (nm) |
indice di rifrazione | colore |
| 400 | 1.34451 |  |
| 425 | 1.34235 |  |
| 450 | 1.34055 |  |
| 475 | 1.33903 |  |
| 500 | 1.33772 |  |
| 525 | 1.33659 |  |
| 550 | 1.3356 |  |
| 575 | 1.33472 |  |
| 600 | 1.33393 |  |
| 625 | 1.33322 |  |
| 650 | 1.33257 |  |
| 675 | 1.33197 |  |
| 700 | 1.33141 |  |
Tavola 1. Lunghezza d'onda, indice di rifrazione e colore.
Come si può cogliere facilmente, all'aumentare della lunghezza d'onda e quindi passando dal violetto verso il rosso, l'indice di rifrazione diminuisce leggermente ma costantemente. Indicata simbolicamente la funzione che interpola i dati della tavola 1 con n(λ), forniamo il suo grafico (figura 14) assieme ai dati stessi e, come sfondo, il colore corrispondente.
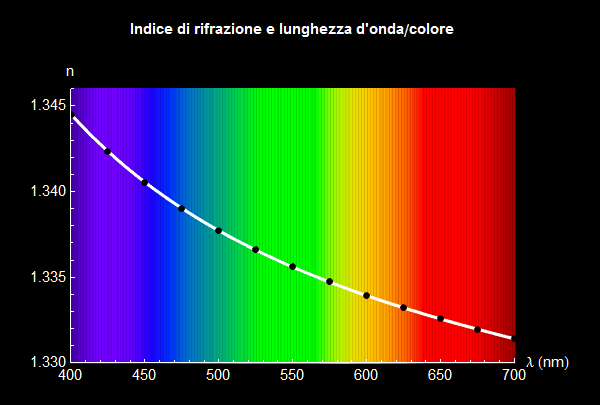
Figura 14. Dipendenza dell'indice di rifrazione dalla lunghezza d'onda.
L'andamento mostra chiaramente la diminuzione dell'indice di rifrazione dell'acqua con la lunghezza d'onda cosicché, riferendoci agli estremi dello spettro, se ![]() è l'indice di rifrazione del violetto e
è l'indice di rifrazione del violetto e ![]() quello del rosso, dalla disuguaglianza
quello del rosso, dalla disuguaglianza ![]() e dalla legge della rifrazione scritta come
e dalla legge della rifrazione scritta come
| (20) |
deduciamo che, a parità di angolo di incidenza, sin(r) è inversamente proporzionale all'indice n cosicché
| (21) |
ossia
| (22) |
Poichè la deviazione subita in una rifrazione è data dalla differenza δ = i - r e l'angolo di incidenza i è il medesimo, segue che il rosso è deviato di meno del violetto ossia ![]() . Ciascuna componente monocromatica compresa tra questi estremi avrà un suo angolo di rifrazione e il raggio incidente risulterà disperso in acqua in un intervallo angolare di estremi
. Ciascuna componente monocromatica compresa tra questi estremi avrà un suo angolo di rifrazione e il raggio incidente risulterà disperso in acqua in un intervallo angolare di estremi ![]() : è questo il fenomeno della dispersione.
: è questo il fenomeno della dispersione.
La figura 15 rappresenta, esagerandolo, tale fenomeno (l'animazione associata nel notebook permette di simulare la dispersione cromatica e, variando opportunamente un parametro, è possibile renderlo più evidente amplificando l'angolo dell'estremo violetto. Se poi si aumenta il numero di raggi si può cogliere la distribuzione degli altri colori dello spettro compresi tra quelli estremi).
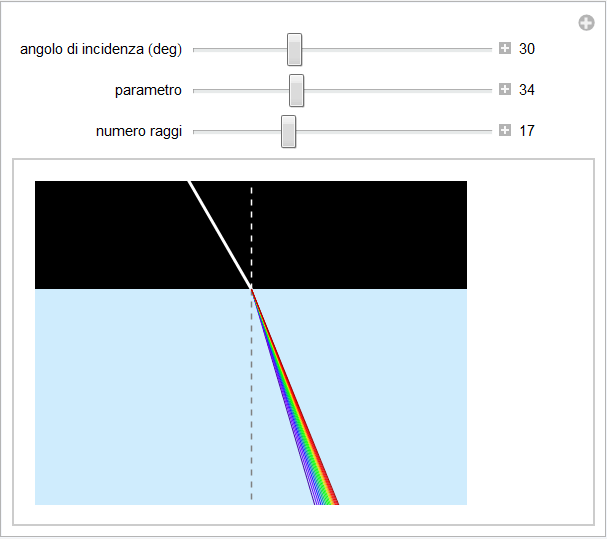
Figura 15. Dispersione di un raggio di luce bianca nelle componenti monocromatiche dello spettro.
I colori
A seguito della dispersione, ciascuna componente monocromatica della luce solare seguirà un suo percorso entro la goccia e ne uscirà con angoli di emergenza e quindi con angoli di arcobaleno diversi. La figura 16 mostra, in forme amplificate, l'effetto della dispersione da parte della goccia (l'animazione nel notebook permette di analizzare quanto avviene nelle due rifrazioni e quindi la dispersione angolare delle singole componenti monocromatiche. Riportando lo zoom a valori tra 4 e 5 appaiono visivamente gli angoli di arcobaleno dei colori estremi o del numero impostato di raggi e si può notare come l'angolo di arcobaleno del rosso sia sempre maggiore di quello del violetto).
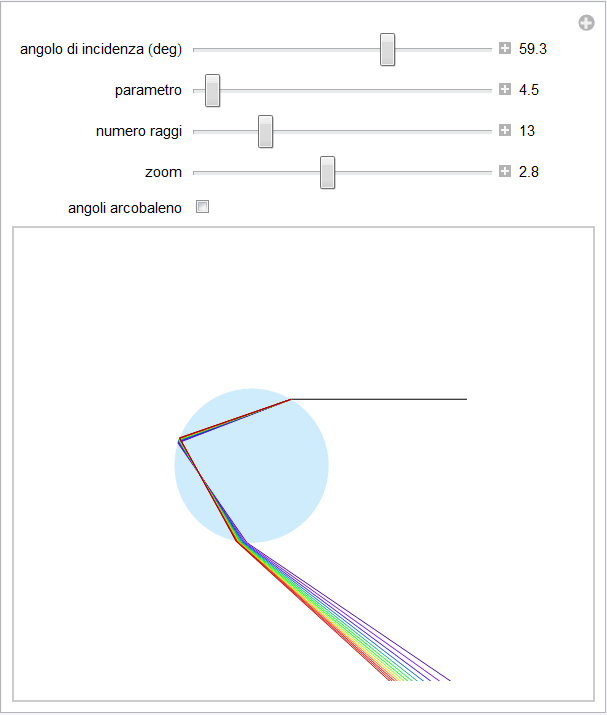
Figura 16. Dispersione da parte di una goccia di un raggio non monocromatico nelle sue componenti spettrali.
Poiché, per quanto visto precedentemente, l'intensità massima si ottiene in corrispondenza dell'angolo di arcobaleno ![]() , ad ogni lunghezza d'onda possiamo associare l'angolo, misurato rispetto al punto antisolare, in corrispondenza del quale si osserva l'arcobaleno di quel particolare colore. La funzione che fornisce tale angolo si ottiene dalla (15) sostituendo all'indice di rifrazione n là presente, la funzione n(λ) e cioè
, ad ogni lunghezza d'onda possiamo associare l'angolo, misurato rispetto al punto antisolare, in corrispondenza del quale si osserva l'arcobaleno di quel particolare colore. La funzione che fornisce tale angolo si ottiene dalla (15) sostituendo all'indice di rifrazione n là presente, la funzione n(λ) e cioè
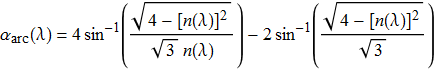 |
(23) |
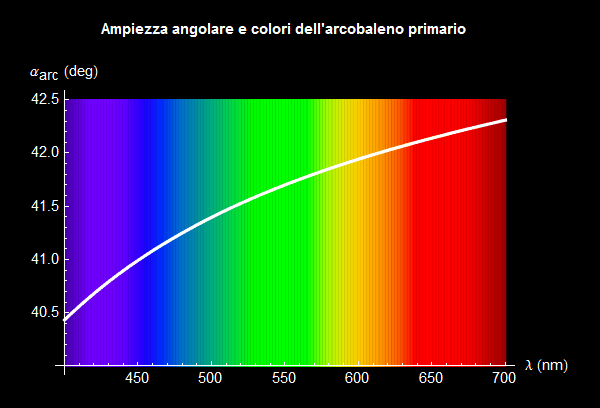
Figura 17. Angoli di arcobaleno e lunghezza d'onda/colore.
Come si vede (fig. 17), il violetto forma una arcobaleno attorno ai 40.5° mentre la componente rossa lo forma attorno ai 42°. In particolare, con i dati della tavola 1, l'arcobaleno primario si forma entro un angolo compreso tra gli estremi [40.43°, 42.31°] (tavola 2). L'ampiezza angolare di un arcobaleno primario è quindi poco meno di 2°.
| ampiezza αarc (deg) |
colori estremi dello spettro |
| 40.43 |  |
| 42.31 |  |
Tavola 2. Angoli di arcobaleno per i colori estremi dello spettro.
Nella figura 18 riportiamo la struttura dell'arcobaleno primario dilatata radialmente di circa 8 volte allo scopo di cogliere la successione dei colori mentre nella figura 19 si riprende una sua rappresentazione tridimensionale.
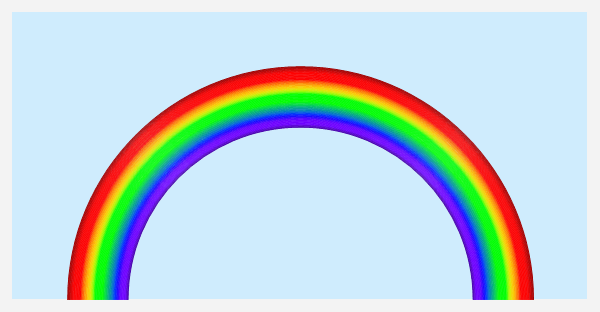
Figura 18. Struttura dell'arcobaleno primario con il sole all'orizzonte e dilatata radialmente di un fattore 8.
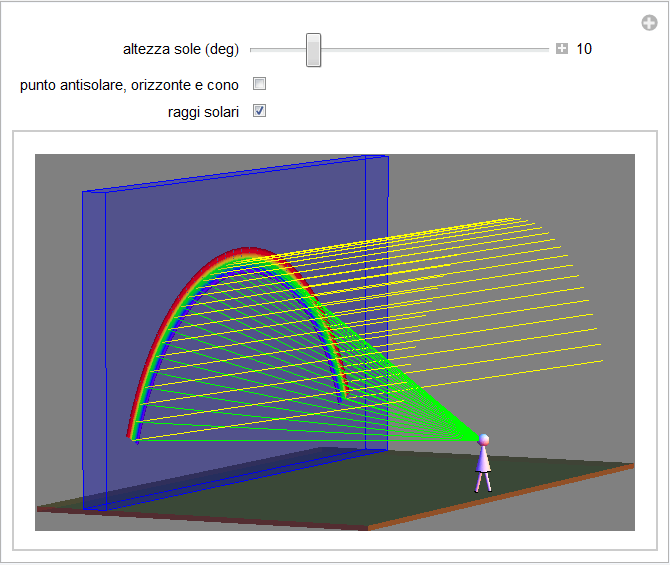
Figura 19. Raggi solari, arcobaleno primario e colori.

Foto 3. Arcobaleno primario particolarmente luminoso (luogo: Magrè di Schio, Vicenza).

Foto 4. Arcobaleno primario.
Arcobaleno secondario

Foto 5. Arcobaleno primario e secondario (www.fotovallescrivia.it)
Percorso dei raggi solari e angolo di arcobaleno secondario
In particolari situazioni collegate all'altezza del sole, alle dimensioni della zona investita dalla pioggia, alla posizione dell'osservatore, si può osservare in aggiunta al comune arcobaleno pure un secondo arcobaleno, generalmente meno luminoso e disposto al di sopra dell'arcobaleno propriamente detto o arcobaleno primario: è questo il cosiddetto arcobaleno secondario (foto 5, ma pure nelle precedenti.).
L'arcobaleno secondario si spiega ancora tramite la rifrazione considerando il percorso di un raggio che incide su una goccia d'acqua sferica ma che, a differenza dell'arcobaleno primario, subisce invece due riflessioni al suo interno (figura 20).
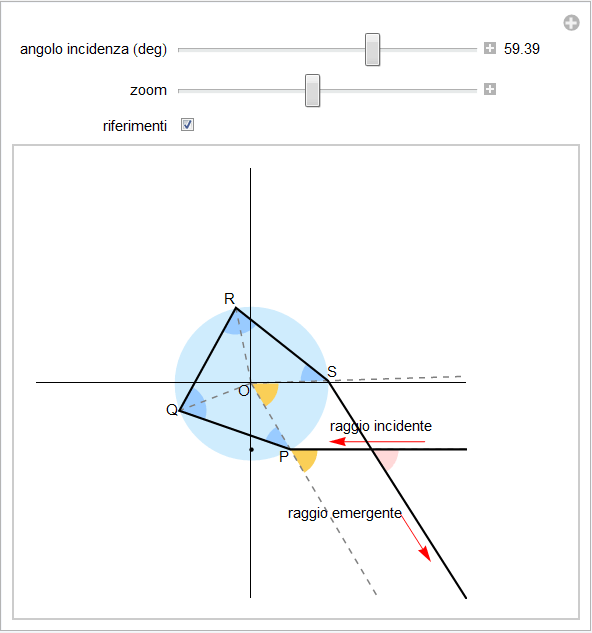
Figura 20. Percorso di un raggio di luce dell'arcobaleno secondario.
L'angolo δ che dà la deviazione totale rispetto alla direzione originaria si ottiene ancora come somma delle singole deviazioni subite dal raggio luminoso. Come già visto,
nella prima rifrazione: questa è pari a i - r (punto P)
nella prima riflessione interna: π - 2r (punto Q)
nella seconda riflessione interna: π - 2r (punto R)
nella seconda rifrazione è ancora i - r (punto S)
per cui in totale risulta
| (24) |
Ovviamente la situazione interessante si presenta quando il raggio viene deviato nella direzione dell'osservatore (disposto nelle nostre figure sempre in basso a destra rispetto alla goccia). Pertanto l'angolo di diffusione secondario, angolo che indicheremo con β (in colore rosa nella figura 20), è il supplementare della deviazione totale δ cosicché si ha
| (25) |
La dipendenza di β dall'angolo di incidenza i si ottiene riprendendo la legge della rifrazione (3) e sostituendola in luogo di r
| (26) |
In corrispondenza del valore standard (n = 4/3) utilizzato finora per l'indice di rifrazione, tale funzione possiede il grafico di figura 21.
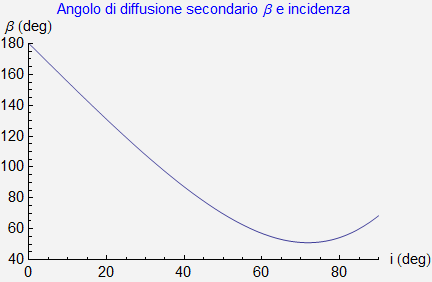
Figura 21. Angolo di diffusione secondario e angolo d'incidenza.
In questo caso l'angolo β presenta un minimo anziché un massimo ma, in analogia a quanto fatto per l'arcobaleno primario, esprimiamo tale angolo in termini del parametro di impatto y = R sin(i)
| (27) |
e quindi riportiamo il grafico di β(y) assieme alla corrispondente rappresentazione geometrica del percorso (fig. 22).
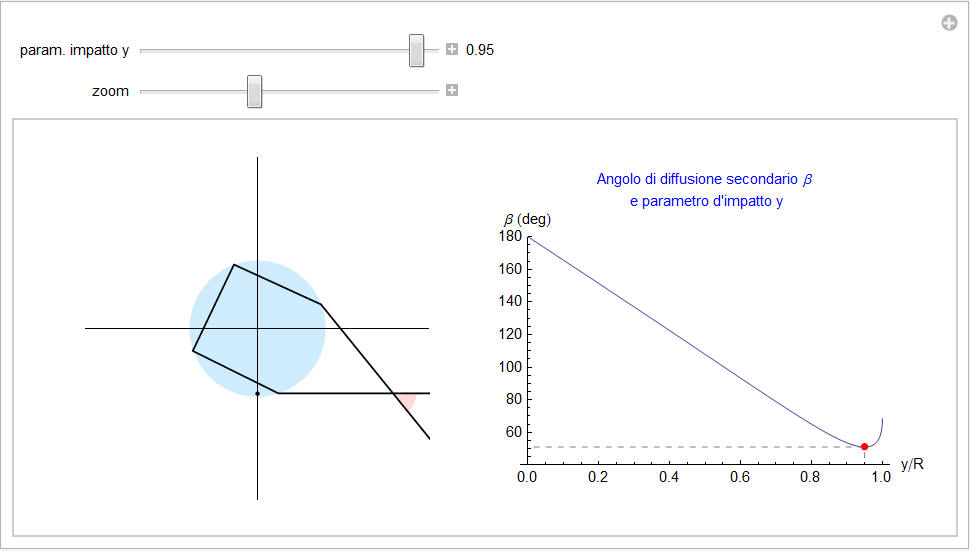
Figura 22. Angolo di diffusione secondario e rappresentazione geometrica del percorso.
Possiamo ora riproporre le medesime considerazioni esposte per l'arcobaleno primario: anche in questo caso la goccia disperde i raggi luminosi in un ampio intervallo angolare, a partire comunque da un valore minimo approssimativamente attorno ai 50°. Rappresentando l'intensità uniforme incidente sulla goccia tramite un certo numero di raggi egualmente distribuiti nell'intervallo [0, R], la figura 23 ripropone l'addensamento dei raggi diffusi attorno al minimo nello stesso modo in cui la figura 7 lo fa per il primario.
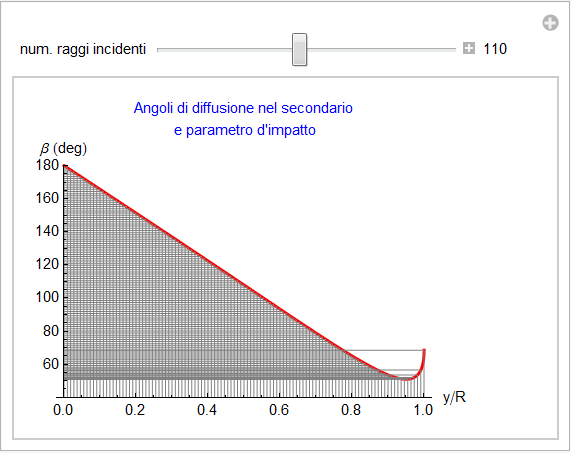
Figura 23. Angolo di diffusione secondario e addensamento dei raggi diffusi in prossimità del minimo.
Passando invece ad una rappresentazione più realistica della diffusione dei raggi riflessi internamente due volte, la figura 24a mostra inizialmente il percorso seguito da 100 raggi incidenti e quindi diffusi dalla goccia mentre nella seconda immagine si è scelto di rappresentare solo le direzioni di diffusione di 250 raggi emergenti. In quest'ultima immagine appare più evidente la maggiore densità dei raggi in prossimità del minimo.
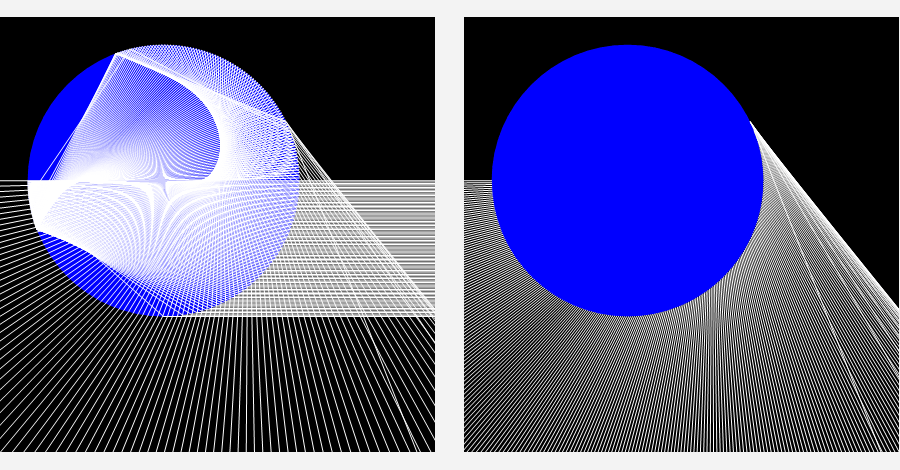
Figura 24. Direzioni di diffusione da parte di una goccia per raggi riflessi internamente due volte.
Il valore del parametro d'impatto cui corrisponde il minimo, ![]() , si trova sempre con i metodi dell'Analisi Matematica e risulta
, si trova sempre con i metodi dell'Analisi Matematica e risulta
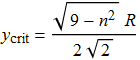 |
(28) |
che, con i valori standard finora utilizzati fornisce per y il valore
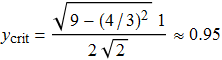 |
(29) |
Pertanto i raggi che incidono con questo parametro o in prossimità di esso e che, a ben vedere, sono molto prossimi al raggio che incide tangenzialmente alla goccia, sono i responsabili dell'arcobaleno secondario.
Il valore dell'angolo di arcobaleno secondario ![]() in corrispondenza del quale si ha la massima intensità luminosa dell'arcobaleno secondario (e il minimo dell'angolo di diffusione) si ottiene sostituendo la (28) nella (27)
in corrispondenza del quale si ha la massima intensità luminosa dell'arcobaleno secondario (e il minimo dell'angolo di diffusione) si ottiene sostituendo la (28) nella (27)
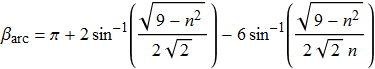 |
(30) |
ancora indipendente dal raggio della goccia. Con i valori standard finora utilizzati tale angolo risulta
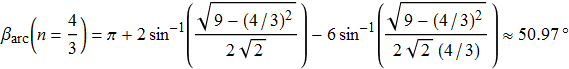 |
(31) |
e di conseguenza l'arcobaleno secondario si colloca mediamente attorno ai 51° rispetto al punto antisolare.
Banda oscura di Alessandro
Nelle sezioni precedenti abbiamo dedotto le espressioni degli angoli di diffusione primario (12)
| (32) |
e secondario (27)
| (33) |
in termini del parametro d'impatto. Disponendo ora i relativi grafici sullo stesso piano cartesiano si ottiene la rappresentazione di figura 25.
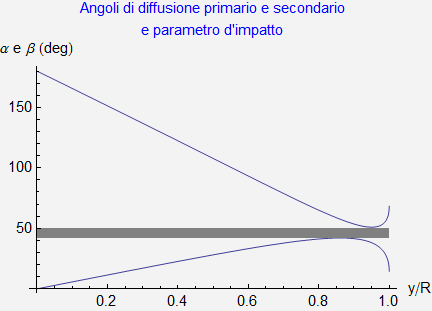
Figura 25. Angoli di diffusione primario e secondario.
Questa mette in evidenza un fatto interessante: nell'intervallo angolare di estremi [42°, 51°] evidenziato in grigio nella figura (e relativo a n = 4/3), le gocce di pioggia non diffondono verso l'osservatore alcun raggio luminoso tra quelli finora considerati e cioè tra quelli che subiscono una o due riflessioni interne. E poiché tale grafico descrive come una goccia diffonde una significativa frazione della luce solare ne segue che la zona di cielo corrispondente a tale intervallo angolare apparirà all'osservatore meno luminosa delle adiacenti (che, all'opposto, appariranno più chiare). In effetti questa è un'altra caratteristica dell'arcobaleno, comunemente non rilevata da un osservatore occasionale ma che all'osservatore attento non può sfuggire: tra l'arco del primario e del secondario il cielo appare più scuro delle zone interne ed esterne ai due archi (vedi foto 1, 2, 3, 5, 6, 7): tale zona viene detta banda oscura di Alessandro dal nome del filosofo Alessandro di Afrodisia che per primo la descrisse.

Foto 6. Arcobaleno primario, secondario e banda di Alessandro.

Foto 7. Arcobaleno primario, secondario e banda di Alessandro.
I colori del secondario
Per comprendere la successione dei colori nell'arcobaleno secondario va considerato il fenomeno della dispersione e quindi la variazione dell'indice di rifrazione con la lunghezza d'onda. La legge n(λ) che lega queste due grandezze è riassunta nel grafico di figura 14. A seguito di ciò e a causa dell'ulteriore riflessione subita dai raggi dell'arcobaleno secondario, la dispersione angolare delle diverse componenti monocromatiche deve essere maggiore rispetto all'analoga dispersione nel primario. L'immagine di figura 26 mostra, in forme amplificate, i percorsi delle diverse componenti cromatiche ma, soprattutto, suggerisce come gli angoli di arcobaleno degli estremi dello spettro siano, rispetto al primario, invertiti: tenendo conto che il raggio incidente è orizzontale appare evidente come l'angolo di arcobaleno del violetto sia maggiore di quello del rosso.
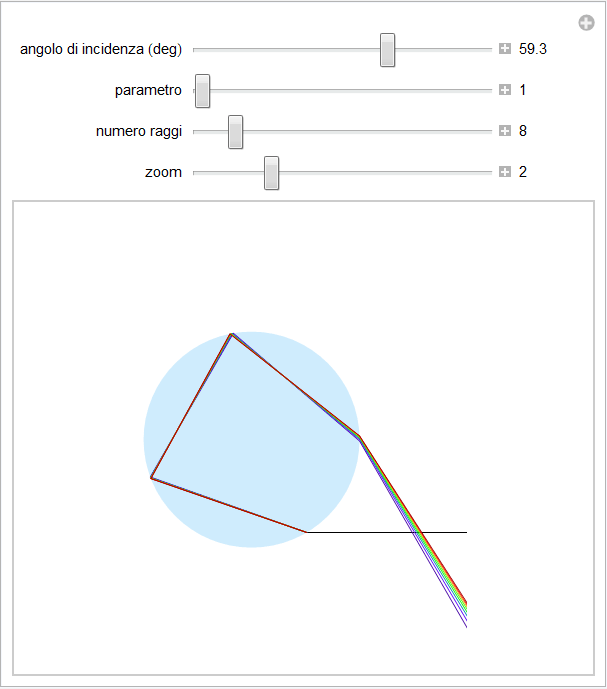
Figura 26. Dispersione angolare di un raggio di luce bianca del secondario e angoli di arcobaleno.
Ciò evidentemente comporta un arco secondario con i colori dello spettro invertiti rispetto all'ordine del primario. Difatti sostituendo nell'angolo di arcobaleno ![]() dato dalla (30) la funzione n(λ) (della quale, come detto, non forniamo la rappresentazione analitica in quanto utilizziamo una sua interpolazione a partire dai dati della tavola 1) ,
dato dalla (30) la funzione n(λ) (della quale, come detto, non forniamo la rappresentazione analitica in quanto utilizziamo una sua interpolazione a partire dai dati della tavola 1) ,
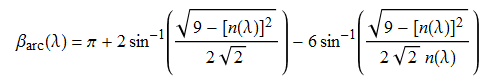 |
(34) |
si ottengono le ampiezze angolari del secondario corrispondenti all'intensità massima di un dato colore o lunghezza d'onda. La figura 27 esplicita l'andamento della (34) al variare di λ nell'intervallo delle lunghezze d'onda del visibile.
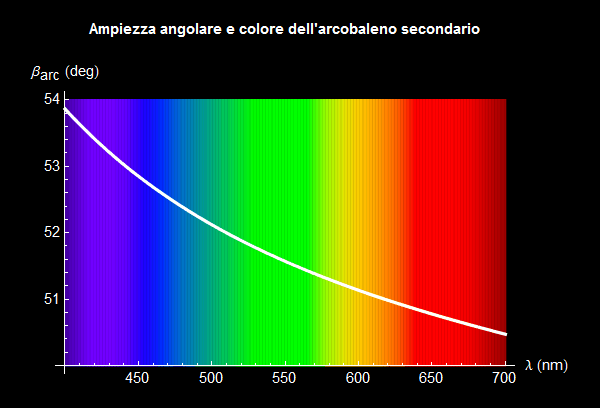
Figura 27. Ampiezze angolari dei diversi colori dello spettro nell'arcobaleno secondario.
In base a tale andamento si può dedurre come, da un'ampiezza di circa 54° per il violetto, si giunga ad una ampiezza di circa 50.5° per il rosso: come prospettato precedentemente l'arcobaleno secondario avrà pertanto il colore rosso nella regione inferiore dell'arco mentre il violetto apparirà nella zona più elevata (tavola 3 e foto 2, 3, 5, 7).
| ampiezza βarc (deg) |
colori estremi dello spettro |
| 50.47 |  |
| 53.86 |  |
Tavola 3. Angolo di arcobaleno secondario per i colori estremi dello spettro.
In particolare la successione che emerge a partire dai valori angolari minori è, in definitiva:
primario: violetto a partire dai 40.3° per finire con il rosso a 42.3°,
banda di Alessandro, dai 42.5° ai 50.5°
secondario: rosso attorno ai 50.5° e quindi violetto a circa 54°.
e, visivamente, è riassunta dalla figura 28 ottenuta unendo i grafici delle figure 17 e 27.
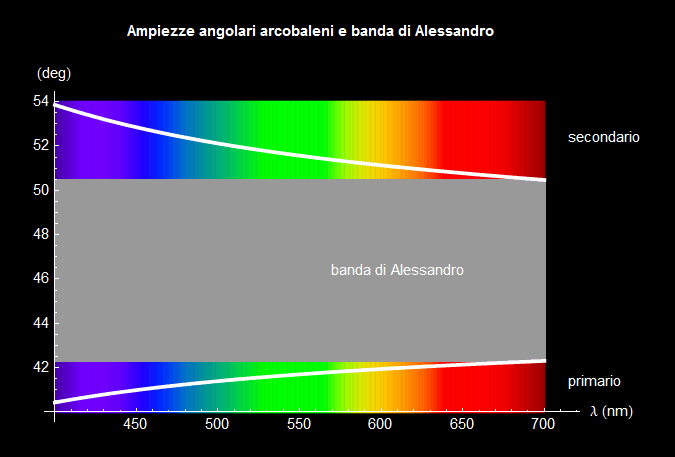
Figura 28. Successione angolare dei colori nell'arcobaleno primario e secondario e banda di Alessandro.
Osservabilità
Concludiamo questa nostra analisi riprendendo, alla luce dell'esistenza dell'arcobaleno secondario, le condizioni di osservabilità dell'arcobaleno. Se per l'osservazione di un arcobaleno primario è necessario che il sole sia ad un'altezza sull'orizzonte inferiore ai 42°, la maggior ampiezza angolare dell'arcobaleno secondario permette di osservarlo anche ad altezze solari maggiori: in particolare poiché il violetto si forma a circa 54° dal punto antisolare, sarà questa l'altezza massima sull'orizzonte: in ogni caso, per altezze solari comprese tra i 42° e i 54° si potrà osservare solo l'arcobaleno secondario che sarà riconoscibile per l'ordine dei colori.
Le figure che seguono riportano visivamente le principali strutture dell'arcobaleno discusse e la loro disposizione spaziale.
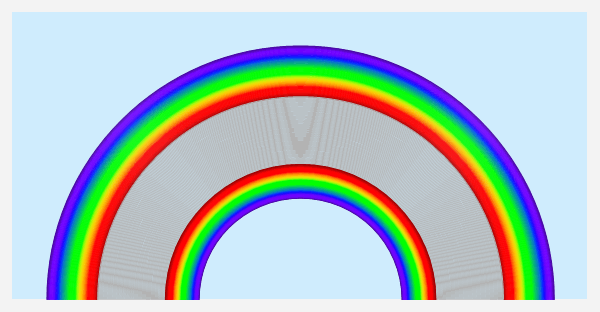
Figura 29. Principali strutture dell'arcobaleno.
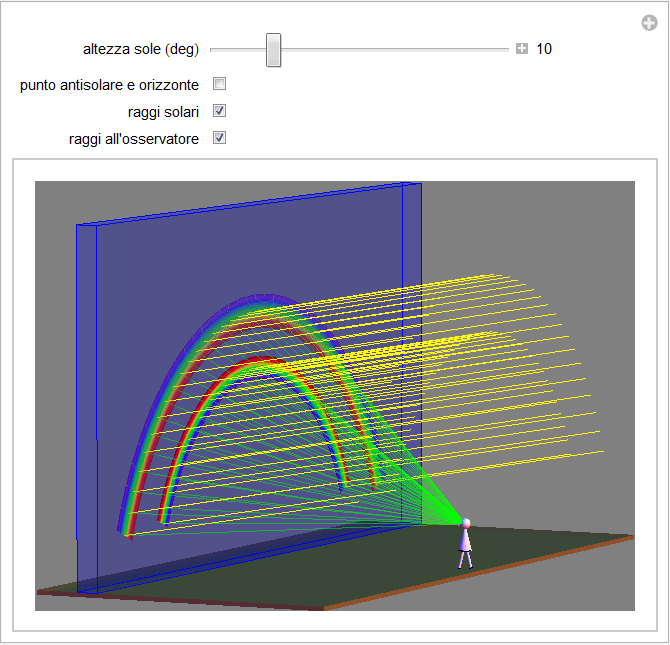
Figura 30. Vista 3D dell'arcobaleno primario e secondario con raggi solari e raggi convergenti all'osservatore.
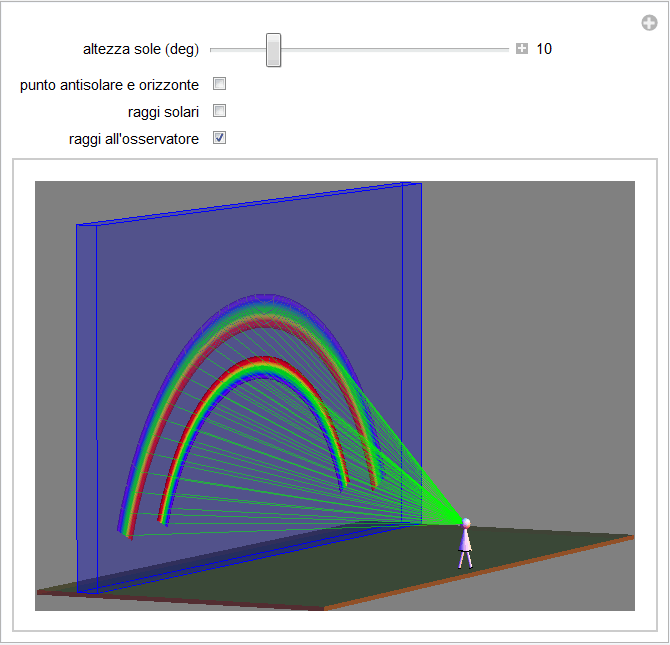
Figura 31. Vista 3D dell'arcobaleno primario e secondario con solo i raggi convergenti all'osservatore.
Aspetti particolari
Coppie di raggi emergenti paralleli
In base al grafico di figura 32 che riprende quello di fig. 7 possiamo notare che per ogni angolo di diffusione α maggiore del minimo raggiunto dalla funzione α(y) nell’estremo destro quando y/R = 1, vi sono due parametri d’impatto distinti e quindi due raggi incidenti: uno avente parametro d’impatto minore e l’altro maggiore del valore critico ![]() (
(![]() con i valori standard) e in corrispondenza del quale viene definito l’angolo di arcobaleno.
con i valori standard) e in corrispondenza del quale viene definito l’angolo di arcobaleno.
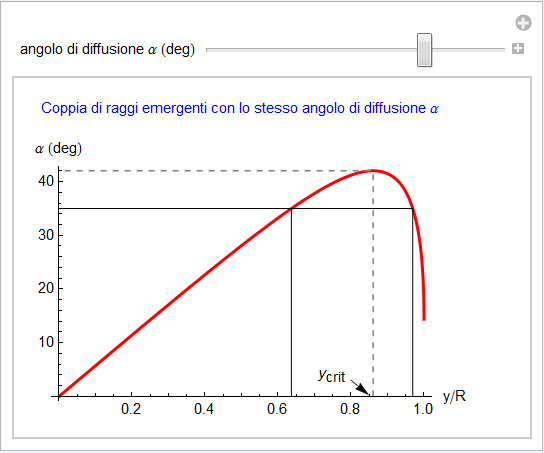
Figura 32. Coppia di raggi incidenti sulla goccia aventi il medesimo angolo di diffusione.
I corrispondenti raggi emergono quindi paralleli (figura 33) pur seguendo ciascuno un percorso diverso entro la goccia. A seconda della differenza tra questi percorsi la fase dei due raggi dovrà cambiare per cui questi potranno interferire costruttivamente o distruttivamente e generare delle frange di interferenza. In effetti l’insieme di queste coppie di raggi dà ragione di un’ulteriore caratteristica dell'arcobaleno, gli archi soprannumerari. Questi appaiono come tenui archi nei quali, quando visibili, si possono cogliere solo alcuni colori dello spettro: ciascun arco presenta quindi un’alternanza tra un pallido colore violetto o blu e un altrettanto pallido color verde. Si osservano al di sotto dell’arcobaleno primario principalmente nella parte superiore piuttosto che alla sua base e la loro visibilità dipende fortemente dalle dimensioni delle gocce di pioggia: piccole gocce con dimensioni attorno a 0.1 mm comportano una separazione maggiore tra un arco soprannumerario e il successivo e ne facilitano l’osservabilità mentre se le gocce sono maggiori (attorno a 0.5 mm) tali archi non saranno nemmeno visibili. In ogni caso la loro spiegazione esce dall’ambito dell’ottica geometrica per entrare in quello dell’ottica fisica dove intervengono fenomeni quali l’interferenza e la diffrazione e principi quali quello di sovrapposizione.
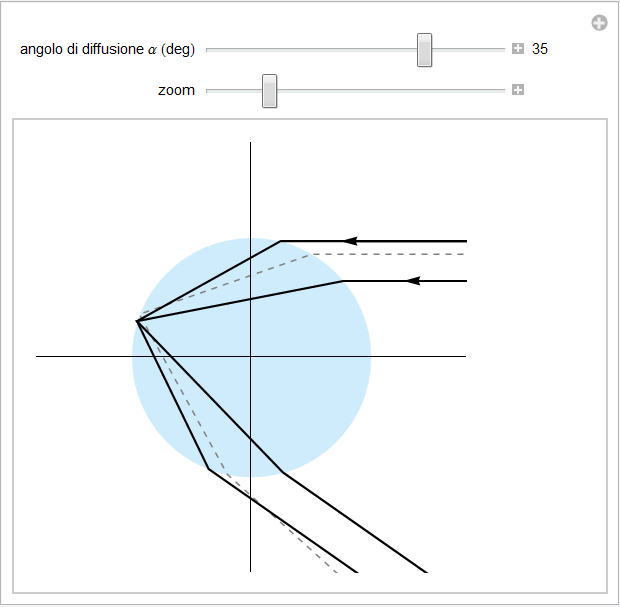
Figura 33. Raggi emergenti con il medesimo angolo di diffusione e quindi paralleli.

Foto 8. Archi soprannumerari (da Wikipedia, www.andrewdunnphoto.com).
Gli archi soprannumerari appaiono pure nelle foto 2 e 11. La successiva è invece un ingrandimento della 2.

Foto 9. Particolare della foto 2 che evidenzia gli archi soprannumerari.
Distribuzione in intensità dei colori
Per avere un'idea più precisa circa l'intensità luminosa proveniente da una goccia d'acqua studiamo più accuratamente la distribuzione angolare dei raggi emergenti dalla goccia dopo una riflessione interna. Intendiamo quindi sostanzialmente calcolare la densità dei raggi che emergono dalla goccia al variare dell'angolo di diffusione: tale funzione non esprime l’intensità luminosa ma la simula e dà quindi un’idea di essa. Come suggerisce graficamente la figura 8 dove appare un addensamento di raggi in prossimità dell'angolo di diffusione massimo, ci aspettiamo pure sulla base di una indagine numerica che tale numero sia maggiore in prossimità, appunto, dell'angolo di arcobaleno.
A tale scopo eseguiremo le seguenti operazioni:
faremo incidere sulla goccia un elevato numero di raggi, tutti paralleli ed equidistanti uno dall'altro così da simulare l'intensità uniforme della luce proveniente dal sole.
Poiché ci è noto l'angolo di arcobaleno primario ![]() oltre il quale non vi sono raggi emergenti dopo una riflessione interna (per cui l'intensità è certamente nulla), fissiamo con una certa arbitrarietà un angolo di diffusione minimo
oltre il quale non vi sono raggi emergenti dopo una riflessione interna (per cui l'intensità è certamente nulla), fissiamo con una certa arbitrarietà un angolo di diffusione minimo ![]() (tale valore può essere lo zero ma per comodità lo sceglieremo attorno ai trenta gradi).
(tale valore può essere lo zero ma per comodità lo sceglieremo attorno ai trenta gradi).
Diviso l'intervallo ![]() in un certo numero n di intervalli più piccoli (nel calcolo proposto sotto è n = 250),
in un certo numero n di intervalli più piccoli (nel calcolo proposto sotto è n = 250),
andremo quindi a contare quanti raggi emergenti sono compresi in ciascuno di questi piccoli intervalli angolari.
Eseguiamo poi il rapporto tra il numero I dei raggi in tal modo ottenuto e il corrispondente valore massimo ![]() , così da disporre di un valore relativo
, così da disporre di un valore relativo ![]() tale che sia
tale che sia ![]() . Questo valore rappresenterà per noi l'intensità, relativamente al massimo, della luce diffusa dalla goccia.
. Questo valore rappresenterà per noi l'intensità, relativamente al massimo, della luce diffusa dalla goccia.
Infine disporremo in un grafico le coppie di punti aventi per ascissa il punto medio dell'intervallo angolare e in ordinata la corrispondente intensità relativa ![]() .
.
Come si vede dalla figura 34 la distribuzione che si ottiene conferma l’addensarsi dei raggi in prossimità dell’angolo di arcobaleno in quanto l’intensità presenta un evidente e pronunciato massimo in corrispondenza di tale angolo. Diminuisce quindi rapidamente al diminuire dell’angolo di diffusione.
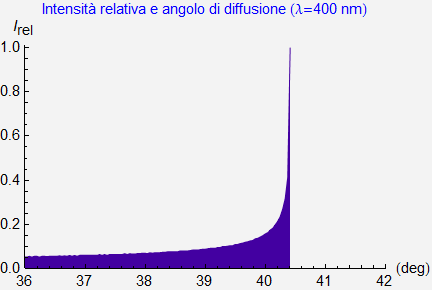
Figura 34. Distribuzione dell’Intensità relativa al variare dell’angolo di diffusione.
La successiva animazione permette di variare la lunghezza d’onda e osservare lo spostamento del massimo di intensità nel campo del visibile quindi a partire da λ = 400 nm e fino ai 700 nm. La struttura dell’andamento complessivo rimane inalterata mentre si può cogliere l’aumento dell’angolo di arcobaleno all’aumentare di λ come rappresentato in altro modo dalla figura 17.
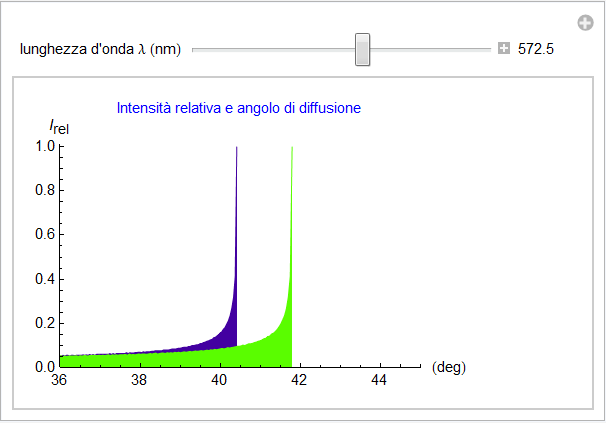
Figura 35. Intensità relativa e lunghezza d’onda/colore.
Infine nella immagine successiva sono rappresentate le intensità relative e il corrispondente colore distanziate una dall’altra di 30 nm e a partire da λ = 400 nm. Riemerge ancora la separazione angolare dei massimi di intensità corrispondenti ai vari colori nell’intervallo già discusso [40.43°, 42.31°] e che vanno a formare l’arcobaleno primario.
D’altra parte la luce emerge dalle gocce di pioggia pure ad angoli di diffusione minori ossia converge all’osservatore con angoli minori di ![]() rispetto al punto antisolare: questi raggi dovranno pertanto provenire dalla gocce localizzate entro l’arco dell’arcobaleno primario. Comunque, in base al grafico di figura 36 a partire da un angolo prossimo ai 40° e muovendoci verso valori inferiori non vi sono più massimi di intensità per cui la luce proveniente da tale regione non mostrerà alcuna prevalenza di qualche colore sugli altri. Ciò spiega un’ultima caratteristica associata all’arcobaleno ossia la maggiore luminosità del cielo nelle zone sottostanti l’arco del primario: in effetti questa luminosità biancastra è generata dalla sovrapposizione dei raggi diffusi ad angoli minori dell’angolo di arcobaleno del violetto e, a tale luminosità, contribuiscono in modo sostanzialmente uniforme tutte le lunghezze d’onda del visibile. Le foto 3, 5, 6, 7 e 10 manifestano tutte questa maggiore luminosità del cielo entro il primario.
rispetto al punto antisolare: questi raggi dovranno pertanto provenire dalla gocce localizzate entro l’arco dell’arcobaleno primario. Comunque, in base al grafico di figura 36 a partire da un angolo prossimo ai 40° e muovendoci verso valori inferiori non vi sono più massimi di intensità per cui la luce proveniente da tale regione non mostrerà alcuna prevalenza di qualche colore sugli altri. Ciò spiega un’ultima caratteristica associata all’arcobaleno ossia la maggiore luminosità del cielo nelle zone sottostanti l’arco del primario: in effetti questa luminosità biancastra è generata dalla sovrapposizione dei raggi diffusi ad angoli minori dell’angolo di arcobaleno del violetto e, a tale luminosità, contribuiscono in modo sostanzialmente uniforme tutte le lunghezze d’onda del visibile. Le foto 3, 5, 6, 7 e 10 manifestano tutte questa maggiore luminosità del cielo entro il primario.
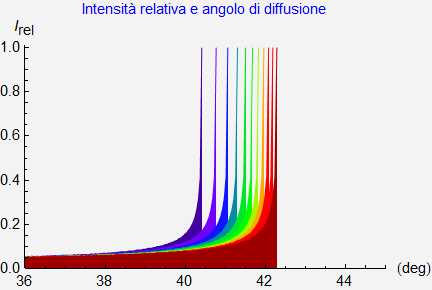
Figura 36. Distribuzione dell’intensità al variare dell’angolo di diffusione.

Foto 10. Zona luminosa chiara al di sotto del primario (sv.wikipedia.org/wiki/Regnb% C3 % A5ge).
Bibliografia e siti web
[1] http://www.philiplaven.com/p20.html
[2] M. Minnaert, The Nature of Light and Colour in the Open Air, Dover, 1954
[3] R. Greenler, Rainbows, Halos, and Glories, Cambridge Univerity Press, 1980
[4] H. C. van de Hulst, Light Scattering by Small Particles, Dover, 1981
[5] E. Dereniak, T. Dereniak, Geometrical and Trigonometric Optics, Cambridge University Press, 2008
[6] H. M. Nussenzweig, L'arcobaleno, Le Scienze, Agosto 1977
[7] http://www.atoptics.co.uk/
[8] http://www.schulphysik.de/ntnujava/Rainbow/rainBow.html
[9] http://mysite.du.edu/~jcalvert/astro/bow.htm

Foto 11. Arcobaleno e archi soprannumerari (www.memic.net)
Ritorna alla pagina di presentazione