L’ITIS J.C. MAXWELL di Nichelino partecipa alla mostra interattiva promossa dalla Provincia di Torino

“Il bello della scoperta”

- Progetto Science Center dedicata alle più belle scoperte scientifiche nel campo della fisica

La mostra si terrà a Nichelino nel salone incontri dell’ ITIS MAXWELL

dal 17-29 ottobre 2005

Referente per la scuola del progetto e della mostra Prof. Bardi Francesco

E’ data la possibilità di proporre agli allievi la realizzazione un nuovo exhibit, relativo ad un esperimento non ancora presente, con la quale arricchire la mostra stessa. Tra gli esperimenti ideati dalle scuole, che avranno riscosso il maggior gradimento del pubblico nel corso della esposizione ad aprile al Lingotto , verrà istituito un premio.

Sono dieci gli esperimenti più votati e attorno ai quali lo Science Center della Provincia di Torino ha costruito la sua mostra.

La top ten copre più di 2000 anni di storia della fisica e comprende scienziati noti e meno noti al grande pubblico:

1. L'esperimento della doppia fenditura di Young applicato all'interferenza da elettrone singolo

2. Galileo e la caduta dei gravi

3. Millikan e l'esperimento per la misura della carica dell'elettrone

4. Newton e la decomposizione dei colori della luce solare con il prisma

5. Young e l'esperimento dell'interferenza della luce

6. Cavendish e l'esperimento per la misura della costante di

gravitazione con la bilancia di torsione

7. Eratostene e la misura della circonferenza della Terra

8. Galileo e l'esperimento del piano inclinato

9. Rutherford e la scoperta del nucleo

10. Il pendolo di Foucault

La mostra si articola in tre sezioni:

-Divulgativa illustrativa – pannelli illustranti gli esperimenti

-Sperimentale – riproduzione di alcuni esperimenti

-Didattica – laboratori didattici di approfondimento dei dieci esperimenti

Gli esperimenti che possono essere attivati direttamente dai visitatori sono:

-La caduta dei gravi di Galileo. Il famoso esperimento viene riproposto attraverso un exhibit composto da una struttura contenente due tubi in plexiglass contenenti all’interno una sfera metallica e una piuma. In un tubo si è creato il vuoto, con assenza d’aria. Il visitatore può capovolgere i tubi e osservare che nel tubo con il vuoto i due oggetti, pur con pesi enormemente diversi, cadono contemporaneamente.

-Accelerazione sul piano inclinato di Galileo. Per dimostrare questa scoperta, l’exhibit è composto da uno scivolo da parco giochi. Nei fianchi dello scivolo sono sistemati dei sensori a raggi infrarossi che inviano via radio ad una centralina di elaborazione i dati dell’accelerazione del passaggio delle persone che utilizzano lo scivolo. Su un display a led compaiono i relativi dati.

-Scomposizione della luce di Newton. Questo exhibit è allestito con un classico banco ottico con pareti che tendono ad oscurare lo spazio dell’esperimento. Sul piano è sistemata una fonte luminosa di luce bianca che colpisce un prisma in plexiglass, e sulla parete opposta si forma la famosa scomposizione nei colori componenti l’iride.

-Il fenomeno della interferenza della luce di Young. Anche per questo esperimento si utilizza un banco ottico sul quale è collocato un interferometro con il quale è evidenziata la natura ondulatoria della luce ed il fenomeno della diffrazione.

-La costante gravitazionale di Cavendish. Viene riproposta la bilancia di torsione che registra il moto gravitazionale tramite l’accelerazione di due sfere registrate con un indice luminoso, il cui movimento è rilevato su una parete opposta.

-Scoperta del nucleo dell’atomo di Rutherford. E’ allestito un modello composto da una scatola oscurata con pareti mobili di diversa conformazione. Sulle diverse pareti con superfici riflettenti viene “sparato” un raggio laser, che riflette la sua luce diversamente in ragione delle diverse superfici.

01 L'esperimento della doppia fenditura applicato all'interferenza da elettrone singolo

E' italiano l'esperimento più bello

A differenza di tutti gli altri esperimenti in classifica, “l’interferenza da doppia fenditura di singolo elettrone” non ha un “papà” unico e riconosciuto: alla sua realizzazione non è associato il nome di nessuno scienziato famoso.

Questa esperienza dimostra un concetto chiave della meccanica quantistica, cioè che a livello microscopico particelle materiali come gli elettroni si comportano anche come onde. Fu ideato e pensato nel dettaglio ben prima che fosse tecnicamente possibile realizzarlo. Era considerato un Gedankenexperiment, un esperimento concettuale, uno di quelli importanti nella storia della fisica dei quanti. Ancora nelle sue lezioni tenute all’inizio degli anni ’60, il premio Nobel Richard Feynman affermava che era impossibile svolgerlo ad una scala sufficientemente piccola da essere interessante. Proprio nel 1961, Claus Jönsson dell’Università di Tubinga, aveva realizzato l’esperimento con alcuni elettroni, senza però destare particolare attenzione.

La prova decisiva però doveva mostrare che il fenomeno dell’interferenza si verifica anche con un solo elettrone. Physics World, nel riportare i risultati del sondaggio, attribuisce il merito del primo esperimento di questo tipo al giapponese Akira Tonomura, che lo realizzò con il suo gruppo nel 1989. La rivista nel maggio 2003 è stata però costretta a pubblicare alcune lettere di smentita, in cui viene chiarito che furono tre italiani, Pier Giorgio Merli, GianFranco Missiroli e Giulio Pozzi, a portare a termine per primi l’esperimento con un singolo elettrone, nel 1974.

I tre ricercatori, che ancora oggi lavorano a Bologna, studiavano all’epoca le applicazioni pratiche dell’interferometria, usata per misurare lunghezze sfruttando il fenomeno dell’interferenza. Non trascurarono però l’aspetto didattico e storico delle loro ricerche. Solo oggi il loro merito viene giustamente riconosciuto.

L'esperimento: l'elettrone sulla cresta dell'onda

L’interferenza è un fenomeno caratteristico di tutti i tipi di onde, da quelle sonore a quelle del mare. È quello che succede ad esempio quando lanciate due sassi in uno stagno. Le piccole onde che si formano nell’acqua si sommano in altezza in alcuni punti e si annullano a vicenda in altri.

Un effetto analogo avviene per un raggio di luce che passa attraverso due fenditure affiancate, come dimostrò Thomas Young: oltre le aperture non compaiono due strisce luminose verticali, ma una serie di frange alternativamente chiare e scure. E la stessa cosa succede agli elettroni.

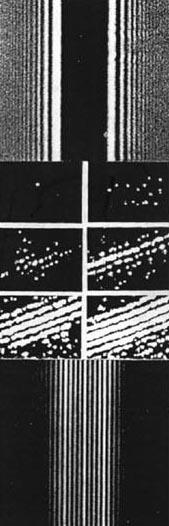Nell’esperimento il fascio di elettroni viene fatto passare attraverso due fenditure e raccolto su uno schermo sensibile. Sullo stesso non si osservano solo due chiazze in corrispondenza delle due fenditure ma compaiono striscie alternativamente chiare e scure caratteristiche della figura di interferenza. Questo fenomeno era già stato dimostrato da Claus Jönsson nel 1961. Ciò che mancava era mostrare che il fenomeno veniva prodotto anche dal passaggio di un solo elettrone per volta e che quindi il comportamento ondulatorio non era da associarsi al fascio ma al singolo elettrone.

Merli, Missiroli e Pozzi, per portare a termine l’esperimento, avevano a disposizione un potente microscopio elettronico che per la prima volta poteva rilevare il passaggio di un singolo elettrone. Consapevoli dell’importanza concettuale che rivestiva la realizzazione dell’interferenza di singolo elettrone tentarono di mettere in atto il famoso esperimento ideale della fisica quantistica. Non solo. Filmarono la formazione delle frange di interferenza e, partendo da questo materiale, realizzarono un premiato documentario scientifico.

Quelle immagini mostrano che le frange si formano allo stesso modo se si aumenta costantemente il numero di elettroni che passano o se viene registrato in tempi successivi l’effetto di un singolo elettrone: è la conferma che un elettrone ha qualcosa in comune con un’onda.

Per vedere l'animazione dell'esperimento dal sito dei ricercatori bolognesi, cliccare qui

02 Galileo e la caduta dei gravi

Sulla Torre di Pisa

Galileo comincia a studiare il moto di caduta dei corpi all’inizio della sua carriera, quando fra il 1589 e il 1592 tiene a Pisa la cattedra di matematica, e perfeziona la sua spiegazione del fenomeno durante il resto della sua vita, fino agli ultimi anni trascorsi in isolamento. L’episodio di Galileo che sperimenta le sue ipotesi lasciando cadere corpi diversi dalla cima della Torre di Pisa è riportato dal suo allievo Vincenzo Viviani, ma gli storici mettono in dubbio che sia realmente accaduto, anche perché avrebbe probabilmente mostrato conclusioni opposte a quelle che Galileo voleva.

Da Aristotele in poi si riteneva che la velocità di caduta di un corpo dipendesse dal suo peso. In pratica che, lasciando cadere una biglia di piombo e una uguale di sughero, la prima sarebbe arrivata a terra più presto. Se fate la prova, verificherete che succede proprio così! Galileo però si era accorto che nella realtà è determinante il mezzo in cui cadono i corpi, cioè che ad esempio in acqua il distacco fra le due biglie è maggiore che nell’aria. Nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze concluderà che: “(...) se si levasse totalmente la resistenza del mezzo, tutte le materie discenderebbero con eguali velocità”.

Oggi sappiamo che l’attrito dell’aria modifica la velocità di caduta dei corpi, a seconda della loro forma e del loro peso. In effetti Galileo non ha modo di verificare direttamente la sua ipotesi perché non può realizzare una situazione in cui l’attrito dell’aria sia trascurabile. Dimostra però con un ragionamento per assurdo che la teoria aristotelica è contraddittoria e studia invece la parte iniziale del moto, in cui si passa dalla velocità nulla a quella di regime, mettendo in evidenza il ruolo dell’accelerazione, fino ad allora completamente trascurato.

La luna fornisce la prova

Per confutare la teoria aristotelica secondo cui la velocità di caduta di un corpo dipende dal suo peso, Galileo propone un ragionamento di questo tipo: “Se abbiamo due pesi, uno da 10 e uno da 5 chilogrammi, secondo Aristotele quello da 10 kg cadrà il doppio più veloce dell’altro. Ma sempre secondo Aristotele, se uniamo i due corpi, quello da 10 kg, dato che di natura va più veloce, tenderà a velocizzare quello da 5 kg; quest’ultimo, invece, farà rallentare quello da 10 kg, e si raggiungerà quindi una velocità intermedia. D’altra parte si può anche pensare che, se uniamo i due corpi, il peso totale sarà 15 kg e quindi di natura l’unione di questi corpi andrà ad una velocità superiore alla velocità del peso di 10 kg e non ad una velocità intermedia”. Le due conclusioni, logicamente corrette, portano a verità contrastanti. Se ne deve concludere che l’ipotesi iniziale è errata.

Ma la bellezza del risultato di Galileo non sta tanto nell’esperimento mentale, quanto nella capacità dello scienziato di studiare il fenomeno della caduta isolandolo da tutti gli elementi “di disturbo” che non sono necessari alla sua comprensione, per estrapolare i risultati in una condizione ideale. Questo modo di operare è caratteristico del metodo scientifico moderno.

La verifica della legge di caduta dei gravi fu riprodotta durante la missione Apollo 15 sulla Luna nel 1971, in assenza di atmosfera e quindi di attrito con l’aria. La piuma e il martello, lasciati cadere nello stesso istante dall’astronauta, giungevano al suolo contemporaneamente, confermando così l’intuizione avuta da Galileo quasi quattro secoli prima.

03 Millikan e l'esperimento per la misura della carica dell'elettrone

Un piccolo cielo stellato

Per misurare la carica di un elettrone, Millikan essenzialmente studia il modo in cui si muovono piccole cariche elettriche fra due piastre metalliche parallele caricate una positivamente e l’altra negativamente tramite una batteria. Per permettere l’osservazione, Millikan perfeziona una tecnica già usata da altri. Mette le due piastre orizzontalmente in un contenitore isolato e ionizza l’aria fra di esse con dei raggi X, in modo da staccare elettroni dagli atomi di aria. Sopra le piastre, inserisce un nebulizzatore, con cui introduce nel contenitore delle goccioline di olio. Queste cadono per gravità e alcune di esse passano attraverso un foro nella piastra superiore. Le cariche elettriche liberate per ionizzazione si attaccano a queste goccioline. Una luce permette di illuminare le gocce e farle apparire allo scienziato, che le osserva attraverso un microscopio, come stelle luminose nel cielo.

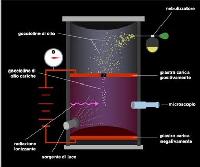
Inizialmente le piastre non sono caricate, così Millikan, misurando il tempo impiegato a percorrere un certo spazio, può calcolare la loro velocità in caduta libera. Poi le piastre vengono caricate con tensioni variabili e, a seconda della carica negativa che hanno acquistato, le gocce vengono più o meno attirate dalla piastra superiore positiva e quindi rallentano la loro caduta fino a rimanere sospese a mezz’aria. Questo succede quando la forza elettrica è uguale a quella di gravità che agisce in verso opposto. Dalla tensione necessaria a fermare la goccia, Millikan può risalire alla sua carica elettrica.

Variando la tensione Millikan fa salire e scendere più volte una singola goccia, che aumenta la sua carica catturando altri elettroni. Millikan osserva che la differenza fra le varie cariche misurate è una costante o un multiplo di essa. Questa costante è proprio il valore dell’unità di carica elettrica elementare, ossia la carica dell’elettrone.

Una scoperta elettrizzante

L’esperimento di Millikan aveva lo scopo di stabilire che la carica elettrica è quantizzata, cioè che è costituita da un’unità elementare e che questa unità è collegata alla natura atomica della materia. Per fare questo era necessario mostrare che la carica elementare non è il risultato di una media calcolata su un grande numero di casi, come è ad esempio per il peso atomico di un elemento. La precisione della misura doveva essere tale da dimostrare che il valore della carica più piccola è sempre costante. La bellezza dell’esperimento di Millikan va quindi oltre il semplice miglioramento di una misura.

Il valore di carica trovato da Millikan era in realtà leggermente inferiore a quello oggi calcolato, perché Millikan utilizzava per la viscosità dell’aria un valore non corretto. Tuttavia, questo numero, inserito nella formula proposta da Niels Bohr per calcolare lo spettro di radiazioni emesse dall’idrogeno, diede la prima conferma sperimentale della teoria dell’atomo quantizzato.

L’esame postumo dei quaderni di laboratorio di Millikan ha però evidenziato che dalla mole dei dati furono eliminati tutti quelli che si discostavano troppo dal valore centrale e che non avrebbero permesso di dire con certezza che c’era un un’unità elementare di carica. Millikan cedette quindi alla tentazione di mostrare solo i risultati che soddisfacevano la sua ipotesi.

La tipologia di esperimento però si è consolidata e non solo è diventata un classico dei laboratori per gli studenti di fisica, particolarmente negli Stati Uniti, ma una versione adattata è stata utilizzata, senza successo, per verificare l’esistenza dei quark, i componenti di protoni e neutroni, che avrebbero carica pari ad un terzo di quella dell’elettrone. Le teorie attuali però ritengono che i quark siano indissolubilmente legati fra loro e che sia impossibile osservarli singolarmente.

04 Newton e la decomposizione dei colori della luce solare con il prisma

Scomporre la luce

Newton comincia gli esperimenti sui colori e la luce nel periodo in cui, per sfuggire alla peste, si ritira nella casa di famiglia in campagna. A quell’epoca si pensa che i colori siano un misto di luce e di ombra e che i prismi in qualche modo colorino la luce.

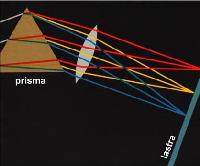Newton si procura un prisma triangolare e lo mette attraverso un raggio di sole. Nei loro esperimenti Cartesio, Hooke e Boyle avevano posto uno schermo vicino alla faccia del prisma da cui usciva la luce e avevano osservato un miscuglio di colori. Newton realizza che per ottenere uno spettro ben visibile, deve allontanare notevolmente lo schermo. Sfrutta tutta l’ampiezza del suo studio, dalla finestra al muro, per vedere proiettati tutti i colori separati. Ma per provare che non è il prisma a colorare la luce, Newton mette a punto un Experimentum crucis, l’esperimento decisivo. Sul percorso del suo spettro mette uno schermo in cui ha tagliato un fessura sottile, in modo da far passare solo il raggio verde. Quindi fa passare questo raggio in un secondo prisma. Se il prisma colora la luce, allora il raggio verde deve uscirne di colore diverso. Il raggio invece rimane verde, non modificato dal prisma. Newton così dimostra che i colori sono le varie componenti della luce che il prisma semplicemente separa. Facendo passare tutto lo spettro attraverso il secondo prisma messo in modo opportuno, Newton riesce infatti a ricomporre il fascio di luce bianca.

Applicando rigorosamente il metodo scientifico Newton raccoglie una gran quantità di dati, ottenuti combinando in vari modi i prismi. Ne conclude che i raggi vengono rifratti, ossia piegati, nel passaggio dall’aria al vetro e viceversa, in modo diverso a seconda del loro colore e che “l’indice di rifrazione è sì costante per due determinati mezzi, qualunque sia l’angolo d’incidenza, ma cambia col cambiare del colore della luce”.

Tutti i colori dell'arcobaleno

Un arcobaleno è il risultato di un prisma naturale in grande scala. Le gocce d’acqua sospese in aria possono comportarsi in modo simile ad un prisma, separando i colori della luce per produrre lo spettro che è appunto l’arcobaleno. La luce viene piegata, o meglio rifratta, nel passaggio da un materiale ad un altro, come ad esempio fra l’aria e il vetro o l’aria e l’acqua. I differenti colori della luce, che oggi sappiamo corrispondere a diverse frequenze dell’onda luminosa, vengono rifratti in modo diverso. Il violetto, che ha la frequenza più alta, viene piegato di più, mentre il rosso è la componente che viene deviata di meno. A causa di questa differente rifrazione, i raggi di colori diversi escono separati. E se ci troviamo nella posizione giusta, riusciamo a vedere la luce rifratta dalle gocce d’acqua formare l’arcobaleno.

Newton mostrò che anche una cosa in apparenza semplice come un raggio di luce, può rivelarsi meravigliosamente complessa.

Fu Newton stesso ad identificare nello spettro i sette colori. Si tratta in realtà di una divisione artificiosa, perché all’interno dello spettro i colori cambiano in modo continuo e non netto.

Newton rimandò la trattazione completa di tutti i risultati riguardanti l’ottica e la luce per evitare polemiche con altri scienziati. Nel 1704, ormai alla fine della carriera, pubblicò l’Opticks, in cui fra l’altro si mostrava favorevole alla ipotesi che la luce sia fatta di corpuscoli piuttosto che di onde. La sua posizione influenzerà decisamente il dibattito sulla natura della luce che si concluderà solo agli inizi del XX secolo, quando la teoria dei quanti mostrerà che la luce è contemporaneamente onda e particella.

05 Young e l'esperimento dell'interferenza della luce

La luce è fatta di onde

“L’esperimento di cui sto per parlare (…) può essere ripetuto con grande facilità, purché splenda il sole e con una strumentazione che è alla portata di tutti”. Così Thomas Young, parlando il 24 novembre 1803 alla Royal Society di Londra, comincia la sua descrizione dello storico esperimento di interferenza della luce.

Ecco come lo aveva realizzato: un raggio di sole veniva deviato con uno specchio in modo da entrare orizzontale nella stanza. Successivamente era reso molto sottile facendolo passare per un piccolo foro creato in una superficie opaca. Quindi il raggio veniva diviso attraversando due fenditure strette e vicine. Nelle sue prime prove Young in realtà non usò una “doppia fenditura” ma un foglietto che con il suo spigolo sottile separava in due il raggio. Dalle fenditure la luce infine colpiva uno schermo. Young osservò che sullo schermo non comparivano due immagini luminose corrispondenti alla forma delle fenditure, ma che i raggi si allargavano, si sovrapponevano e nell’area di sovrapposizione formavano delle bande luminose alternate a zone d’ombra. Come le onde nate in due punti diversi di un lago, incontrandosi, sommano la loro altezza in alcuni punti e si annullano a vicenda in altri.

“Neanche i più prevenuti negheranno” osservò Young nel suo discorso tenuto davanti ad un’assemblea di scettici, “che le frange osservate sono prodotte dall’interferenza di due frazioni della luce”. La conferenza, pubblicata l’anno successivo nelle Philosophical Transactions of the Royal Society e destinata a diventare un classico, propone, con un linguaggio brillante, la prima prova chiara e decisiva delle proprietà ondulatorie della luce.

Dato che la distanza fra le frange di interferenza dipende dalla lunghezza d’onda, l’esperimento di Young offrì anche la prima misura diretta della lunghezza d’onda della luce.

Gli ologrammi e la relatività di Einstein

La natura della luce, ossia se la luce sia fatta di particelle o se sia un’onda, è stata una delle più affascinanti questioni scientifiche dei secoli XVII e XVIII. Young, con le sue figure di interferenza, alla lunga aveva convinto molti scienziati della validità dell’ipotesi ondulatoria. Ma agli inizi del XX secolo furono osservati fenomeni che non erano in accordo con questo schema. Il più noto è l’effetto fotoelettrico, che si manifesta quando una sostanza colpita dalla luce emette elettroni. Einstein lo spiegò ipotizzando che la luce sia fatta di quantità elementari non divisibili: “quanti” di luce, battezzati fotoni. La meccanica quantistica negli anni ’20 e ’30 stabilirà che la natura materiale dei fotoni convive con quella di onda.

Oggi per mostrare l’interferenza della luce si usa il laser, che permette di ottenere facilmente il tipo di luce adatta. L’interferenza realizzata con i laser viene usata per produrre gli ologrammi, come quelli che compaiono sulle carte di credito e che danno l’immagine tridimensionale di un oggetto.

Si basano sull’interferenza della luce anche gli interferometri, strumenti che misurano con precisione lunghezze o variazioni di lunghezza. Se il percorso del raggio luminoso cambia, l’interferometro lo rileva, anche su grandi distanze, perché si modificano le figure di interferenza. Dispositivi basati su questo principio vengono utilizzati per seguire i movimenti delle placche geologiche sulla superficie terrestre.

L’interferometro di Michelson e Morley è stato utilizzato nel 1887 per dimostrare che l’etere, il “supporto materiale” in cui avrebbe dovuto viaggiare la luce, non esiste. Questo esperimento ha avuto un’influenza capitale sulla teoria della relatività di Einstein, in particolare sull’ipotesi che la velocità della luce nel vuoto sia costante.

06 Cavendish e la misura della costante di gravitazione con la bilancia di torsione

Una bilancia per la Terra

Questo è l’esperimento con cui Henry Cavendish calcolò la densità media della Terra. È ricordato però come la misura della costante di gravitazione universale G, quel numero che compare nella legge di Newton in cui è stabilita la forza con cui si attraggono due masse.

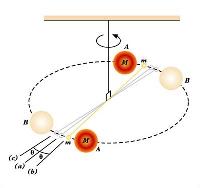L’esperimento si basa su uno strumento chiamato bilancia di torsione. Si tratta di un’asta rigida di legno con alle estremità due piccole sfere di piombo. Questo “manubrio” è appeso in posizione orizzontale tramite un filo sottile. Per impedire che le correnti d’aria muovessero l’asta, Cavendish chiuse la sua bilancia in una cassa di legno. Dall’esterno avvicinò alle estremità del manubrio due sfere più grandi e pesanti, ponendole da parti opposte rispetto all’asta. Per limitare i fattori che disturbavano la misura, Cavendish tenne chiusa la stanza con gli strumenti, muovendo le sfere grandi dall’esterno e osservando da fuori con un cannocchiale. Come aveva stabilito Newton, due corpi qualsiasi si attraggono con una forza che aumenta in proporzione alle loro masse e quanto più essi sono vicini. Le sfere grandi, fissate, attiravano quindi le sfere piccole e facevano ruotare leggermente il manubrio. Il filo, messo in torsione, si opponeva a questa rotazione. Cavendish ripetè l’operazione mettendo le sfere grandi dall’altro lato della cassa in modo che attirassero il manubrio in senso opposto. Dalle oscillazioni dell’asta ricavò la posizione di equilibrio in cui la forza di attrazione gravitazionale fra le sfere uguagliava quella che si opponeva alla torsione del filo. Misurando l’angolo di cui l’asta ruotava spostando le sfere da un lato all’altro, Cavendish fu in grado di calcolare G. Da questo valore ricavò la massa della Terra e dividendola per il suo volume ne ottenne la densità media. Questa risultò 5,448 volte quella dell’acqua, un valore che è solo dell’1,3% più basso di quello oggi accettato.

Una costante può cambiare?

Perché è importante misurare quanto vale la costante di gravitazione universale G? Innanzitutto il valore di G ci ha permesso di calcolare la massa della Terra, della Luna e degli altri pianeti. La forza gravitazionale, poi, è fondamentale nelle teorie sull’origine e la struttura dell’Universo. Per questo sarebbe importante sapere se G è realmente una costante o se cambia con il tempo, se dipende dallo stato fisico e chimico delle masse o dalla loro temperatura. Finora le misure sperimentali non hanno dato nessuna certezza, anche perché è difficile misurare G con grande precisione. Rispetto ad altre costanti fisiche, la precisione di cui disponiamo non è eccezionale perché G ha un valore molto piccolo e di conseguenza la forza che si esercita fra le masse in laboratorio è molto debole. La ricerca sperimentale in questo campo quindi prosegue migliorando i risultati ma continua ad utilizzare, con qualche correzione, lo stesso metodo messo in pratica da Cavendish.

Di Cavendish si dice che sia stato il primo a “pesare” la Terra, perché sapendo il valore di G aveva potuto ottenere dalla legge di Newton la massa del pianeta. Dividendo poi questa massa per il volume corrispondente, aveva calcolato la sua densità media. Il raggio terrestre necessario a calcolare il volume era stato ottenuto per la prima volta duemila anni prima da Eratostene. La densità media delle rocce della superficie terrestre è molto inferiore al valore di densità ottenuto da Cavendish, quindi questo ci permette di concludere che la parte interna della Terra deve contenere materiali di densità maggiore: l’esperimento di Cavendish in definitiva ci dà informazioni anche sul nucleo interno della Terra!

07 Eratostene e la misura della circonferenza della Terra

Al tempo di Eratostene era noto che a Siene – l’odierna Assuan nel sud dell’Egitto – a mezzogiorno del solstizio d’estate il Sole si trova circa allo zenit, il punto più alto del cielo. In quel momento il Sole era così a picco che poteva essere visto anche dall’interno di un pozzo molto profondo. Partendo da questa conoscenza, Eratostene ha un’idea: ad Alessandria pianta un bastone, di cui conosce l’altezza, e misura l’ombra che proietta a terra. Con questi dati e usando un po’ di trigonometria, calcola l’angolo che i raggi del Sole formano con la superficie terrestre.

Per confrontare la sua misura, Eratostene sa che deve effettuarla alla stessa ora del giorno di solstizio: quello stesso istante in cui a Siene il bastone non proietta alcuna ombra. Quindi, per semplicità, considera Alessandria esattamente a Nord di Siene, cosa per altro non lontana dal vero. Eratostene fa altre due ipotesi: che la Terra sia perfettamente sferica e che i raggi del Sole arrivino a noi tutti paralleli fra loro.

La sua deduzione è questa: l’angolo che l’ombra forma con il bastone è uguale all’angolo al centro della Terra in corrispondenza dello “spicchio” compreso fra Alessandria e Siene. A questi dati empirici aggiunge la conoscenza della distanza fra le due città, riportata da viaggiatori e commercianti.

Ora Eratostene ha tutti i dati per calcolare la circonferenza terrestre. Gli basta risolvere questa proporzione:

DISTANZA SIENE-ALESSANDRIA : CIRCONFERENZA DELLA TERRA = ANGOLO TRA BASTONE E OMBRA : 360°

Il risultato della misura, riportato nell’opera Sulla misurazione della Terra purtroppo andata perduta, è di 250.000 stadi. Per quanto non ci sia un parere univoco su quanto valesse esattamente lo stadio, unità di lunghezza dell’epoca, il valore ottenuto da Eratostene è comunque buono, se non sorprendente, rispetto ai 40.075 chilometri misurati oggi.

La misura di tutte le cose

Un uomo che, senza muoversi da casa, avendo a disposizione semplici strumenti e utilizzando il suo ingegno, più di 2200 anni fa calcola la dimensione della Terra con uno scarto dell’1% rispetto al valore reale: ecco la potenza e l’eleganza dell’esperienza di Eratostene. Altro che Terra piatta: i greci del terzo secolo avanti Cristo erano convinti della sfericità del nostro pianeta ed erano arrivati a misurare la lunghezza della sua circonferenza.

Ed Eratostene aveva calcolato anche la distanza del Sole e della Luna, utilizzando dati ricavati durante le eclissi lunari.

Il metodo utilizzato da Eratostene per arrivare alla lunghezza del meridiano terrestre consisteva nel calcolare a quale parte della circonferenza terrestre corrispondesse la distanza fra Siene e Alessandria e ricavarne, in proporzione, l’intero meridiano. Lo stesso metodo “proporzionale” fu utilizzato duemila anni dopo per stabilire la lunghezza del metro.

Alla fine del XVIII secolo fu deciso in Francia che l’unità di misura della lunghezza sarebbe stata equivalente alla milionesima parte del quarto di meridiano passante per Parigi. Per ottenere la massima precisione possibile, fu organizzata una spedizione scientifica a capo degli astronomi Delambre e Méchain, con il compito di estrapolare dalla misura della distanza delle città di Barcellona e Dunkerque la lunghezza del meridiano prescelto. Le peripezie della spedizione, durata ben sette anni, si conclusero con una conferenza internazionale di scienziati che sancì l’entrata in vigore del sistema metrico decimale.

08 Galileo e l'esperimento del piano inclinato

Un quarto della lunghezza in metà tempo

Con l’esperimento del piano inclinato Galileo modifica radicalmente l’idea aristotelica del moto, concentrando l’attenzione sull’accelerazione, un livello del moto ignorato da Aristotele e dalla maggior parte dei suoi successori.

Ecco come Galileo stesso lo descrive nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze: “In un regolo, o vogliàn dir corrente, di legno, lungo circa 12 braccia, e largo per un verso mezzo braccio e per l’altro 3 dita, si era in questa minor larghezza incavato un canaletto, poco più largo d’un dito; tiratolo drittissimo, e, per averlo ben pulito e liscio, incollatovi dentro una carta pecora zannata e lustrata al possibile, si faceva in esso scendere una palla di bronzo durissimo, ben rotondata e pulita”. Con questi accorgimenti Galileo vuole rendere trascurabili gli effetti dell’attrito. “Elevando sopra il piano orizzontale una delle estremità (del regolo) un braccio o due ad arbitrio, si lasciava (…) scendere per il detto canale la palla, notando (…) il tempo che consumava nello scorrerlo tutto, replicando il medesimo atto molte volte per assicurarsi bene della quantità del tempo (…). Fatta e stabilita precisamente tale operazione, facemmo scender la medesima palla solamente per la quarta parte della lunghezza di esso canale; e misurato il tempo della sua scesa, si trovava sempre puntualissimamente esser la metà dell’altro”. Ripetendo la misura per distanze diverse, Galileo deduce che lo spazio percorso è sempre proporzionale al quadrato del tempo impiegato a percorrerlo. In altri termini, se i tempi sono rappresentati da 1, 2, 3, 4, 5… gli spazi percorsi sono rispettivamente rappresentati da 1, 4, 9, 16, 25… Questa è la prima descrizione del tipo di moto definito, da Galileo in poi, “uniformemente accelerato”.

Misurare il tempo senza orologi

I risultati dell’esperimento con il piano inclinato sono eccezionali nonostante la semplicità dell’apparato sperimentale. Bisogna sottolineare il fatto che all’epoca di Galileo non esistevano orologi né cronometri e che i metodi disponibili non avevano la precisione necessaria a calcolare il tempo di caduta della sfera.

Per risolvere questo problema, Galileo progetta e realizza un orologio ad acqua, che presenta in questo modo nei suoi Discorsi e dimostrazioni matematiche intorno a due nuove scienze: “Quanto poi alla misura del tempo, si teneva una gran secchia piena d’acqua, attaccata in alto, la quale per un sottil cannellino, saldatogli nel fondo, versava un sottil filo d’acqua, che s’andava ricevendo con un piccol bicchiero per tutto ‘l tempo che la palla scendeva nel canale e nelle sue parti: le particelle poi dell’acqua, in tal guisa raccolte, s’andavano di volta in volta con esattissima bilancia pesando, dandoci le differenze e proporzioni de i pesi loro le differenze e proporzioni de i tempi; e questo con tal giustezza, che, come ho detto, tali operazioni, molte e molte volte replicate, già mai non differivano d’un notabil momento”.

Con questo strumento Galileo riesce a rivelare che lo spazio percorso dalla sfera di metallo non è proporzionale al tempo impiegato a percorrerlo, come avrebbe detto Aristotele, ma al quadrato del tempo. Gli strumenti di misura di Galileo ricostruiti fedelmente ai giorni nostri hanno mostrato che Galileo aveva potuto ottenere l’accuratezza che dichiara.

Poiché Galileo capisce che lo stesso tipo di moto caratterizza la sfera sul piano inclinato e in caduta libera, con il suo strumento riesce a “vedere a rallentatore” il moto accelerato, studiandolo in una situazione in cui l’accelerazione è inferiore a quella di gravità.

09 Rutherford e la scoperta del nucleo

Un modello ancora attuale

Gli ultimi anni del XIX secolo sono quelli della scoperta e dello studio pionieristico della radioattività, dapprima con Bequerel, poi con i coniugi Curie. Ernest Rutherford si inserisce in questo filone, con l’intenzione di capire che cosa succeda esattamente nei decadimenti, quelle reazioni che avvengono nei nuclei delle sostanze radioattive. Scopre che, fra le diverse radiazioni, quelle con più energia sono di tipo a e che queste sono costituite da atomi di elio con carica elettrica positiva. Inventa allora insieme al suo assistente Hans Geiger un “contatore” in grado di rivelare il passaggio di una singola particella a. Con l’intenzione di studiare il modo in cui questa radiazione interagisce con la materia, chiede a Geiger di contare, per ogni angolazione, il numero di particelle a che viene deviato da un sottile strato di materiale. Geiger, che insegna agli studenti le tecniche sperimentali, si fa aiutare dal laureando Ernest Mardsen per misurare le deviazioni prodotte dalle superfici metalliche. Marsden osserva che, mentre molte particelle passano, alcune vengono rimbalzate completamente all’indietro, anche soltanto con un sottile strato d’oro. Dirà Rutherford: “E’ come se una palla di cannone sparata contro un foglio di carta velina tornasse indietro”.

Nel 1911 Rutherford deduce da queste osservazioni che, al contrario di quanto si riteneva allora in base al modello di J. J. Thompson, la massa di un atomo è concentrata in un nucleo migliaia di volte più piccolo dell’atomo stesso.

Il giovane fisico danese Niels Bohr, interessato a questi risultati, darà la necessaria completezza al modello atomico che sarà chiamato con i nomi dei due scienziati. Un modello ancora valido oggi, eccezion fatta per alcune correzioni legate alla meccanica quantistica.

L'atomo non è un "panettone"

Qualcuno ha detto che Rutherford sta all’atomo come Darwin all’evoluzione, Newton alla meccanica, Faraday all’elettricità e Einstein alla relatività. La sua teoria sulla struttura atomica ha dato una svolta alla nostra concezione della realtà a livello microscopico. Da allora è chiaro che l’atomo non è un “panettone” caricato positivamente, in cui qua e là, si trovano, sparsi come uvette, gli elettroni con la loro carica elettrica negativa. Al contrario, sappiamo che la materia è costituita in gran parte di vuoto. Se tutti gli elettroni dei nostri atomi cadessero improvvisamente sul nucleo, noi ci ridurremmo alle dimensioni di un granello di sabbia!

Rutherford, misurando un decadimento radioattivo, si rese conto però che nel minuscolo nucleo c’era un’energia sorprendente: milioni di volte superiore a quella dei legami chimici che tengono insieme le molecole. Nel 1916, durante la Prima Guerra Mondiale, Rutherford disse: “Spero che l’uomo non riesca a estrarre questa energia finché non avrà imparato a vivere in pace con i suoi simili”. Hiroshima e Nagasaki avrebbero mostrato quanto fossero fondati i suoi timori.

Da Rutherford in poi, la tecnica del “bombardamento”, chiamato dai fisici “scattering”, è molto utilizzata per l’esplorazione del mondo subatomico. Gli acceleratori sono costruiti proprio per portare particelle come elettrone e protone a energie elevate e farle scontrare fra di loro o contro un bersaglio fisso di atomi di un certo elemento. In questo modo si possono creare nuove particelle e ricavare informazioni preziose sulla forma del “bersaglio” e sul tipo di interazione, a partire dalla traiettoria e dall’energia dei prodotti della collisione.

10 Il pendolo di Foucault

L’esperimento con cui Leon Foucault dimostra la rotazione della Terra è stato realizzato dal fisico francese circa centocinquant’anni fa. Egli, volendo studiare la proprietà dei pendoli di oscillare sempre nello stesso piano, ne costruisce uno lungo un paio di metri nella sua casa di Parigi. La notte dell’8 gennaio 1851 osserva che il piano di oscillazione ruota lentamente in senso orario. Ripetendo più volte la prova nei giorni successivi con fili più lunghi e masse maggiori, lo scienziato si convince che non è il pendolo a ruotare, ma la Terra sotto di lui!

A marzo Foucault esegue l’esperimento in pubblico nel Pantheon con un pendolo lungo 67 metri e una massa di 28 chilogrammi, suscitando un’enorme impressione.

Ma come si può spiegare il moto del pendolo? Immaginate di farne oscillare uno esattamente sopra il Polo Nord. Lo spostate un po’ dalla sua posizione di equilibrio e poi lo lasciate andare da fermo. Come Foucault sapeva, il suo piano di oscillazione non varierà nel tempo, mentre la Terra continua il suo moto di rotazione da Ovest verso Est passando per il Sud. A voi che vi muovete insieme alla Terra, sembrerà invece che sia il pendolo a ruotare nel verso opposto, in senso orario. Per fare un giro completo impiegherà esattamente un giorno. Spostandovi più a Sud, potreste verificare che il periodo di rotazione (il tempo impiegato a fare un giro) aumenta. Arrivando all’Equatore, a parte temperature più miti, troverete che il pendolo non ruota affatto! Gli abitanti dell’emisfero australe vedono invece ruotare il pendolo in senso antiorario.

Il pendolo di Foucault, reso celebre dall’omonimo romanzo di Umberto Eco, nel Pantheon di Parigi impiegava circa 31 ore e 45 minuti per compiere una rotazione completa, mentre a Torino gira in 34 ore circa.

Una dimostrazione facile. In teoria

Tutti sanno che la Terra ruota su se stessa. Ma se vi chiedessero di dimostrarlo, sareste in grado di farlo? Non è poi così semplice. Pensate che poco più di centocinquant’anni fa, tre secoli dopo che Copernico aveva smentito Aristotele riguardo alla fissità della Terra nell’Universo, nessuno aveva ancora saputo mostrare in modo convincente la rotazione terrestre.

Foucault ci riuscì sfruttando la sua curiosità e la sua ingegnosità. La bellezza dell’esperienza del pendolo sta proprio nell’aver svelato in modo plateale e comprensibile ciò che molti avevano cercato per anni.

Circa due secoli prima un allievo di Galileo, Vincenzo Viviani, aveva osservato lo stesso fenomeno ed era arrivato alla conclusione opposta, che cioè ci dovesse essere una forza che faceva ruotare il piano di oscillazione del pendolo.

In realtà la causa che lo fa variare, la rotazione terrestre, è la stessa che nel nostro emisfero devia verso destra i venti e le correnti oceaniche mentre li fa girare verso sinistra nell’emisfero Sud, influenzando così il clima. L’effetto deve essere tenuto in considerazione anche dai piloti di aereo per non atterrare a Ovest del punto previsto.

La proprietà di mantenere invariato il proprio piano di rotazione fu sfruttata da Foucault anche per ideare il giroscopio, strumento che sta alla base della girobussola, il principale sistema di navigazione marittima e aerea usato fino ai giorni nostri, sostituito solo parzialmente dal GPS. Si tratta essenzialmente di una trottola in rapida rotazione, che, proprio come il giocattolo, tende a resistere a cambiamenti del proprio asse. Il giroscopio, attraverso un quadrante graduato, può quindi indicare le deviazioni, rispetto alla posizione iniziale, del mezzo su cui è installato.

Dove sta "il bello della scoperta"?

I lettori di Physics World che hanno risposto al sondaggio, hanno offerto una varietà di ragioni per le loro scelte.

Una di queste indicava come aspetto della bellezza il “potere di trasformazione” di un esperimento: la sua capacità di cambiare il modo di pensare ed il comportamento di chi lo realizza per la prima volta e di chi lo riproduce, anche se è già preparato al risultato.

Qualcun altro ha parlato di bellezza di un esperimento in termini di “economia”, ossia con quanta efficacia e immediatezza la prova renda esplicito un risultato. L’economicità si può riferire sia alla semplicità dell’apparato sperimentale sia al modo in cui presenta un risultato significativo, oppure ad entrambi.

Altri criteri menzionavano la bellezza di alcuni strumenti scientifici che, basati su un’idea molto semplice, aprono nuovi ampi spazi all’esplorazione; oppure evidenziavano il ruolo dello sperimentatore, che è attivamente implicato nella realizzazione di qualcosa che non accade spontaneamente.

Nel valutare l’apparente semplicità degli esperimenti qui riportati, non bisogna ricavarne un’idea distorta. Spesso le dimostrazioni che riproducono un esperimento possono enormemente semplificare il processo sperimentale utilizzando moderni equipaggiamenti che hanno già in vista la “risposta giusta”. A questo proposito il professor Robert Crease, ideatore del sondaggio, scrive: “Anche quando un esperimento scientifico punta ad un fatto o ad una relazione semplice, normalmente è stato estratto da una ‘matrice di complessità’ e introduce nuove complessità nella scienza. L’esperimento scientifico non è la semplice illustrazione di una lezione già preparata, ma un processo tramite il quale una verità fino ad allora sconosciuta viene svelata per la prima volta”. Allora emerge il bello della scoperta.