Lisp »Tips 'n Tricks »QJS »1 »2

Un Quaternione è un insieme di Julia in 4 dimensioni.
La formula di Julia (z²+c) è la stessa, ma z e c sono numeri quaternioni.
Un numero quaternione ha un valore reale a₀ e 3 valori immaginari e si può esprimere con la notazione a₀+a₁i+a₂j+a₃k, dove i j e k sono vettori unitari (come l'immaginario i del numero complesso a₀+a₁i) in tre direzioni ortogonali perpendicolari all'asse reale.
La moltiplicazione di 2 q. segue le seguenti regole
i²=j²=k²=-1 ij=-ji=k jk=-kj=i ki=-ik=j (la moltiplicazione tra quaternioni è priva della proprietà commutativa).

Dato un numero Q (a,bi,cj,dk) la procedura per disegnare un QJS (Quaternion Julia Set) è un'estensione della procedura per disegnare un insieme di Julia con i numeri complessi *:
z²:
(a,bi)^2.reale = a*a-b*b
(a,bi)^2.immag(i)= 2*a*b
Q²:
(a,bi,cj,dk)^2.reale = a*a-b*b-c*c-d*d
(a,bi,cj,dk)^2.immag(i) = 2*a*b
(a,bi,cj,dk)^2.immag(j) = 2*a*c
(a,bi,cj,dk)^2.immag(k) = 2*a*d

(a,bi,cj,dk)^2=

=(a,bi,cj,dk)*(a,bi,cj,dk)

=a(a,bi,cj,dk)+bi(a,bi,cj,dk)+cj(a,bi,cj,dk)+dk(a,bi,cj,dk)

=(a^2+abi+acj+adk)+(bia+bi^2+bicj+bidk)+(cja+cjbi+cj^2+cjdk)+(dka+dkbi+dkcj+dk^2)

->i²=j²=k²=-1

=(a^2+abi+acj+adk)+(bia-b^2+bicj+bidk)+(cja+cjbi-c^2+cjdk)+(dka+dkbi+dkcj-d^2)

=(a^2-b^2-c^2-d^2)+abi+acj+adk+bia+bicj+bidk+cja+cjbi+cjdk+dka+dkbi+dkcj

=(a^2-b^2-c^2-d^2)+i(ab+ba)+j(ac+ca)+k(ad+da)+bcij+bdik+cbji+cdjk+dbki+dckj

=(a^2-b^2-c^2-d^2)+i(2ab)+j(2ac)+k(2ad)+bck-bdj-cbk+cdi+dbj-dci

=(a^2-b^2-c^2-d^2)+i(2ab)+j(2ac)+k(2ad)+k(bc-cb)+j(-bd+db)+i(cd-dc)

=(a^2-b^2-c^2-d^2)+i(2ab)+j(2ac)+k(2ad)+k*0+j*0+i*0

=(a^2-b^2-c^2-d^2)+i(2ab)+j(2ac)+k(2ad)

Q²+q è la formula implementata nel lisp (q è una costante, nel lisp espressa con i numeri reali cR, cI, cJ e cK, dove R sta per reale e c per costante) e il risultato è una sezione bidimensionale (a_x,a_y) nel piano selezionato (a_xx,a_yy) di un QJS. Nel lisp il piano è al livello costante di 0.05 ma può essere cambiato da input.

Selezione delle coppie di parametri costanti di Q:

 (1) [a  b] c   d
 (2) [a] b [c]  d
 (3) [a] b  c  [d]
 (4)  a [b  c]  d
 (5)  a [b] c  [d]
 (6)  a  b [c   d]

Il lisp disegna in nero l'insieme di punti contenuti nel quadrato |x|,|y| <= 2 la cui orbita non esce, prima di n iterazioni, dal cerchio con centro nell'origine e raggio 2. Inoltre |q|<=2.

QJ1

;|

    QJ1.LSP (C)2005 by Claudio Piccini
    www.cg-cad.com

    Quaternion Julia Sets 2D

|;

(defun qJs1 ( / m n i
                a b c d
                t0 t1 t2 t3
                l
 )
 (setq m 0)
 (while (< m dim)
  (setq n 0)
  (while (< n dim)
   (cond
    ((= tipoP 1) ; [a b] c d
     (setq a k1)
     (setq b k1)
     (setq c (+ -2 (/ (* m 4.0) dim)))
     (setq d (+ -2 (/ (* n 4.0) dim)))
    )
    ((= tipoP 2) ; [a] b [c] d
     (setq a k1)
     (setq b (+ -2 (/ (* m 4.0) dim)))
     (setq c k1)
     (setq d (+ -2 (/ (* n 4.0) dim)))
    )
    ((= tipoP 3) ; [a] b c [d]
     (setq a k1)
     (setq b (+ -2 (/ (* m 4.0) dim)))
     (setq c (+ -2 (/ (* n 4.0) dim)))
     (setq d k1)
    )
    ((= tipoP 4) ; a [b c] d
     (setq a (+ -2 (/ (* m 4.0) dim)))
     (setq b k1)
     (setq c k1)
     (setq d (+ -2 (/ (* n 4.0) dim)))
    )
    ((= tipoP 5) ; a [b] c [d]
     (setq a (+ -2 (/ (* m 4.0) dim)))
     (setq b k1)
     (setq c (+ -2 (/ (* n 4.0) dim)))
     (setq d k1)
    )
    ((= tipoP 6) ; a b [c d]
     (setq a (+ -2 (/ (* m 4.0) dim)))
     (setq b (+ -2 (/ (* n 4.0) dim)))
     (setq c k1)
     (setq d k1)
    )
   )
   (setq i 0)
   (while (< i steps)
    (setq i (1+ i))
    (setq t0 (+ (- (* a a)(* b b)(* c c)(* d d)) cR))
    (setq t1 (+ (* 2 a b) cI))
    (setq t2 (+ (* 2 a c) cJ))
    (setq t3 (+ (* 2 a d) cK))
    (setq a t0 b t1 c t2 d t3)
    (setq l (+ (* a a)(* b b)(* c c)(* d d)))
    (if (> l 2)(setq i steps))
   )
   (if (< l 2) 
    (command "_point" (list (+ m (car p0))(+ n (cadr p0))))
   )
   (setq n (1+ n))
  )
  (setq m (1+ m))
 )
)

(defun c:qj1 ( / snapp 
                 steps dim p0 K
                 cR cI cJ cK
                 tipoP k1
 )
 (setvar "cmdecho" 0)
 (setq snapp (getvar "osmode"))
 (command "_osnap" "_non")
 (princ "\nJulia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).")
 ;|
   Selezione delle coppie di parametri costanti di Q:
  1) [a  b] c   d 
  2) [a] b [c]  d
  3) [a] b  c  [d]
  4)  a [b  c]  d
  5)  a [b] c  [d]
  6)  a  b [c   d]
 |;
 (setq K 1)
 (while K
  (setq tipoP (getint "\nSelezione coppia parametri costanti di Q (1-6):"))
  (if (AND (> tipoP 0)(<= tipoP 6))(setq K nil))
 )   
 (setq k1 (getreal "\nValore parametro costante di Q [0.05]: "))
 (if (= k1 nil)(setq k1 0.05))
 (princ "\nValore parametri costante q=cR+cI+cJ+cK")
 (setq cR (getreal "\ncR [-0.745]: "))
 (if (= cR nil)(setq cR -0.745))
 (setq cI (getreal "\ncI [0.113]: "))
 (if (= cI nil)(setq cI 0.113))
 (setq cJ (getreal "\ncJ [0.01]: "))
 (if (= cJ nil)(setq cJ 0.01))
 (setq cK (getreal "\ncK [0.01]: "))
 (if (= cK nil)(setq cK 0.01))
 (initget (+ 2 4)) ; non 0 non negativo
 (setq steps (getint "\nSteps [100]: "))
 (if (= steps nil)(setq steps 100))
 (initget (+ 2 4)) ; non 0 non negativo
 (setq dim (getint "\nDimensione griglia frattale [200]: "))
 (if (= dim nil)(setq dim 200))
 (setq p0 (getpoint "\nSeleziona un punto del disegno..."))
 (qJs1)
 (setvar "osmode" snapp)
 (command "_redraw")
 (setvar "cmdecho" 1)
 (princ)
)
;;;eof

Test del Lisp

Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):1
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

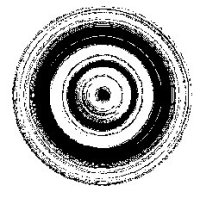
Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):2
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):3
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):4
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):5
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

Command: qj1
Julia di Q^2+q (Q=a0+a1+a2+a3, q=cR+cI+cJ+cK).
Selezione coppia parametri costanti di Q (1-6):6
Valore parametro costante di Q [0.05]: Invio
Valore parametri costante q=cR+cI+cJ+cK
cR [-0.745]: Invio
cI [0.113]: Invio
cJ [0.01]: Invio
cK [0.01]: Invio
Steps [100]: Invio
Dimensione griglia frattale [200]: 600
Seleziona un punto del disegno...

Per approfondire:

(*) C.A. Pickover, Computers, Pattern, Chaos and Beauty - 2001, Dover Publications, Inc.

(*) AutoLISP Tips & Tricks volume I. [36] Funzioni ricorsive § 7e VII

Ecco un generatore di insiemi di Julia complessi (che non fa uso di procedure ricorsive):

;;; julia.lsp (C)2005 by Claudio Piccini
;;; www.cg-cad.com

(defun fJulia ( / m n i 
                  x0 y0 x y x1 y1 
                  R
 )
 (setq m 0)
 (while (< m dim)
  (setq n 0)
  (while (< n dim)
   (setq x0 (+ -2 (/ (* m 4.0) dim)))
   (setq y0 (+ -2 (/ (* n 4.0) dim)))
   (setq x x0)
   (setq y y0)   
   (setq i 0)
   (while
    (progn
     (setq i (1+ i))
     (setq x1 (+ (- (* x x)(* y y)) cx))
     (setq y1 (+ (* 2 x y) cy))
     (setq x x1)
     (setq y y1)
     (setq R (+ (* x x)(* y y)))
     (if (> R 4)  nil T) 
     (if (< i 20) T nil)
    )
   )
   (if (< R 4)
    (command "_point" (list (+ m (car p0))(+ n (cadr p0))))
   )
   (setq n (1+ n))
  )
  (setq m (1+ m))
 )
)

(defun c:julia ( / snapp 
                   dim p0 
                   cx cy
 )
 (setvar "cmdecho" 0)
 (setq snapp (getvar "osmode"))
 (command "_osnap" "_non")
 (initget 1) ; non nil 
 (setq cx (getreal "\n parte reale di c: "))
 (initget 1) ; non nil 
 (setq cy (getreal "\n parte immag. di c: "))
 (initget (+ 2 4)) ; non 0, non negativo
 (setq dim (getint "\n lato griglia frattale [300]: "))
 (if (= dim nil)(setq dim 300))
 (setq p0 (getpoint "\n seleziona un punto nel disegno..."))
 (fJulia)
 (setvar "osmode" snapp)
 (command "_redraw")
 (setvar "cmdecho" 1)
 (princ)
)
;;;eof

Lisp »Tips 'n Tricks

Ultimo Aggiornamento_Last Update: 17 Maggio 2005