Cercando una soluzione all'equazione x²+1=0 e rinunciando alla struttura di ordine si ammette l'esistenza di un numero immaginario non reale i tale che i²=-1.

I nuovi numeri immaginari interagiscono con i numeri reali e con i risultati delle operazioni di addizione e moltiplicazione, ad esempio 1+3i²-2i³ e in generale il polinomio a₀+a₁i+a₂i²+...+a_niⁿ, con a₀,...a_n numeri reali.
Sostituendo i² con -1 si semplifica il polinomio nella forma x+iy dove x e y sono numeri reali.

Esempio:
1+3i²-2i³ = 1+3i²-2(i²)i = 1+3(-1)-2(-1)i = 1-3+2i = -2+2i.

x+iy è la forma canonica del numero complesso z (x si chiama parte reale e y parte immaginaria di z).

(1) I numeri complessi possono essere rappresentati da un punto in un piano complesso (x,iy) messo in rapporto con il piano cartesiano (x,y): il punto z=x+iy equivale al punto p(x,y).

Per definizione il modulo |x+iy| di un numero complesso z è la distanza del punto (x,y) dall'origine degli assi: |z|=(sqrt (x²+y²))
La distanza fra i punti che rappresentano numeri complessi è data dal modulo della loro differenza: |z'-z"|.

(2) Dalla definizione di modulo si ricava che l'insieme dei numeri complessi unitari (cioè numeri complessi di modulo = 1) è il cerchio con centro nell'origine e raggio 1.

Le operazioni fra numeri complessi sono analoghe alle operazioni algebriche fra binomi. La somma di due numeri complessi è un numero complesso che ha per parte reale x la somma delle parti reali e per parte immaginaria y la somma delle parti immaginarie.

Esempio:
(2+3i)+(4+6i)=(2+4)+(3+6)i=6+9i
La moltiplicazione di un mumero complesso per se stesso è:
(x+iy)(x+iy)=x²+ixy+ixy+i²y²=x²+i(2xy)+(-1)y²=x²-y²+i(2xy)

IQDR itera 100 volte la funzione di elevazione al quadrato di un numero complesso z².
f(z)=z² f(z)=f(x+iy)=x²-y²+(2xy)i
Da (1) si ottengono le coordinate x e y del punto (numero complesso) da iterare:
x = x²-y²
y = 2xy

;
; IQDR by Claudio Piccini
; (c)2004 (30 marzo 2004)
; www.cg-cad.com
; Itera la funzione complessa f(z)=z2
;

(defun c:iqdr ( / snapp 
                  K x0 y0 j x1 y1
 )
 (setvar "cmdecho" 0)
 (setq snapp (getvar "osmode"))
 (command "_osnap" "_non")
 (setq K 1)
 (while K
  (initget 1) ;non nil 
  (setq x0 
   (getreal "\nParte reale di z [-2<=x<=2]= ")
  )
  (if (and (>= x0 -2)(<= x0 2))
   (setq K nil)
  )
 )
 (setq K 1)
 (while K
  (initget 1) ;non nil 
  (setq y0 
   (getreal "\nParte immag. di z [-2<=y<=2]= ")
  )
  (if (and (>= y0 -2)(<= y0 2))
   (setq K nil)
  )
 )
 (setq j 1)
 (while (<= j 100)
  (command "_point" (list x0 y0))
  (setq x1 (- (* x0 x0)(* y0 y0)))
  (setq y1 (* 2 x0 y0))
  (setq x0 x1)
  (setq y0 y1)
  (setq j (1+ j))
 )
 (setvar "osmode" snapp)
 (command "_redraw")
 (setvar "cmdecho" 1)
 (princ)
)
;eof

Test del LISP

Command: iqdr
Parte reale di z [-2<=x<=2]= 0.5
Parte immag. di z [-2<=y<=2]= 0.8

(sqrt (0.5²+0.8²)) = (sqrt (0.25+0.64)) = (sqrt 0.89) < 1

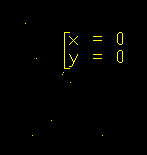Orbita di z² con numero complesso = 0.5+0.8i
Le orbite dei punti tendono al punto fisso 0

Command: iqdr
Parte reale di z [-2<=x<=2]= 0.61
Parte immag. di z [-2<=y<=2]= 0.8

(sqrt (0.61²+0.8²)) = (sqrt (0.3721+0.64)) = (sqrt 1.0121) > 1

Orbita di z² con numero complesso = 0.61+0.8i (particolare)
Le orbite dei punti tendono a ∞

Command: iqdr
Parte reale di z [-2<=x<=2]= 0.6
Parte immag. di z [-2<=y<=2]= 0.8

(sqrt (0.6²+0.8²)) = (sqrt (0.36+0.64)) = (sqrt 1) = 1
Dal punto (2) si evince che tutti i punti dovrebbero stare sulla circonferenza di raggio 1 ma minimi errori numerici introdotti ad ogni iterazione spingono le orbite al centro o all'infinito (è l'effetto farfalla di E. Lorenz, cioè la dipendenza critica dalle condizioni iniziali, ingrediente essenziale di un sistema caotico come ad esempio il tempo atmosferico).

Orbita di z² con numero complesso = 0.6+0.8i (particolare)
Clicca sull'immagine per ingrandire.

L'insieme dei punti che stanno sulla circonferenza è detto insieme di Julia di f(z)=z²: Julia è il confine fra le orbite che tendono al punto fisso 0 e quelle che fuggono all'infinito.

In generale l'insieme di Julia è l'insieme delle orbite instabili di un sistema dinamico complesso.

Per approfondire:
Caos e frattali, R.L. Devaney. Editore Addison-Wesley Masson

Ultimo Aggiornamento_Last Update: 4 Aprile 2004