Si intende indicare elementari dimostrazioni di asserzioni che solitamente, nell’insegnamento della matematica nella scuola media, vengono fornite allo studente come corredo nozionistico utile a svolgere argomenti di maggiore utilità.

A chiarimento si può fare riferimento alle operazioni con le frazioni che richiedono il calcolo del minimo comune multiplo e quindi la scomposizione in fattori che richiede la conoscenza dei criteri di divisibilità:questi vengono suggeriti come regole da ritenere a memoria. Anche nello studio delle frazioni generatrici di numeri periodici vengono fornite le regole senza alcuna spiegazione.

Si inizia proprio con questi due argomenti e si forniscono elementari dimostrazioni.

CRITERI DI DIVISIBILITA'

Divisibilità per 3 e per 9

Sia x = un numero intero. Ci proponiamo di determinare le condizioni perché esso sia divisibile per 3(o per 9).

Scriviamo il numero dato in forma decimale :

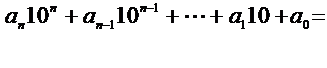
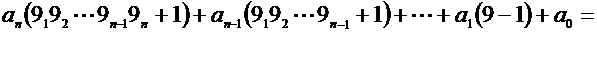
Poiché i primi n addendi sono divisibili per 3 e per9, x sarà divisibile per 3 e/o per 9 se e solo se lo sarà la somma delle cifre costituenti il numero dato.

Divisibilità per 4.

Consideriamo:

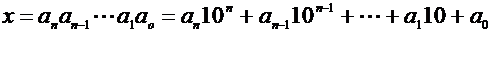
Poiché i primi n-1 addendi sono divisibili per 4, x sarà divisibile per 4 se e solo se è divisibile per 4 il numero costituito dalle ultime due cifre del numero dato.

Divisibilità per 7

Consideriamo il numero x scritto in forma decimale x = a₀ + a₁10 + a₂10² +

Le successive potenze di 10 divise per 7 ripetono periodicamente la stessa sequenza:

1, 3, 2,-1,-3,-2.

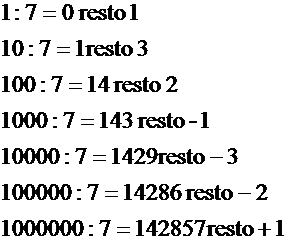
Dunque x è divisibile per 7 se e solo se

a₀ +3a₁ + 2a₂ - a₃ - 3a₄ - 2a₅ + a₆ + 3a₇ + 2a₈ - ...

= (a₀ - a₃ + a₆- ...) +3(a₁-a₄ + a₇ - ...) +2(a₂ - a₅ + a₈- ...) risulta divisibile per 7.

Criterio di divisibilità di un numero dato per un qualsiasi numero d.

Siano r₀, r₁, r₂, ... i resti della divisione di 10⁰, 10¹, 10², ... per d.

Dette a₀, a₁, a₂, ..., a_n le cifre di x, risulta che il numero dato è divisibile per d se e solo se

r₀a₀ + r₁a₁ + r₂a₂ + ... + r_na_n

è divisibile per d.

La successione dei resti è sicuramente periodica, dato che i resti non nulli della divisione per d possono essere al più d - 1, e si possono quindi raggruppare opportunamente le cifre

Esempio- Criterio di divisibilità per 11

Sia x un numero in forma decimale;

le successive potenze di 10 divise per 11 danno per resti alternativamente 1e -1:

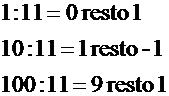
Ne consegue che x sarà divisibile per11 se e solo se lo sarà la somma, in valore assoluto, delle sue cifre prese alternativamente con il segno + e con il segno -.