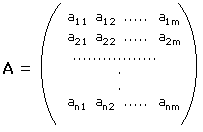
Lezione del 16/5/2001
Una successione {ak} finita (cioè il cui massimo indice n è un numero finito) viene anche chiamato vettore. I singoli termini della successione sono le componenti del vettore. In questo caso si usa la notazione a = (a1,a2,...,an). Un vettore uk di componenti tutte nulle tranne una di valore unitario, ad esempio u3 = (0,0,1,0,...,0), viene chiamato versore. Si adotterà la convenzione di indicare un vettore con una lettera in grassetto.
Prodotto scalare fra vettori: ab = a1b1 + a2b2 +...+ anbn.
Due vettori a e b sono ortogonali se ab = 0. Versori diversi, uj e uk, sono ortogonali.
I versori godono anche della proprietà ujuk = 1 se j = k. Pertanto ak = auk.
Quando si parlerà di polinomi ortogonali e di analisi di Fourier si vedrà che tali proprietà possono essere estese a successioni di funzioni.
Una successione bidimensionale finita {ajk} è chiamata matrice. Si usa scrivere una matrice disponendo i suoi elementi in uno schema rettangolare; in questo caso l'indice j assume il nome di indice riga mentre k è l'indice colonna. Ad es., una matrice n x m si indica nel modo seguente
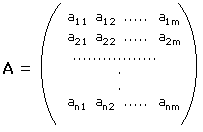
Un vettore può essere considerato, indifferentemente, come una matrice formata da una sola riga (vettore riga) o una sola colonna (vettore colonna).
Date due matrici A e B entrambe n x m,
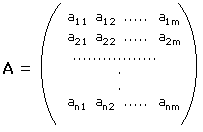 |
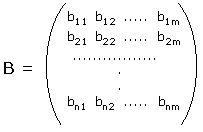 |
si definisce l'operazione di somma fra matrici nel seguente modo
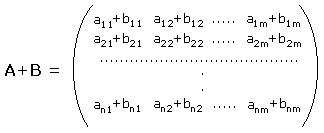
Si definisce il prodotto fra le matrici A e B, una n x p e l'altra p x m, come il prodotto fra le righe di A per le colonne di B; ogni elemento della matrice sarà formato dal prodotto scalare dei vettori riga di A per i vettori colonna di B. La sua dimensione sarà n x m.
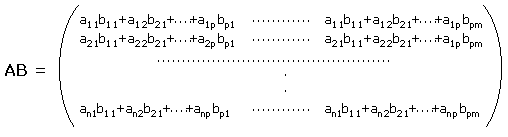
Dato un vettore colonna x = (x1,x2,...,xm), il risultato del prodotto Ax con la matrice A,di dimensione n x m, sarà il vettore colonna y = (y1,y2,...,yn). Per esercizio provare a dimostrarlo.
Scambiando righe con colonne della matrice A otteniamo la cosiddetta matrice trasposta At che avrà la seguente struttura
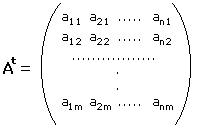
Se il numero di righe è uguale a quello delle colonne cioè n = m, si parla di matrici quadrate.
In una matrice quadrata si definisce diagonale principale il vettore formato dagli elementi che hanno l'indice riga e colonna uguali, ovvero d = (a11,a22,...,ann).
Particolare importanza hanno le seguenti matrici quadrate
| Matrice triangolare (alta) | Matrice diagonale | Matrice unità |
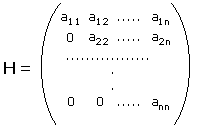 |
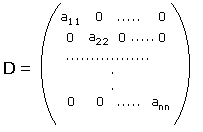 |
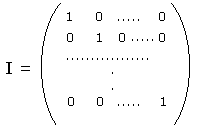 |
E' facile verificare perché la terza viene chiamata in quel modo...
Schemi di permutazione bidimensionale
Possono essere definite per le matrici le stesse operazioni combinatorie su successioni finite unidimensionali (vettori).
Un quadrato latino è una matrice quadrata di ordine n le cui righe e colonne sono formate da permutazioni di n elementi:
|
E' facile verificare che la somma degli elementi di ogni riga o colonna è costante ed è uguale a 10.
- Vettori
- Matrici
- Matrici particolari
- Permutazioni a 2 dimensioni
Pagina iniziale ____________ Informatica e Telematica____________ Programma ____________ Bibliografia