Informatica e Telematica
Algoritmi
Ricordare che...
- Qualsiasi azione complessa può essere scomposta in una sequenza
di azioni elementari.
- La sequenza di passi che deriva dall'analisi di un
problema viene chiamata algoritmo se: 1) è ordinata; 2) descrive
il problema in maniera generale; 3) è convergente
(cioè ha un inizio e una fine)
Esercizi (Algoritmi)
Descrivere le seguenti azioni in maniera algoritmica:
- La preparazione di un piatto di spaghetti
- La salita al terzo piano di uno stabile tramite ascensore
- Accensione e partenza di un veicolo a motore
- Dal letto al posto di lavoro (o a scuola)
- La risoluzione di un'equazione di primo grado
- La scrittura di uno score o un instrument
per il sistema Csound
- La stesura manuale di un documento
Rappresentazione di algoritmi e
strutture fondamentali
Ricordare che...
- Gli algoritmi possono essere descritti utilizzando vari
metodi; alcuni tra i più semplici sono: lista lineare a passi numerati oppure il diagramma
di flusso (flow-chart).
- Il diagramma di flusso è una modalità di
rappresentazione grafica degli algoritmi; ogni passo è racchiuso in una box
ed è collegato al successivo tramite una freccia. La forma della box definisce
il tipo di azione elementare da svolgere (che da ora in poi chiameremo istruzione).
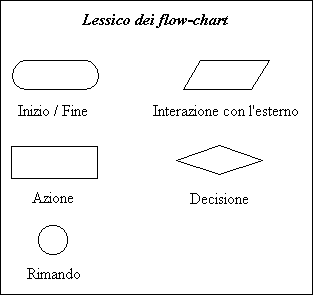
- I simboli grafici fondamentali, ovvero i tipi diversi di
istruzione sono, in realtà pochissimi: ne possiamo individuare 5 (v. figura)
____________________________ 
- Il flow-chart, nonostante la sua semplicità e
concisione, è un metodo di rappresentazione formale; ciò significa che, anche in
presenza di algoritmi banali, va tutto descritto con la massima precisione e in maniera
assolutamente univoca (cioè non deve esistere la possibilità di equivocare il
significato delle descrizioni).
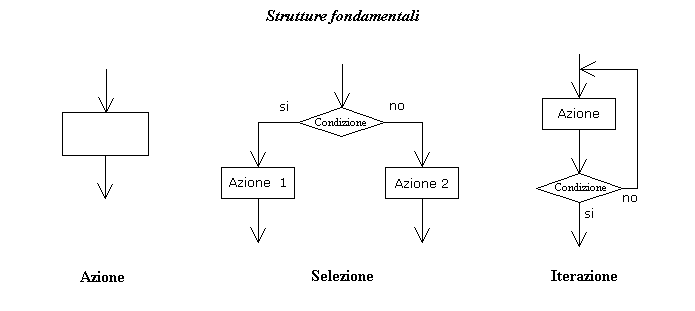
- Per rendere ancora più rigorosa la rappresentazione degli
algoritmi sono state definite le strutture fondamentali della
programmazione che sono: azione, selezione,
iterazione; è stato dimostrato matematicamente che tramite
queste sole 3 strutture è possibile descrivere qualsiasi algoritmo. Con la selezione è
possibile scegliere l'esecuzione di un'istruzione piuttosto che un'altra in dipendenza da
una condizione logica. Con un'iterazione possiamo ripetere un
gruppo di istruzioni finché non si verifica una condizione logica (che viene chiamata condizione
di fine ciclo)
___ 
- Una variabile, indicata con un simbolo
(ad es. sono simboli validi a, cont, indice), è un contenitore per valori di tipo diverso (ad es. numeri). A
una variabile può essere attribuito un valore tramite l'istruzione di assegnazione
(che, nei flow-chart, si indica con
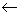 )
)
- Possiamo definire alcune variabili con funzioni
specifiche; ad es., un accumulatore è una variabile che si usa in questa
maniera: a
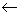 a + b in cui a rappresenta l'accumulatore e b è un numero qualsiasi: il significato di questa istruzione è
che ad a sarà
assegnato il valore che è contenuto in a in quel momento sommato al valore contenuto nella variabile b. Un contatore
è un caso particolare dell'accumulatore in cui b è uguale a 1. Accumulatori e contatori, di norma, vanno inizializzati:
prima di usarli all'interno di una struttura iterativa bisogna assegnare ad essi un valore
di partenza.
a + b in cui a rappresenta l'accumulatore e b è un numero qualsiasi: il significato di questa istruzione è
che ad a sarà
assegnato il valore che è contenuto in a in quel momento sommato al valore contenuto nella variabile b. Un contatore
è un caso particolare dell'accumulatore in cui b è uguale a 1. Accumulatori e contatori, di norma, vanno inizializzati:
prima di usarli all'interno di una struttura iterativa bisogna assegnare ad essi un valore
di partenza.
Esercizi (Algoritmi)
- Provare a descrivere tramite il flow-chart
i semplici algoritmi del paragrafo precedente
- Realizzare e descrivere con flow-chart
gli algoritmi relativi ai seguenti problemi:
- Moltiplicazione con somme iterate (completo della
trattazione del caso che almeno uno dei due operandi sia nullo)
- Elevazione a potenza tramite moltiplicazioni iterate
(completo dei casi particolari)
- Scambio dei valori contenuti in due variabili x e y
- Media di due numeri
- Introduzione di 20 numeri dall'esterno (input)
e calcolo, man mano che si introducono, del totale
- Introduzione di 15 numeri positivi e
ricerca del più piccolo fra essi
Prima della fine di ognuno degli
algoritmi inserire l'istruzione di visualizzazione del risultato.
Numerazione e aritmetica binaria.
Logica booleana
Chiarimenti sugli esercizi (Algoritmi) del precedente paragrafo
- (Realizzare e descrivere con flow-chart gli
algoritmi relativi ai seguenti problemi):
- Moltiplicazione con somme iterate
(completo della trattazione del caso che almeno uno dei due operandi sia nullo)
- Elevazione a potenza tramite moltiplicazioni
iterate (completo dei casi particolari)
- Scambio dei valori contenuti in due variabili x e y: ad esempio la variabile x contiene 5 e la y contiene 7;
scambiare i loro valori significa che, alla fine del procedimento, x deve contenere 7 e y deve contenere 5. Occorre una variabile di appoggio che serve a memorizzare il
contenuto di una delle 2 variabili prima di copiare in questa il valore dell'altra.
- Media di due numeri:
bisogna introdurre dall'esterno 2 valori in altrettante variabili (ad es. x e y), sommare i loro valori e dividere il risultato
per 2. Si può realizzare l'algoritmo anche usando una sola variabile.
- Introduzione di 20 numeri
dall'esterno (input) e calcolo, man mano che si introducono, del totale:
occorrono 3 variabili: una, che chiameremo acc, per il calcolo
del totale progressivo, l'altra, che chiameremo x, per l'ingresso dei
valori dall'esterno e, infine, un contatore, cont, che parte da 0 e
arriva a 20; ad ogni iterazione introduciamo dall'esterno un valore in x, accumuliamo x in acc, incrementiamo cont e verifichiamo se quest'ultimo è arrivato a 20 nel qual caso terminiamo
l'iterazione e visualizziamo il risultato.
- Introduzione di 15 numeri positivi
e ricerca del più piccolo fra essi: per questo algoritmo occorrono 3 variabili:
una, x, per l'ingresso dei valori, un contatore, cont, che assumerà valori da da 0 a 15, una variabile d'appoggio, min, per memorizzare il valore minimo che troviamo man mano che procede
l'elaborazione; prima della partenza dell'iterazione si inizializza la variabile min a 0 (il più piccolo valore positivo); a ogni iterazione si introduce un
valore positivo in x e se questo è minore di quello contenuto in min si effettua lo scambio fra min e x, in ogni caso si incrementa cont e se questo è
arrivato a 15 termina l'iterazione dopodiché si visualizzerà il risultato.
Numeri binari
- Le macchine di calcolo elettroniche eseguono le loro
operazioni su informazioni di natura binaria che è, poi,
l'unica forma di codifica che possono trattare; pertanto: qualsiasi elaborazione
compiuta da un calcolatore elettronico viene condotta sicuramente su numeri binari
- Come nella notazione decimale (in base 10), che ci è
familiare, abbiamo 10 cifre elementari con le quali possiamo comporre qualsiasi numero
usando il sistema posizionale (cioè l'importanza di una cifra dipende dalla sua
posizione: più è situata a sinistra più è "pesante"), così nel sistema
binario (in base 2) abbiamo solo 2 cifre elementari (dette bit)
con le quali comporre, sempre secondo il sistema posizionale, tutti i numeri. Il numero di
configurazioni binarie ottenibili con un insieme di n bit è 2n (ad es., con 4
bit si possono rappresentare 24=16 numeri e il più grande di questi è 2n-1 ovvero 24-1=15)
- La "sostanza" del sistema posizionale si può
esprimere con la seguente formula:
____________________ x=cn-1bn-1
+ cn-2bn-2 + .... + c1b1 + c0b0 ______________ (1)
per un numero x di n cifre ck espresso nella base b; se b=10 abbiamo la consueta
rappresentazione decimale (ad es., 137=1*102
+ 3*101 + 7*100); se b=2 saremo in
presenza di un numero binario (le cifre ck sono i bit) e la
precedente formula ci permette di conoscere il valore decimale di un numero binario; ad
esempio, il numero binario 10011101 (un numero a 8 bit come questo viene chiamato byte)
può essere scritto come: 1*27
+ 0*26 + 0*25 + 1*24 + 1*23 + 1*22
+ 0*21 + 1*20 = 157
- Nel punto precedente abbiamo elaborato un metodo per
conoscre il valore decimale di un numero binario. Può essere utile trovare un metodo per
eseguire la trasformazione inversa: dato un numero decimale calcolare il suo equivalente
binario. A questo scopo osserviamo che, eseguendo la divisione intera per b sul numero x della
formula (1), otterremo: x1=x/b=cn-1bn-2
+ cn-2bn-3 + .... + c1 con il resto c0 (che è la prima cifra binaria da destra); dividendo x1
per b avremo x2=x1/b=cn-1bn-2
+ cn-2bn-3 + .... + c2 con resto c1 e così via fino a che non avremo xn=0 con resto cn-1 che era l'ultima cifra binaria da trovare.
- Abbiamo detto che i calcolatori elettronici comprendono
solo informazioni espresse in termini di numeri binari. Sorge quindi il problema del
trattamento di quantità numeriche binarie con segno; in decimale possiamo usare, oltre le
usuali cifre numeriche, i segni + e - indicare se il numero è positivo o negativo. In
binario non abbiamo questa possibilità e, quindi, anche il segno dovrà essere codificato
con un bit. La codifica di numeri binari relativi più usata è la notazione
complemento a 2 a n bit; questa forma di rappresentazione nasce dalla
constatazione che, quando i numeri sono elaborati con un'aritmetica di lunghezza finita
(quando, cioè, il numero di bit usati per rappresentare un valore non può superare n), scrivere x-x=0 o x+x'=2n è equivalente (infatti per rappresentare 2n occorrerebbe
un'altra cifra oltre le n ammesse; ad es., 24 in base 2 è 10000 di cui
prendiamo solo le 4 cifre meno significative se la rappresentazione
binaria è a 4 bit): questo significa che, in un ambito binario di lunghezza finita, il
numero -x è equivalente al numero x'=2n-x.
- Dalle considerazioni svolte nel punto precedente ed
eseguendo qualche esperimento, possiamo affermare che in notazione complemento a 2 a n bit
si può distinguere un numero positivo da uno negativo osservando il bit più
significativo (quello più a sinistra): se questo ha valore 0 allora il numero è
positivo mentre, se è uguale a 1 è negativo.
- Un metodo pratico per invertire il segno di un numero
relativo binario è il seguente: invertire il valore di ogni bit del numero (tutti i bit a
0 diventano 1 e viceversa) e sommare al risultato 1; ad esempio, se vogliamo invertire il
segno del numero negativo a 8 bit 11011011 (-37 in decimale) avremo, applicando il precedente algoritmo, 00100101
(provare per credere...)
- Un problema che si può sorgere quando si eseguono calcoli
con un'aritmetica di lunghezza finita è l'overflow; questo si
può verificare quando, sommando due numeri positivi, otteniamo un risultato negativo e
viceversa. Ciò accade perché l'ambito numerico è limitato a n bit mentre il risultato
dell'operazione che ha provocato l'overflow ne richiederebbe di più.
- Una regola pratica per effettuare la somma fra 2 bit: 0+0=0, 0+1=1, 1+0=1, 1+1=0 con il riporto di 1 e, quindi, 1+1=10.
- Una maniera comoda e compatta di visualizzare un numero
binario è la notazione esadecimale (cioè in base 16). In questa forma
di rappresentazione ogni insieme di 4 bit si traduce in una cifra esadecimale (infatti con
4 bit si codificano i numeri da 0 a 15); per queste ultime si usano le stesse cifre
decimali da 0 a 9 con l'aggiunta delle lettere dell'alfabeto da A a F (oltre le
10 cifre decimali ne occorrono altre 6 per avere le 16 cifre esadecimali); ad es., il
numero binario 10011010 può essere scritto, in base 16, 9A (1001=9, 1010=10 (in
decimale) =A (in esadecimale)). Per indicare che il numero è notato in base 16 si usa
porre usa porre una 'h' (dall'inglese Hexadecimal) dopo di esso: l'esempio
precedente diventa 9Ah.
- Dato che i computer comprendono solo informazioni
rappresentate tramite i soli 2 bit 0 e 1, anche i dati non numerici dovranno essere
codificati in binario; ad esempio i caratteri alfabetici, segni di punteggiatura, simboli
speciali, etc. sono rappresentabili tramite lo standard ASCII (American
Standard Code for Interchange Information)
nato per la trasmissione di messaggi tra terminali remoti e calcolatori centrali
su linea telefonica. il codice ASCII (esteso) è costituito da 256 configurazioni binarie
(è un codice a 8 bit) adatti a rappresentare tutti i simboli che si usano nelle lingue
occidentali (che fanno uso dell'alfabeto latino) e che normalmente si trovano sulle
tastiere delle macchine da scrivere. Per fare qualche esempio, il carattere 'A' è
codificato, in ASCII, come 01000001 (41h), il carattere ';' come 00111011 (3Bh), il
carattere '7' come 00110111 (37h), il carattere 'a' come 01100001 (61h), etc.
- Sui numeri binari possono essere effettuate altre
operazioni oltre le consuete di somma/sottrazione e moltiplicazione/divisione; esistono,
ad esempio, le operazioni logiche come la AND, la OR
la XOR e la NOT (tanto per citare le più importanti).
Le prime tre devono avere almeno due operandi, mentre la quarta solo uno; il risultato che
si ottiene applicando un operatore logico su insiemi di bit è definito in una tabella
relativa all'operatore stesso e che si chiama tabella di verità. Ad es.,
le tabelle di verità dei 4 operatori citati sono visibili nella figura sottostante dove
con A e B si indicano i bit su cui sarà effettuata
l'operazione mentre con R si denota il risultato
| AND |
____ |
____ |
___________ |
OR |
____ |
____ |
___________ |
XOR |
____ |
____ |
___________ |
NOT |
____ |
| A |
B |
R |
|
A |
B |
R |
|
A |
B |
R |
|
A |
R |
| 0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
0 |
0 |
|
0 |
1 |
| 0 |
1 |
0 |
|
0 |
1 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
| 1 |
0 |
0 |
|
1 |
0 |
1 |
|
1 |
0 |
1 |
|
|
|
| 1 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
0 |
|
|
|
Consultando queste tabelle possiamo calcolare, ad esempio, 1001 AND 0111 applicando
l'operatore logico AND bit per bit e ottenendo 0001; oppure possiamo calcolare 1010 XOR 1111 = 0101, etc. Esiste poi l'operazione di shift (a destra
e a sinistra) che consiste nello spostare di un certo numero di posti (a destra o a
sinistra) i bit che compongono un numero binario; quest'operatore si indica con il simbolo
>> (shift a destra) o con << (shift a sinistra). Ad esempio,
10111101>>2 = 00101111, mentre 01011010<<4=10100000 (i posti lasciati vuoti dai bit uscenti sono, di norma, riempiti
con 0).
- Lo shift a destra corrisponde a una divisione per
una potenza di 2, quello a sinistra a un'analoga moltiplicazione. Dagli esempi del punto
precedente, 10111101>>2 =
00101111 corrisponde alla divisione
del numero per 22 mentre 01011010<<4=10100000 corrispone all moltiplicazione per 24.
- Per poter elaborare numeri con virgola si usa la notazione
floating-point che consiste nel rappresentare il valore numerico
come una coppia formata da una mantissa (che è la parte strettamente
numerica e deve essere compresa, in decimale, tra 0 e 1) ed esponente
(che invece dà una misura dell'entità del numero); il numero risultante da questa coppia
è mbe dove m è la mantissa, b è la base in cui è rappresentato
il numero (quindi 2 se binario), e è l'esponente; mantissa ed esponente sono entrambi relativi
(complemento a 2).
- Per eseguire la somma tra due numeri floating-point
è necessario eguagliare gli esponenti (aumentando il minore dei due) ed effettuando le
opportune compensazioni sulla mantissa; a questo punto basta sommare le due mantisse così
manipolate per ottenere il risultato. La moltiplicazione, invece, consiste nell'esecuzione
del prodotto fra le mantisse e della somma degli esponenti. Ad esempio, (01001100;0010)+(01110101;0000)=(01001100;0010)+(00011101;0010)=(01101001;0010) osservando che aumentando l'esponente del secondo operando di 2
unità (da 0000 a 0010) devo dividere la mantissa per 22 (cioè devo
effettuare uno shift a destra di 2 posti) cioè per la base in cui è
rappresentato il numero elevata al numero di incrementi dell'esponente.
Esercizi (Rappresentazione
dei dati)
- Esercizi sui numeri binari ed esadecimali
- Qual'è il campo numerico rappresentabile
con 12, 16 e 32 bit?
- Dati i seguenti numeri binari,
trasformarli in numeri decimali: 10011100,
1111001111, 10100101, 10001001, 11110110
- Dati i seguenti numeri decimali,
trasformarli in binario: 123, 511,
760, 381, 587, 1015
- Sommare le seguenti coppie di numeri
binari:
011111111010 + 010100001011 ;
111110100000 + 000110101000 ; 10101011110011010000 + 11001010111111111110
- Trasformare in decimale relativo i
seguenti numeri negativi espressi in notazione complemento a 2:
10001111, 11111111, 10000000, 11100001, 10100101, 10110110
- Date le seguenti coppie di numeri binari
relativi (in notazione complemento a 2 a 8 bit), eseguire la loro somma commentando
brevemente ogni risultato (che dovrà essere sempre a 8 bit) :
01010010 + 00111011 ; 01110110 + 01101111 ; 10001111 + 11000101 ; 10100101 + 01011010
- Sommare le seguenti coppie di numeri
espressi in notazione esadecimale e trasformare in binario il risultato: 7FA + 50B ; FA0 + 1A8 ; BABA + CAFFE
- Eseguire le seguenti operazioni floating-point:
(11001010; 0011) + (01000110; 0101)
(11000000; 0111) + (01011010; 0010)
(01100011; 0011) * (01001111; 0100)
- Eseguire le seguenti operazioni logiche:
10110011 AND 00001111; 00001001 OR 01100000; 11010111 XOR 00010000.
- Descrivere in forma algoritmica i metodi di
passaggio da numeri in base 10 a base 2 e viceversa
Tabelle di traccia
Uso delle tabelle di traccia: prendiamo
in esame il flow-chart relativo all'esercizio n.3 del 28/2 (scambio dei valori
contenuti in due variabili)
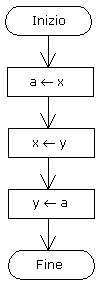
La tabella di traccia si costruisce ponendo
sulle colonne le variabili di cui si vuole studiare il comportamento e sulle righe i
valori che assumono tali variabili ogni volta che avanza il processo. Ad esempio abbiamo
supposto che alla partenza x contenga il valore 5 e y il valore 7; la tabella
di traccia sarà
Variabile |
| a |
x |
y |
| - |
5 |
7 |
| 5 |
5 |
7 |
| 5 |
7 |
7 |
| 5 |
7 |
5 |
|
_____
_____
Inizializzazione
dopo la 1. istruzione
dopo la 2. istruzione
dopo la 3. istruzione |
Conviene sempre compilare una tabella di traccia per ogni
algoritmo sviluppato (quando ciò è possibile) in modo da verificare la correttezza della
soluzione trovata.
Pagina iniziale ________________ Matematica ________________ Programma ________________ Bibliografia



