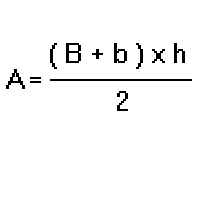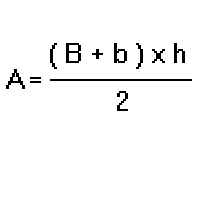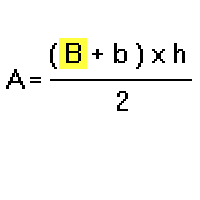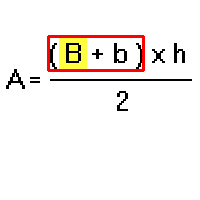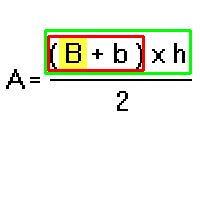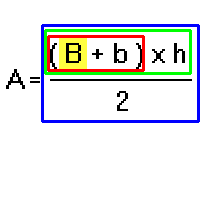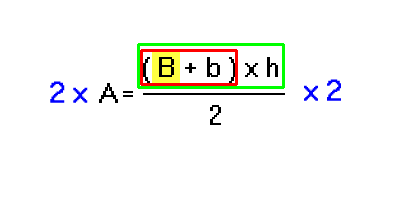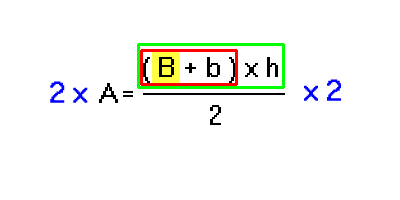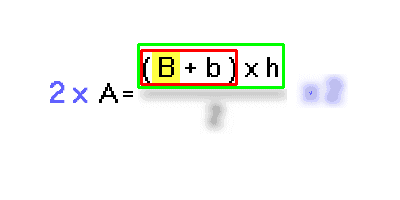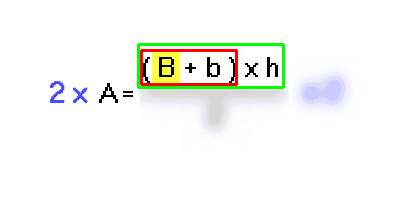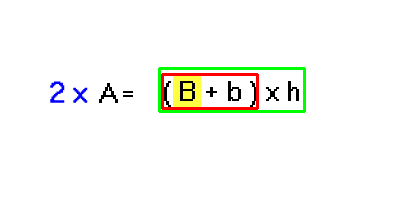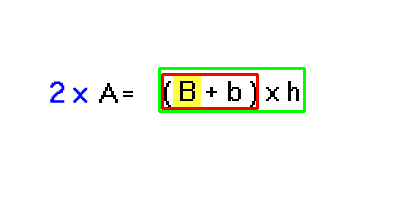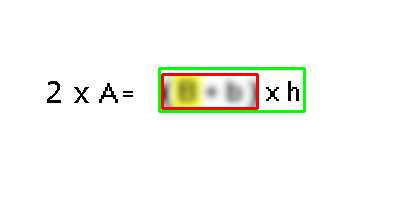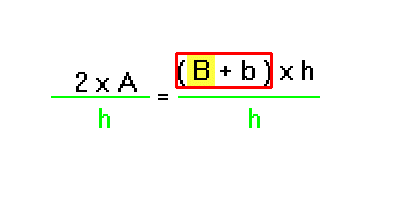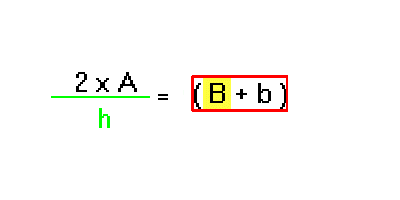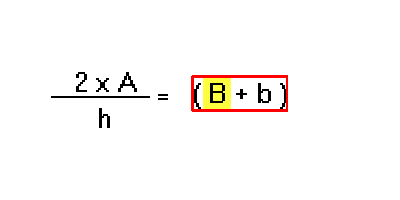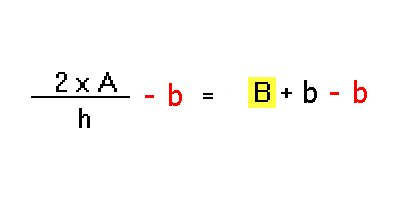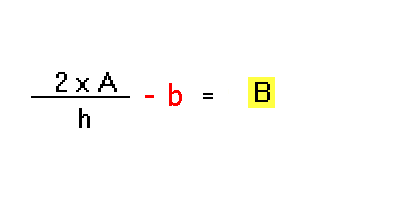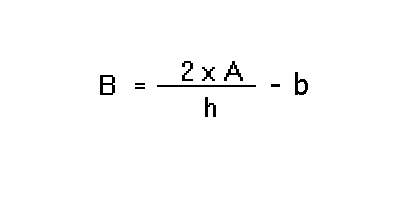Formule inverse a partire da un esempio
Data la formula per il calcolo dell'Area di un trapezio:
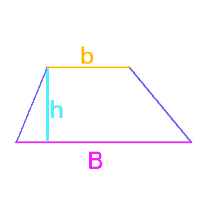
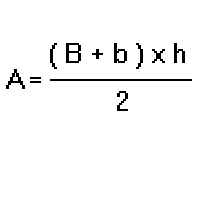in cui
A = AREA
B = Base Maggiore
b = base minore
h = altezza
Sono noti i seguenti dati:
A
b
h
Si vuole ricavare il valore di B
Passo 1.
Identificare e evidenziare quello che cerchiamo, cioè B
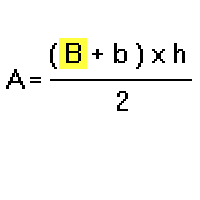
Passo 2.
Quello che cerchiamo, B, non è libero. E' bloccato da alcune operazioni.
Quali?
Cerchiamo l'operazione più vicina a B: è una somma (B + b); riquadriamola: abbiamo la scatola 1 - somma di b.
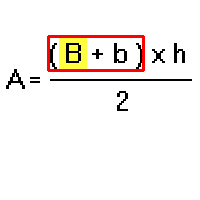
Passo 3.
Questa somma, a sua volta, è bloccata da un'altra operazione, una moltiplicazione: (B + b) x h; riquadriamo anche questa: è la scatola 2 - moltiplicazione per h.
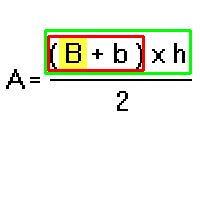
Passo 4.
Anche questa moltiplicazione è invischiata in un'altra operazione, una divisione: (B + b) x h / 2; tracciamo un ultimo riquadro: è la scatola 3 - divisione mediante 2.
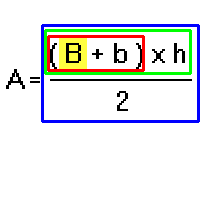
Tutti questi riquadri sono paragonabili alle matrioske, le bamboline russe, o alle scatole cinesi: non è possibile giungere alla più interna senza aprire le altre, partendo dalla più esterna.
IMPORTANTE: Ogni scatola ha una sua serratura.
Passo 5.
Apro la scatola più esterna. Per aprire questa scatola serve una chiave.
La chiave è l'operazione inversa: per aprire la scatola 3 - divisione mediante 2 serve una chiave moltiplicazione per 2
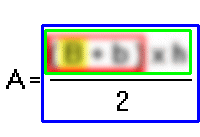
Ma l'uguaglianza pretende che
QUELLO CHE SI FA DA UNA PARTE
SI FACCIA ANCHE DALL'ALTRA DEL SEGNO DI =.
(La chiave funziona così: per aprire la scatola esegue la stessa operazione sui 2 membri dell'uguaglianza).
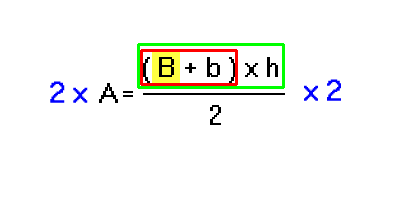Si avrà la semplificazione nel membro a destra del segno di =
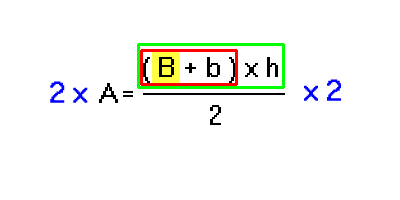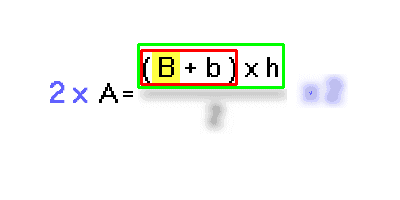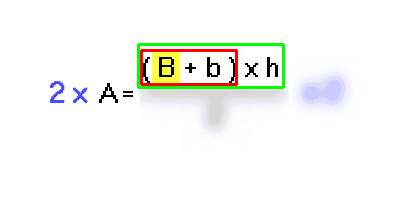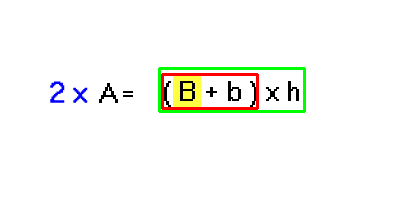
Si ottiene in tal modo:
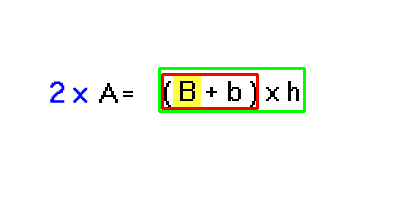
Ora bisogna ripetere il passo 5 per togliersi dai piedi la moltiplicazione. Quindi ....
Passo 6.
Apro di nuovo la scatola più esterna. Anche per aprire questa scatola serve una chiave.
La chiave è la nuova operazione inversa: per aprire la scatola 2 - moltiplicazione per h serve una chiave divisione mediante h
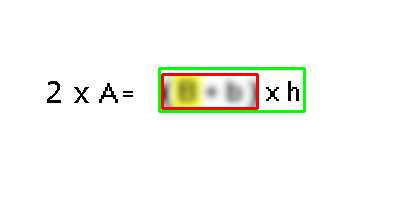
Ma, di nuovo, l'uguaglianza pretende che
QUELLO CHE SI FA DA UNA PARTE
SI FACCIA ANCHE DALL'ALTRA DEL SEGNO DI =.
(Anche questa chiave funziona così: per aprire la scatola esegue la stessa operazione sui 2 membri dell'uguaglianza).
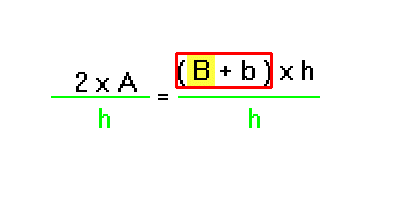Si avrà la semplificazione nel membro a destra del segno di =
Si ottiene in tal modo:
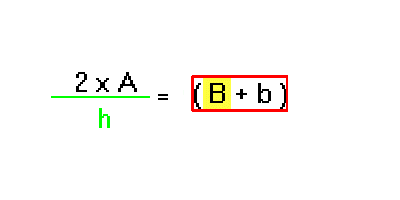
Ora bisogna ripetere il passo 6 per togliersi dai piedi la somma. Perciò ....
Passo 7.
Apro l'ultima scatola. Anche per aprire questa scatola serve la sua chiave.
La chiave è (l'avresti detto?) la nuova operazione inversa: per aprire la scatola 1 - somma di b serve una chiave sottrazione di b
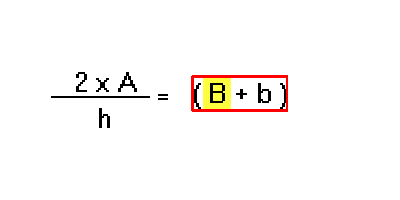
Ma, di nuovo, l'uguaglianza pretende che
QUELLO CHE SI FA DA UNA PARTE
SI FACCIA ANCHE DALL'ALTRA DEL SEGNO DI =.
(Anche questa chiave funziona così: per aprire la scatola esegue la stessa operazione sui 2 membri dell'uguaglianza).
Una precisazione: le parentesi non servono più, quindi sono state tolte.
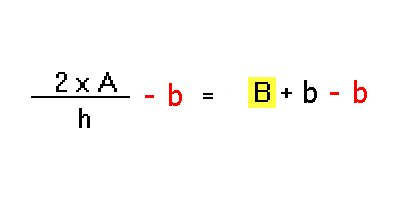Si avrà la semplificazione nel membro a destra del segno di =
Si ottiene in tal modo:
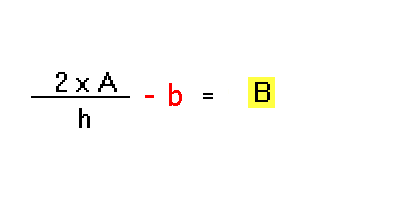Adesso, come dicono i matematici puristi, per la proprietà simmetrica, posso scambiare di posto i 2 membri.
In altre parole posso leggere prima il secondo membro e poi il primo e ottengo:
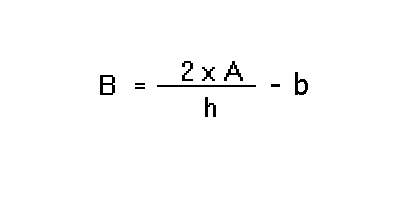
E COSI' SONO ARRIVATO IN FONDO: HO "FATTO" LA FORMULA INVERSA, RICAVANDO QUELLO CHE MI INTERESSAVA
Se vuoi, puoi prelevare un file compresso (forinv.zip di circa 90 kB), che contiene questo file htm e i file grafici a lui collegati, cliccando qui.
Potrai quindi scompattarli in una cartella del tuo computer e visualizzarli off-line.
Copyleft: Questo file è a disposizione di tutti. E' prelevabile, stampabile, copiabile, riproducibile, ecc.
Si prega cortesemente di citare l'autore.
Chiunque voglia mi può comunicare miglioramenti da apportare e critiche: non mi offendo.
Grazie davvero a chi contribuirà a rendere queste paginette realmente utili a tutti quelli che ne hanno bisogno. Gigi
Numero download: 105,224
Autore: Gigi Oliva - Genova - 15 maggio 2006 - Ultima modifica: 17 maggio 2006