Una semplice costruzione geometrica e due luoghi dalle equazioni complicate
In questa pagina, scritta in collaborazione con il collega Daniele Bellio (liceo scientifico G. Marconi di Conegliano Veneto), presentiamo una semplice costruzione geometrica riguardante la suddivisione di un triangolo in coppie di triangoli aventi il medesimo perimetro. Successivamente, con alcune ipotesi semplificatrici e con l'aiuto di software geometrico forniamo la visualizzazione del luogo di alcuni punti coinvolti nella costruzione. Infine, sfruttando le capacità simboliche di Mathematica, deduciamo la complicata rappresentazione parametrica di questi luoghi.
Dato un triangolo ABC, siano a, b, c le misure dei lati opposti rispettivamente ai vertici A, B, C; su ogni lato del triangolo esiste un punto tale che il segmento che lo congiunge con il vertice opposto divide il triangolo dato in due triangoli con lo stesso perimetro (isoperimetrici). Determinare tali punti e alcune delle loro proprietà.
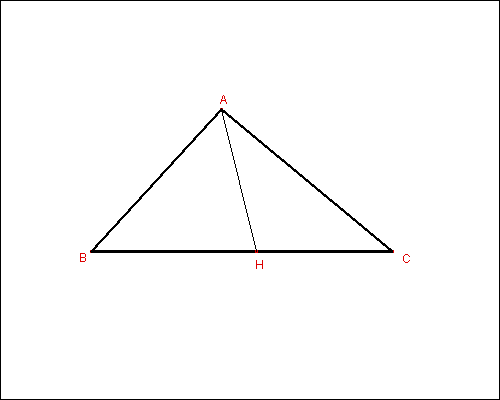
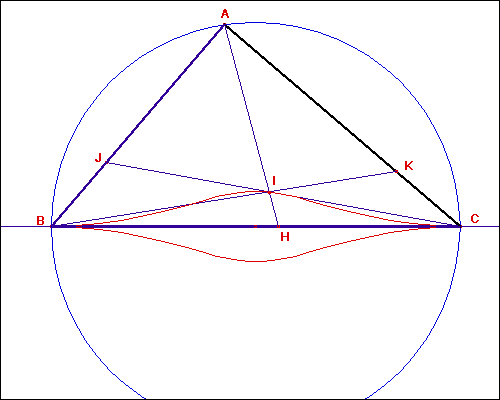
Consideriamo il triangolo ABC (fig. 1):
vogliamo determinare il punto H del lato BC tale che i triangoli ABH e AHC abbiano il medesimo perimetro. Poiché tale richiesta si traduce nella relazione
| AB + BH + HA | = | AC + CH + HA |
e osservato come il segmento AH (che, "in letteratura", viene detto lo splitter del triangolo) sia comune ai due triangoli ABH e AHC, discende che dev'essere pure
| AB + BH | = | AC + CH. | (1) |
Per costruire H, tracciamo la circonferenza di centro B e raggio AB (fig. 2):
questa interseca la retta contenente BC dalla parte di B, nel punto D. Allo stesso modo, la circonferenza di centro C e raggio AC interseca la retta BC (dalla parte di C) in E. Dato che DB = AB e AC = EC, la relazione AB + BH = AC + CH si riscrive come
| DB | + | BH | = | EC | + | CH | ossia | DH | = | EH. |
Il punto cercato H dev'essere pertanto il punto medio del segmento DE. Ciò risolve il problema in quanto è elementare ottenere il punto medio di DE.
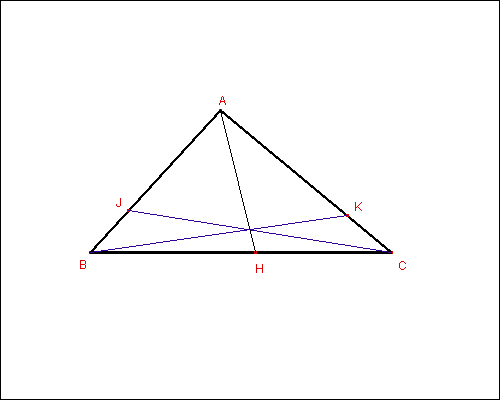
Ripetendo la costruzione sui rimanenti lati si determinano facilmente gli ulteriori punti J, K (fig. 3).
Proprietà
Vediamo di dedurre qualche proprietà di questa costruzione. Poiché il perimetro 2p di ![]() ABC risulta
ABC risulta
| AB | + | BH | + | AC | + | CH | = | 2p | = | a | + | b | + | c |
per l'uguaglianza (1) questa relazione si può scrivere come
| AB | + | BH | + | (AB + BH) | = | 2 | (AB + BH) | = | 2p |
da cui discende AB + BH = p ossia
| BH | = | p - c. | (2a) |
Allo stesso modo valgono le seguenti espressioni
| HC | = | p - b | KC | = | p - a | AK | = | p - c | AJ | = | p - b | BJ | = | p - a | (2b) |
Ne segue una prima importante proprietà: i punti H, J, K suddividono i lati in coppie di segmenti congruenti: nello specifico abbiamo
| BH | = | AK | HC | = | AJ | KC | = | BJ. |
Inoltre le relazioni (2a, b) sono le stesse di quelle definite in un triangolo dai punti di tangenza delle circonferenze ex-inscritte con ciascun lato del triangolo e ciò suggerisce che le due terne di punti siano in realtà coincidenti.
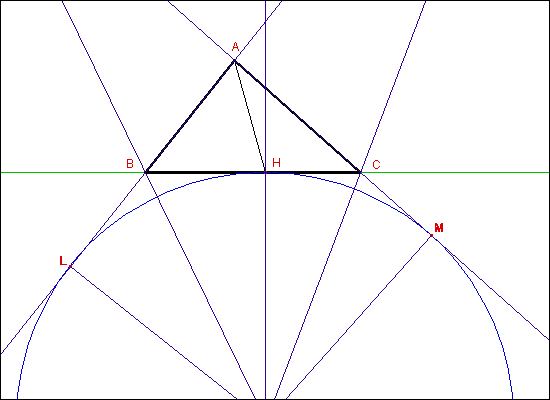
Difatti, sia O il centro della circonferenza ex-inscritta a ![]() ABC, tangente al lato BC nel punto H1 e ai prolungamenti di AB e AC rispettivamente in L e M (fig. 4).
ABC, tangente al lato BC nel punto H1 e ai prolungamenti di AB e AC rispettivamente in L e M (fig. 4).
Poiché A è un punto esterno alla circonferenza e AB e AC sono le tangenti condotte da questo punto alla medesima circonferenza è immediato dedurre
| AL | = | AM. |
Riscritta quest'ultima come
| AB | + | BL | = | AC | + | CM |
e notato che, per lo stesso teorema, risulta
| BL | = | BH1 | CM | = | CH1 |
si ha subito
| AB | + | BH1 | = | AC | + | CH1 |
relazione che mostra come il punto di tangenza H1 possieda la medesima proprietà di H dato che soddisfa alla stessa relazione (1). È immediato ora dedurre, nello stesso modo seguito inizialmente, che BH1= p - c e quindi, in base all'unicità del punto avente una determinata distanza da un estremo di un segmento, concludere che H = H1.
Non appena si siano costruiti i tre punti H, J, K e i segmenti AH, CJ e BK (fig. 3), la figura suggerisce la congettura che i tre segmenti concorrano tutti in uno stesso punto che, in tal caso, verrebbe a costituire un punto notevole del triangolo. In effetti tale congettura può essere dimostrata rigorosamente in base al teorema di Ceva inverso che afferma:
- Teorema di G. Ceva inverso
- Se tre rette ceviane AH, BK, CJ passanti per i vertici di un triangolo ABC e secanti i lati in H, K, J, suddividono i lati in coppie di segmenti BH e HC, CK e KA, AJ e JB, tali che
allora le tre rette concorrono in uno stesso punto I.BH
HC· CK
KA· AJ
JB= 1,
Anche in tal caso la dimostrazione segue immediata: è sufficiente sostituire a primo membro dell'uguaglianza i valori, precedentemente trovati, per i suddetti segmenti
| (p - c) (p - b) |
· | (p - a) (p - c) |
· | (p - b) (p - a) |
= | 1. |
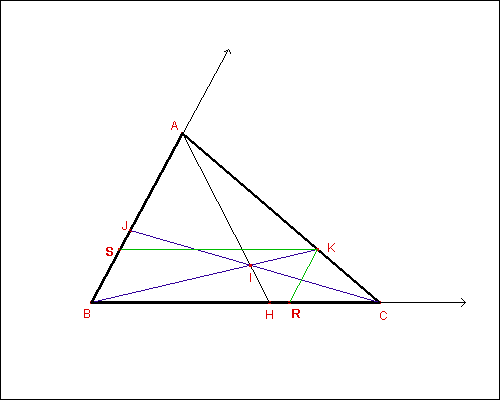
Tale proprietà potrà anche essere dimostrata, per esempio, per via analitica. Fissiamo quindi un sistema di riferimento con assi obliqui aventi origine in B e assi lungo le rette dei lati AB e BC (fig. 5).
Con tale scelta le coordinate dei punti coinvolti discendono immediatamente da quanto finora discusso e sono
| A(0,c), | B(0,0), | C(a,0), | J(0, p-a), | H(p-c, 0), |
mentre quelle del punto K si deducono non appena, tracciate le parallele KR e KS agli assi, si noti la similitudine tra il triangolo originario ![]() ABC e
ABC e ![]() ASK ossia
ASK ossia
| SK AK |
= | BC AC |
: | sostituendo si ottiene | SK p - c |
= | a b |
da cui discende l'ascissa xK di K cioè
| SK | = | BR | = | xK | = | a(p - c) b | . |
Sfruttando la similitudine tra ![]() ABC e
ABC e ![]() KRC si ottiene l'altra coordinata
KRC si ottiene l'altra coordinata
| RK KC |
= | AB AC |
RK p - a |
= | c b |
da cui
| RK | = | BS | = | yK | = | c(p - a) b | . |
Le equazioni delle tre rette ceviane si ottengono nel sistema obliquo allo stesso modo che in un sistema ortogonale ossia sfruttando la formula
| y - y1 | = | y2 - y1 x2 - x1 |
· | (x - x1) |
cosicché giungiamo alle espressioni
| retta BK | : | y | = | c(p - a) a(p - c) |
x |
| retta CJ | : | y | = | p - a -a |
(x - a) |
| retta AH | : | y - c | = | c -(p - c) |
x. |
Poiché la risoluzione dei tre sistemi formati dalle tre possibili coppie di queste rette fornisce in ogni caso sempre il punto di coordinate
| x | = | a(p - c) p |
y | = | c(p - a) p |
le tre rette devono essere concorrenti. Il punto che queste rette ceviane definiscono viene detto punto di Nagel del triangolo (punto che nei testi specialistici viene indicato con N o Na).
I luoghi dei punti I, J, K
L'esistenza di un punto notevole suscita la curiosità di investigare sulla sua "variabilità" in varie specie di triangoli, dovendo comunque vincolare in qualche modo il triangolo di partenza. Una scelta immediata è quella relativa al caso di un triangolo rettangolo con vertice (retto) in A e quindi inscritto in una semicirconferenza di diametro BC: studieremo quindi il luogo di I al variare di A sulla semicirconferenza stessa. Osserviamo al contempo il luogo descritto dagli altri due punti J, K mentre H descrive, naturalmente, il diametro della semicirconferenza.
Lo studio con Cabri del luogo del punto I fornisce la risposta riportata sotto (fig. 6) dove, per simmetria il vertice A viene fatto variare sull'intera circonferenza di diametro BC.
Analogamente, al variare di A sulla circonferenza i punti J e K appartengono ai luoghi mostrati dalla figura successiva (fig. 7).
Tali luoghi stimolano pure la ricerca delle loro equazioni rappresentative magari per poter eventualmente trovare analogie con curve celebri già studiate in passato. Nel seguito cercheremo perciò di sfruttare le proprietà simboliche di Mathematica per ottenere una rappresentazione parametrica di questi luoghi.
Analisi dei luoghi dei punti J e K tramite Mathematica
Cerchiamo di costruire, tramite Mathematica, una rappresentazione parametrica dei luoghi ottenuti sopra con Cabri. A tal fine, inserita la circonferenza di raggio unitario nel sistema cartesiano di origine O di fig. 8,
appare naturale porre l'angolo AOC = α come il parametro che determina la posizione del vertice A. Sarà in funzione di questo parametro che determineremo le equazioni dei luoghi.
Le coordinate dei vertici di ![]() ABC sono (cominciamo da questo punto ad utilizzare la sintassi tipica di Mathematica)
ABC sono (cominciamo da questo punto ad utilizzare la sintassi tipica di Mathematica)
pA = {Cos[α], Sin[α]};
pB = {-1, 0};
pC = {1, 0};
Utilizzando un approccio che fa uso del calcolo vettoriale, definiamo i vettori
BA = pA - pB; CA = pA - pC; BJ = k BA; CK = h CA;
dove BJ e CK sono espressi in termini dei parametri incogniti k e h. Lo scopo è di determinare tali parametri al fine di dedurre le posizioni di J e K. Poiché scalarmente
| BJ + BC | = | CA + AJ |
esprimiamo tale relazione con i vettori definiti sopra considerando che BC = 2 e, vettorialmente AJ = BJ - BA (rappresentiamo i vettori con simboli in grassetto).
equaz1 = Sqrt[BJ.BJ] + 2 == Sqrt[CA.CA] + Sqrt[(BJ - BA).(BJ - BA)]
Otteniamo come output l'equazione nell'incognita k
Risolvendo tale equazione in k si ottengono le due soluzioni
soluzioniParamk = k /. Solve[equaz1, k] // Simplify

Ne segue che, considerando il primo valore (volendo J interno a BA), il vettore BJ possiede componenti
BJ = soluzioniParamk[[1]] BA

Le coordinate di J nel sistema cartesiano sono quindi espresse dal vettore OJ ossia
OB = {-1, 0};
OJ = OB + BJ

Queste coordinate forniscono, al variare di α, la rappresentazione parametrica cercata del luogo dei punti J. Il grafico della corrispondente funzione parametrica risulta, per α compreso nell'intervallo [0,2π]
ParametricPlot[OJ, {α, 0, 2π}, AspectRatio -> Automatic, Ticks -> {{-1, -.8, -.7}, Automatic}];

che coincide con quanto si ottiene in Cabri. Per il punto K ci aspettiamo un luogo simmetrico rispetto all'asse y a quello appena determinato e la procedura è la medesima. Dato che
| BC + CK | = | BA + AK |
e osservato che AK = CK - CA, i comandi sinteticamente sono:
equaz2 = Sqrt[CK.CK] + 2 == Sqrt[BA.BA] + Sqrt[(CK - CA).(CK - CA)] soluzioniParamh = h /. Solve[equaz2, h] // Simplify CK = soluzioniParamh[[1]] CA
Le coordinate di K sono quindi date da OK
OC = {1, 0};
OK = OC + CK
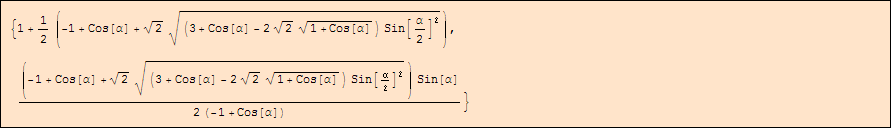
Infine l'unione dei due luoghi per i punti J e K
ParametricPlot[{OJ, OK}, {α, 0, 2π}, AspectRatio -> Automatic];

conferma quanto ottenuto in Cabri.
Luogo dei punti I
Passiamo ora al calcolo delle coordinate del punto I intersezione dei segmenti BK e CJ. Procederemo ancora in forma vettoriale definendo i vettori BI e CI in termini dei parametri incogniti m e n
BK = OK + {1, 0};
CJ = OJ - {1, 0};
BI = m BK;
CI = n CJ;
Imponendo la relazione vettoriale tra i lati di un triangolo
| BI + IC + CB | = | 0 |
e risolvendo il sistema in due incognite che ne deriva dovendo annullare ciascuna componente, si ottengono le non semplici espressioni
valoriParametri = Solve[BI - CI + {-2, 0} == {0, 0}, {m, n}] // Simplify

Esplicitando solo il parametro n
n = n /. valoriParametri
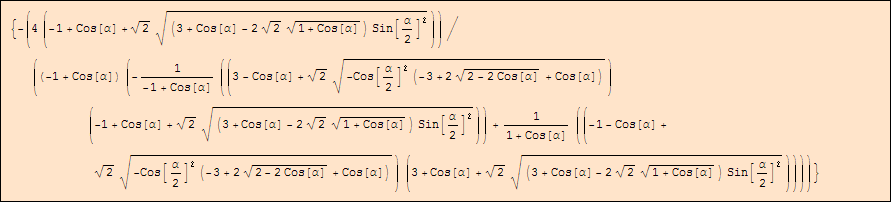
otteniamo infine le coordinate del punto I determinando le componenti del vettore OI = OC + CI
OI = Flatten[CI + {1, 0}]

L'espressione ottenuta costituisce pure la rappresentazione parametrica del luogo cercato. In conclusione, il grafico del luogo dei punti I al variare del parametro α tra 0 e 2π risulta
ParametricPlot[OI, {α, 0, 2π}, AspectRatio -> Automatic, PlotRange -> {{-1.1, 1.1}, {-0.2, 0.2}}];
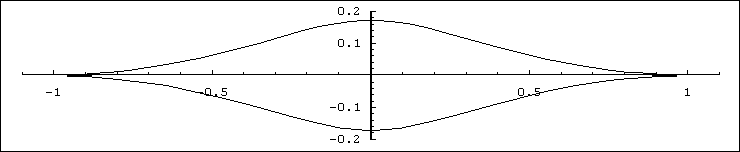
Questo grafico, a parte la complicata espressione della forma parametrica cui siamo giunti, conferma in modo sintetico quanto aspettato e ottenuto per altra via con Cabri.
Istruzioni per il prelievo
Nella riquadro sottostante si può prelevare il file zip contenente tutto il necessario per la consultazione off-line di questa pagina.