Iperbole: costruzione n. 4

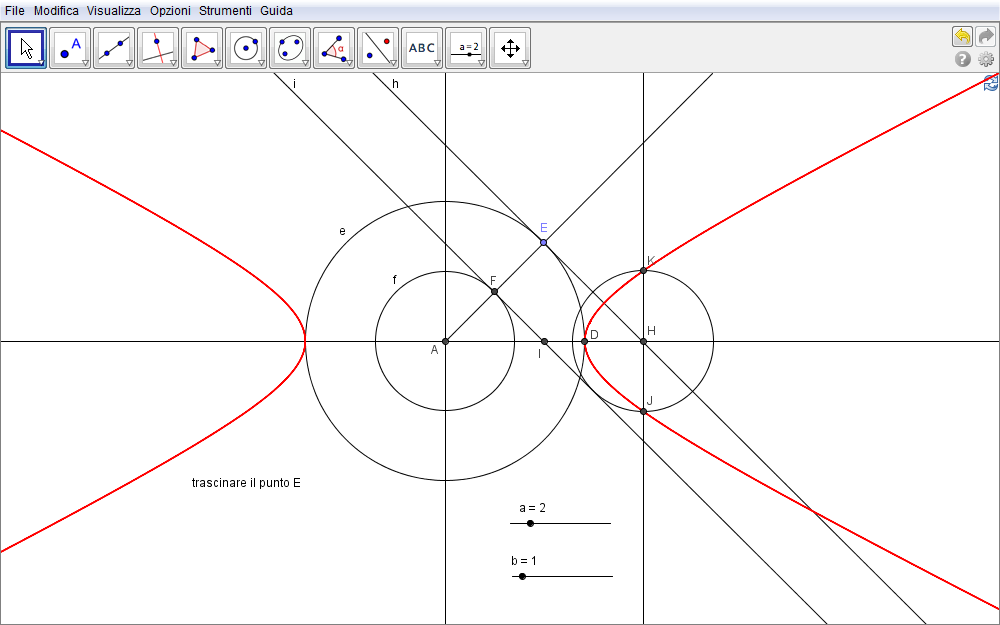
La costruzione qui proposta (fig. 3.10) parte dalla conoscenza delle lunghezze dei due semiassi. Sia quindi a la lunghezza del semiasse focale o trasverso e b quella dell'asse ad esso perpendicolare. Entrambi i valori saranno rappresentati nella costruzione da due slider. Pertanto,

• definiti gli slider a e b variabili nell'intervallo [0,10],
• tracciamo due rette c e d mutuamente perpendicolari nel punto A.
• Quindi, con lo strumento Circonferenza-dati centro e raggio, tracciamo una circonferenza e di centro A e raggio a
• ed una seconda f con lo stesso centro e raggio b.
• Definito un punto E sulla prima circonferenza,
• sia g la semiretta di origine A per E
• e F l'intersezione di questa con la seconda circonferenza.
• Disegniamo quindi le rette tangenti h e i alle due circonferenze, rispettivamente nei punti E ed F.
• Le retta h incontra la retta c in H mentre
• la retta i interseca c nel punto I.
• Tracciata la perpendicolare j a c per H,
• con lo strumento Compasso disegniamo la circonferenza di centro H e raggio pari alla lunghezza del segmento FI.
• I punti J e K di intersezione di quest'ultima circonferenza con la retta j sono i punti dell'iperbole cercata: per una prima conferma visiva è sufficiente chiedere la visualizzazione con
• lo strumento Luogo per J e K al variare di E sulla circonferenza e.

Figura 3.10. iperbole10.ggb.

Deduzione dell'equazione canonica e rappresentazione parametrica

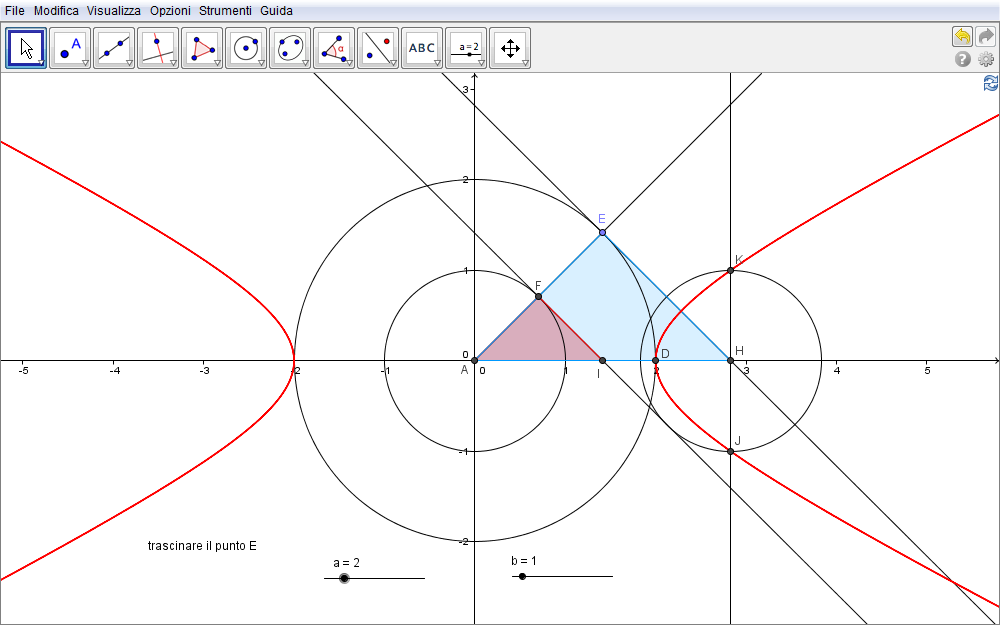
La costruzione sopra permette di giungere facilmente all'equazione canonica dell'iperbole ma soprattutto ad una sua rappresentazione parametrica.

Figura 3.11. iperbole11.ggb.

Difatti, sulla base della similitudine dei triangoli rettangoli $\triangle AIF\sim\triangle AHE$ (fig. 3.11), possiamo scrivere la proporzione $$\begin{equation}{AI\over AF}={AH\over AE}\quad\Rightarrow\quad {AI\over b}={AH\over a}\end{equation}$$ essendo $AE=a$ e $AF=b$. Ne deriva che $$\begin{equation}AI={b\over a}AH.\label{eq:2}\end{equation}$$ D'altra parte il teorema di Pitagora applicato a $\triangle AIF$ fornisce pure $$\begin{equation}AI^2=AF^2+FI^2=b^2+FI^2\label{eq:3}\end{equation}$$ per cui inserendo la $\eqref{eq:2}$ in quest'ultima, abbiamo $$\begin{equation}\biggl({b\over a}AH\biggr)^{\kern-2pt 2}\!=b^2+FI^2.\label{eq:4}\end{equation}$$ Se ora associamo alle originarie rette perpendicolari, c e d, gli assi di un sistema cartesiano di origine $A$ (fig. 3.11), risulta che l'ascissa dei punti $K$ e $J$ è $AH=x$ mentre il valore assoluto delle rispettive ordinate è rappresentato dalle lunghezze dei segmenti $HK=HJ=\bigl|\,y\,\bigr|$. Poiché per costruzione $HK=FI$ è pure $FI=\bigl|\,y\,\bigr|$ e l'equazione $\eqref{eq:4}$ diviene $$\begin{equation}\biggl({b\over a}x\biggr)^{\kern-2pt 2}\!=b^2+y^2.\end{equation}$$ Svolto il quadrato e diviso per $b^2$ ne deriva l'equazione canonica $$\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{{x^2\over a^2}-{y^2\over b^2}=1.}\end{equation}$$

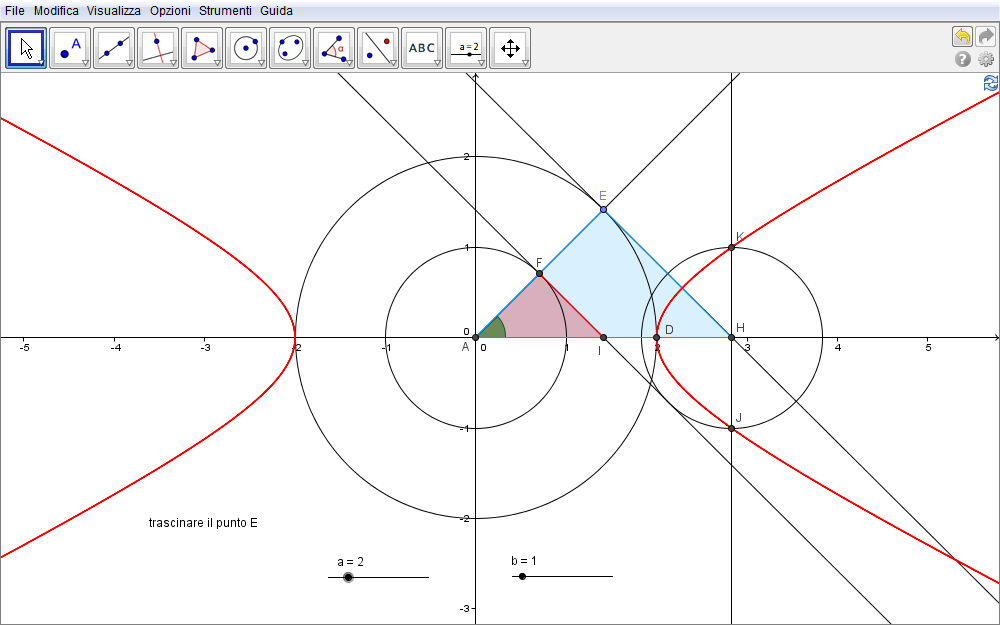
Per dedurre una rappresentazione parametrica dell'iperbole introduciamo l'angolo $\alpha=\angle\,DAE$ (fig. 3.12) che, affinché la costruzione abbia significato, deve soddisfare alla condizione $\alpha\not=\bigl\{\pm{\pi\over 2}\bigr\}$.

Figura 3.12. iperbole12.ggb.

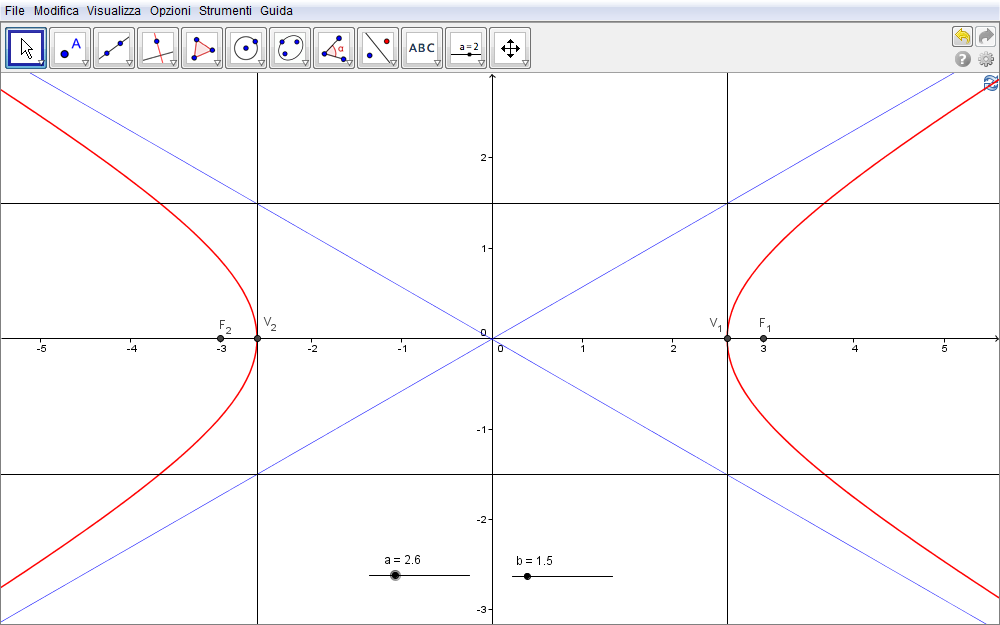
Poiché $$\begin{equation}{FI\over AF}=\tan\alpha\end{equation}$$ dato che $\triangle AIF$ è retto in $F$ e, come detto $FI=y$, risulta $$\begin{equation}{y\over b}=\tan\alpha\quad\Rightarrow\quad y=b\tan\alpha.\end{equation}$$ Per l'ascissa $x=AH$ osserviamo che in $\triangle AHE$ $$\begin{equation}{AE\over AH}=\cos\alpha\end{equation}$$ per cui $$\begin{equation}{a\over AH}= \cos\alpha\quad\Rightarrow\quad AH=x={a\over\cos\alpha}.\end{equation}$$ Se infine ricordiamo la definizione di secante, $\sec\alpha=1\,/\cos\alpha$, la rappresentazione parametrica cui siamo giunti si può riassumere nelle equazioni $$\begin{equation}\bbox[border:1px solid red,15px,#ffffcc]{\cases{x={a\over\cos\alpha}=a\sec\alpha\cr \cr y=b\tan\alpha.\cr}}\end{equation}$$ Nella figura 3.13 che segue abbiamo riportato la coppia di equazioni parametriche utilizzando il comando Curva[]: in particolare il comando inserito dalla barra è Curva[a sec(α), b tan(α),α,-π/2,π/2]. Abbiamo inoltre aggiunto, sempre dalla barra di inserimento $$\begin{equation}\hbox{gli asintoti}\ \ y=\pm{b\over a}x,\qquad \hbox{le rette}\ \ y=\pm\, b,\ x=\pm\, a,\qquad\hbox{i vertici}\ \ V(\pm\, a,0),\qquad \hbox{e i fuochi}\ \ F(\pm\sqrt{a^2+b^2},0)\end{equation}$$ grandezze tutte dipendenti dalle lunghezze dei semiassi $a$ e $b$ rappresentati dai corrispondenti slider.

Figura 3.13. iperbole13.ggb.